23

2.2. Пассивный эксперимент: общая характеристика

Предположим, что на объекте проведен пассивный эксперимент. Результаты эксперимента образуют конечную выборку (табл.2.1).

При проведении пассивного эксперимента соблюдались следующие условия:

- входные параметры x1 , x2 ,...xn измеряются с пренебрежимо малыми ошибками,

-появление ошибки в определении y объясняется наличием в процессе невыявленных переменных,

-найденные по наблюдениям значения y1, y2 ,...yN отвечают нор-

мальному закону распределения, т.е. выходная координата объекта обладает свойствами дискретной случайной величины.

Определение 2 [6 ]

Случайная дискретная величина (Y) – это такая величина, точное значение которой в предстоящем измерении предсказать невозможно.

Для анализа дискретных случайных величин используют ряд характеристик: математическое ожидание (MY), дисперсию (DY), среднее квадратическое отклонение (СКО), законы распределения.

Математическое ожидание (MY) случайной величины Y характеризует среднее значение этой величины:

где N – число событий (измерений), Yi – значение случайной величины Y, P(Yi ) – вероятность события (случайная величина Y имеет значение Yi).

Дисперсия случайной величины DY – характеризует степень рассеивания Y относительно MY:

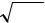
Среднее квадратическое отклонение (СКО) случайной величины

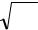
24

Исчерпывающей вероятностной характеристикой дискретной случайной величины Y является закон распределения, который обычно задается в виде функции распределения P(y).

Дискретное распределение считается заданным, если известны все возможные значения y1, y2 ,...yN , принимаемые случайной величиной, и ве-

роятности (P(yi) для каждого такого события (Y=yi). Причем ∑p( yi ) = 1.

i

Существуют различные законы распределения: нормальный, равномерный, Пуассона, экспоненциальный и др. Эмпирический (экспериментальный) график распределения случайной величины называется гистограммой.

Вся совокупность значений, которые может принимать случайная величина Y={yi}, образует генеральную совокупность значений.

В технических задачах обычно имеют дело с ограниченным числом из-

мерений Y ={y1 , y2 ,...yN }, с так называемой конечной выборкой.

Характеристики случайной величины (MY), (DY), (СКО), законы распределения определяют по генеральной совокупности значений Y. По конечной выборке можно найти только оценки характеристик случайной величины.

Оценка для математического ожидания случайной величины Y:

Оценка среднеквадратического отклонения (СКО) случайной величины

Формулы (2.4) – (2.6) позволяют найти так называемые точечные оценки математического ожидания, дисперсии и СКО. Каждая оценка должна удовлетворять ряду требований:

1) оценка должна быть состоятельной, т.е. с увеличением числа измерений N оценка my должна сходиться по вероятности к соответствующему параметру (характеристике) генеральной совокупности:

25

2) оценка должна быть несмещенной, т.е. она не должна содержать систематических (в среднем) отклонений:

3) оценка должна быть эффективной , т.е. в среднем иметь минималь-

Оценки, найденные по формулам (2.4) – (2.6), являются состоятельными, несмещенными и эффективными.

Интервальные оценки характеристик случайной величины позволяют определить вероятность того, что отклонение оценки my от истинного

значения MY будет не меньше заданной величины.

Для определения близости оценки к оцениваемому параметру вводят доверительный интервал близости ε, а саму близость оценивают по величине вероятности Р, которую называют доверительной вероятностью β и задают заранее (Р = β).

Таким образом, задача оценки состоит в том, чтобы выбрать или произвести такое число опытов (измерений), при котором

P{ my − MY < ε} < β

Интервал (MY −ε, MY +ε) называется доверительным интервалом.

Для определения интервальных оценок можно воспользоваться следующим алгоритмом:

1)определить оценки математического ожидания my и дисперсии s2y ;

2)определить дисперсию оценки математического ожидания:

3) определить доверительный интервал для оценки математического ожидания при доверительной вероятности β=0,95: