Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Дальневосточный федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

6 Филатова Моделирование биотехнических систем.pdf

Скачиваний:

201

Добавлен:

01.05.2015

Размер:

2.3 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1413 14 > Следующая >>>

118

5. ПРИМЕНЕНИЕ СИСТЕМЫ MATLAB

ДЛЯ РЕШЕНИЯ ЗАДАЧ МОДЕЛИРОВАНИЯ ЭЛЕМЕНТОВ БТС

5.1. Общая характеристика системы MATLAB

Система MATLAB является одной из самых мощных в компьютерной математике. Разработчиком базового ядра системы, а также его многочисленных расширений является корпорация MathWorks Inc (USA). (http // www.mathworks.com).

Это одна из старейших систем математических расчетов, построенных на реализации матричных операций. Одним из главных достоинств системы является ее открытость и расширяемость. Эти свойства проистекают из наличия специального (очень простого) языка программирования высокого уровня. Большинство команд и функций системы реализованы в виде m- файлов (текстовые файлы) и файлов на языке Си. Все файлы доступны для модификации.

Ядро системы включает программу-интерпретатор команд, что позволяет проводить вычисления и отладку в удобном пошаговом режиме. В качестве средства повышения производительности следует упомянуть специальный компилятор.

Система MATLAB является лидером в области реализации численных методов и методов математического моделирования.

Систему сопровождает большое количество М-файлов (расширение *.m), содержащих демонстрационные примеры и определения новых операторов и функций. Эта библиотека, все файлы которой снабжены обширными комментариями, позволяет изучать исходный текст модулейфункций. Система имеет открытую архитектуру, что позволяет изменять существующие функции и добавлять свои, новые.

Система MATLAB интегрирует около 50 программных продуктов. В ядро системы входят базовая версия MATLAB и пакет моделирования Simulink. Все расширения системы объединены в модуль Toolbox.

Система поддерживает несколько режимов работы, основными являются командный (режим прямых вычислений) и программно-исполняемый (режим исполнения программ, в котором осуществляется интерпретация или запуск компилированных бинарных файлов).

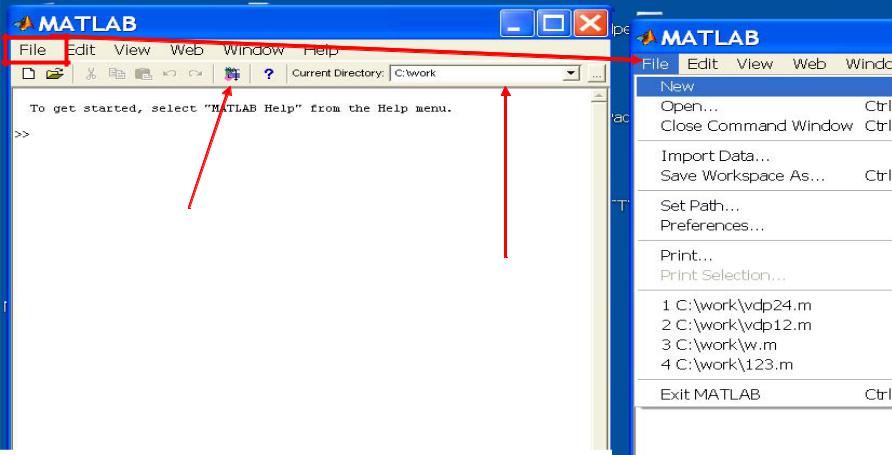
При запуске системы MATLAB на экран выводится командное окно (рис.5.1), которое используется для ввода отдельных команд и выполнения вычислений в режиме интерпретации. Управляющее меню включает группы команд работы с файлами (File), редактирования, настройки окон интерфейса, вывод панелей инструментов (View) (рис.5.2), поддержку работы системы через Internet (Web) и др.

Запуск Simulink

Рабочая папка

Рис.5.1. Командное окно при запуске системы MATLAB

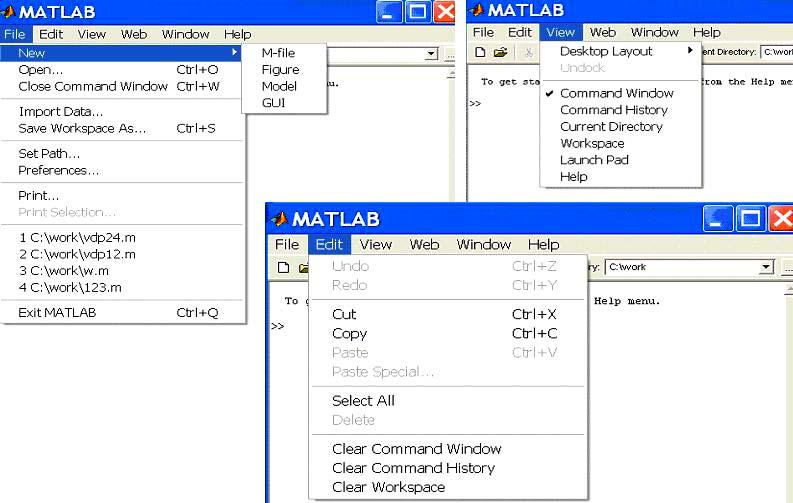
Рис.5.2. Команды работы с файлами (File), редактирования (Edit), настройки окон интерфейса (View)

121

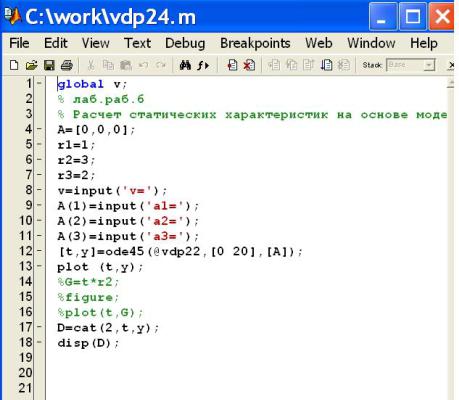
Команда File / New / M-file открывает окно редактора и отладчика М-файлов (рис.5.3). Это текстовые файлы, написанные на входном языке высокого уровня.

Рис.5.3. Окно редактора и отладчика М-файлов

Кроме основных для всех проблемно-ориентированных языков команд входной язык поддерживает обращение к множеству специальных функций и модулей, позволяющих решать задачи фильтрации, спектрального, дисперсионного, кластерного анализа и т.д. После ввода текста программы и ее сохранения в М-файле программа может ставиться на выполнение

(команда Debug // Run ).

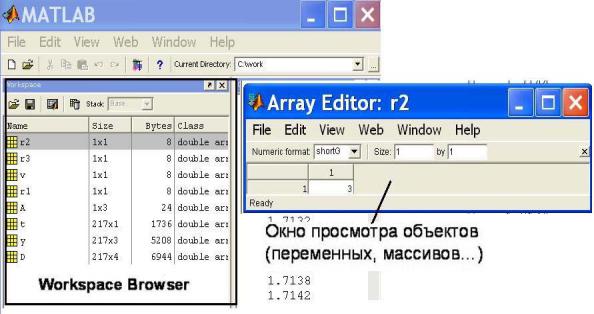
Система ориентирована прежде всего на реализацию матричных вычислений, т.е. на обработку больших массивов и векторов. Для просмотра результатов вычислений имеется специальное окно Workspace Browser – просмотр ресурсов рабочего пространства памяти (рис.5.4).

Текстовые М-файлы можно создавать в специальном редакторе, который выполняет функции: редактирование текста программы, синтаксический контроль, расстановка контрольных точек в теле программы (для приостановки вычисления и промежуточной оценки результатов), сохранение программы в текстовом файле. Для набора программы можно использовать также любой текстовый редактор, поддерживающий формат

ASCII.

122

Рис.5.4. Окно Workspace Browser – просмотр ресурсов рабочего пространства памяти

При выполнении синтаксического контроля введена цветовая разметка: ключевые слова – синий цвет; операторы, константы и переменные – черный;

комментарии после знака % - зеленый цвет; символьные переменные (в апострофах) – коричневый цвет; синтаксические ошибки – красный цвет.

М-файлы, создаваемые отладчиком, делятся на файлы функции, имеющие входные параметры (рис.5.5) и - файлы-сценарии, не имеющие входных параметров.

Файл-функция имеет входные параметры, входящие в него переменные являются локальными.

Файл-сценарий не получает данных извне с помощью списка входных параметров, это простая процедура без параметров. Может использовать глобальные переменные, является просто записью серии команд без входных и выходных параметров (рис.5.6).

Файл-сценарий имеет следующую структуру:

%Основной комментарий %Дополнительный комментарий

Тело файла с любыми выражениями.

Для файлов-сценариев характерно отсутствие входных и выходных аргументов, работа с данными из рабочей области. В процессе выполнения они не компилируются и могут рассматриваться как аналог сессии.

123

Рис.5.5. Пример файла функции

Рис.5.6. Пример файла сценария

Файл-функция является объектом языка программирования системы MATLAB. С точки зрения структурного программирования он является полноценным модулем. Структура файла-функции приведена в табл.5.1.

Функции могут быть встроенные (внутренние) и внешние (М-

124

функции). Встроенные функции хранятся в откомпилированном ядре системы MATLAB, поэтому они выполняются очень быстро. Внешние функции содержат свои определения в М-файлах. Задание таких функций возможно организовать при написании новых М-файлов.

	Таблица 5.1.
Команды	Коментарии
Function	Объявление типа
var=f_name(список параметров)	Объявление типа
Function	Имя переменной выходного пара-
var	метра
f_name	Имя функции
(список параметров)	Список входных паарметров

При обнаружении файла-функции он компилируется и затем исполняется, а созданные машинные коды хранятся в рабочей области системы

Var=выражение	Вводится, если требуется, чтобы
	функция возвращала результат вы-
	числения.

Простейшие формы команды вывода графиков показаны в табл. 5.2. Таблица 5.2.

Задача Команда Результат выполнения команды

Построить график функ-				>> x=0:0.1:10;
ции	sin(x)	на интервале		>> plot(sin(x))		Рис. 5.7
от 0	до 10, с шагом 0,1					(No 1)
Построить графики				> x=0.1:0.1:10;
функций		y1(x);	y2(x);	>> y1=sin(x); y2=cos(x);		Рис. 5.8
y3(x) на интервале от 0.1				y3=sin(x)./x;	(деление	Рис. 5.8
до 10, с шагом 0,1				вектора на массив)		(No 1)
				>> plot(x,y1,x,y2,x,y3)
				вывод трех графиков
Построить графики				> x=0.1:0.1:5;
функций y1(x); y2(x); в				>> y1=sin(x); y2=cos(x);		Рис. 5.9
окне 1,				y3=sin(x)./x;	(деление	Рис. 5.9
y3(x) в окне 2				вектора на массив)		(No 1 и
на интервале от 0.1			до 5,	>>plot(x,y1,x,y2) вывод		No 2)
с шагом 0,1				двух графиков в окне 1
				>> figure;
				>> plot(x,y3) вывод 3-го
				графика в окне 2

125

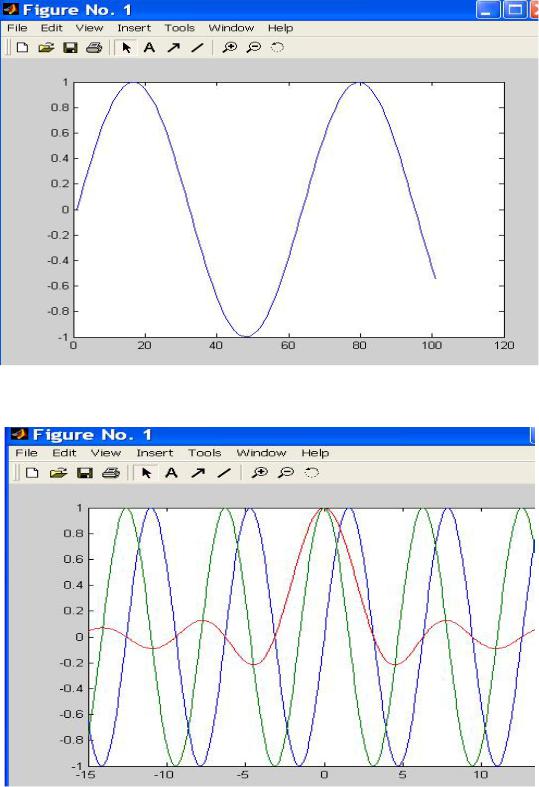
Рис.5.7. Пример формирования графика функции sin(x)в отдельном окне

Рис.5.8. Пример формирования графиков функций sin(x); cos(x); sin(x)./x в одном окне

Для построения М-файлов используются простейшие управляющие структуры (табл.5.3).

126

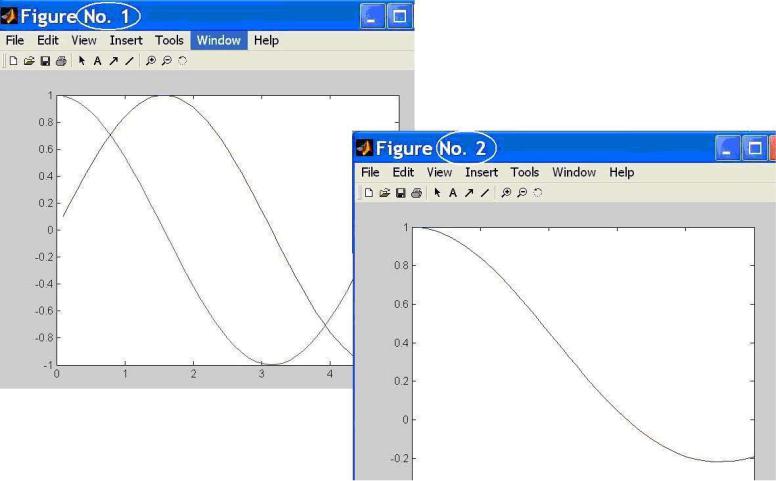
Рис.5.9. Вывод графиков в двух окнах

		127
			Таблица 5.3.

Команды (операторы)			Комментарии

r=input(‘ввод радиуса = ‘);			диалоговый ввод данных
			Допустим ввод символьных вы-
			ражений

Disp(‘длина	окружности=	‘);	вывод результата
disp(2pir)

If Условие			Условный оператор
Инструкции
End

If Условие			Условный оператор
Инструкции 1
elseIf Условие
	Инструкции 2
else
End	Инструкции 3
End

If Условие			Условный оператор
Инструкции 1			Инструкции в списке разделяются
else	Инструкции 2		запятой или точкой с запятой
End

For var=выражение,			Циклы типа for-end
Инструкция,…Инструкция			Выражение :: s:d:e
End			s –начальное значение пере-
			менной цикла,
			d- шаг (если не указан, то d=1),
			e – конечное значение переменной
			цикла
			Пример.
			For x=0:0.25:1 x^2, end

While Условие			Циклы типа While
Инструкции
End

128

5.2. Численный анализ моделей элементов биотехнических систем

Для реализации численных методов решения систем дифференциальных уравнений имеется библиотека различных методов, так называемых решателей (solver) [20]. В табл. 5.4 приведены основные решатели и их характеристики, области их применения описаны в табл. 5.5.

					Таблица 5.4
N	Решатель		Характеристики

1	ode45		Одношаговые явные методы Рунге-Кутта 4-го и 5-
			го порядка. Это классические методы, рекоменду-
			ются для начальной пробы решения.
			Во многих случаях дают приемлемые (хорошие)
			результаты
2	ode23		Одношаговые явные методы Рунге-Кутта 2-го и 4-
			го порядка. При умеренных требованиях к жестко-
			сти СОДУ и точности решения этот метод может
			дать выигрыш в скорости решения.
3	ode113		Многошаговый метод Адамса-Мултона переменно-
			го порядка. Адаптивный метод, который может
			дать высокую точность решения.
4	ode23tb		Неявный метод Рунге-Кутта в начале решения и
			метод, использующий формулы обратного диффе-
			ренцирования 2-го порядка в последующем.
					Таблица 5.5
Решатели		Тип задачи		Степень	Область применения
				Точности

ode45		Нежесткая		Средняя	В большинстве случаев
ode23		Нежесткая		Низкая	При допустимости грубой по-
					грешности или при решении
					умеренно жестких задач
ode113		Нежесткая		От низкой	При высокой точности реше-
				до высокой	ния или при решении сложных
					в вычислительном отношении
					задач
ode23tb		Жесткая		Низкая	При уравнениях, заданных в
					неявной форме Коши.

129

Рассмотрим подготовку исходных данных для численного анализа уравнений смесительной модели (3.26), (3.27):

dV	= G1 +G2 −G3				и		V (t) = S H (t);			(5.1)
dt	= G1 +G2 −G3				и		V (t) = S H (t);
dt		d(VCA2 )
		d(VCA2 )	= G C			A1	−G C		;
			= G C				−G C		;
		dt		1			3	A2
		dt
		d(VCB2 )	= G C			B1	−G C		.
			= G C				−G C		.
		dt		2			3	B2
		dt

Для обращения к одному из решателей из табл.5.5 необходимо преобразовать уравнения модели в форму Коши:

dY	= F(Y ,t).	(5.2)
dt	= F(Y ,t).
dt

Если V=const, то (5.1) преобразуется к виду

или

G3 = G1

+G2;

(5.3)

dCA2

(G C

−G C

);

dCB2

(G C

−G C

Исходными данными для решения системы (5.3) являются начальные условия Y(t=0) и интервал решения t0 < t ≤ tfinal .

Обращение к решателю имеет вид

[T,Y]=solver(‘F’,[t0 tfinal],y0).	(5.4)
С учетом (5.2) и (5.3) вектор имеет две составляющие:	(5.5)
Y = ( y1, y2 ) и y1 = CA2 , y2 = CB2.	(5.5)

В этой функции (5.4) кроме начальных условий и интервала для изменения независимого аргумента указывается имя (‘F’) так называемого ODE-файла, в котором описывается правая часть исходной системы дифференциальных уравнений.

С учетом (5.5) ODE-файл с описанием правой части системы (5.3) имеет вид

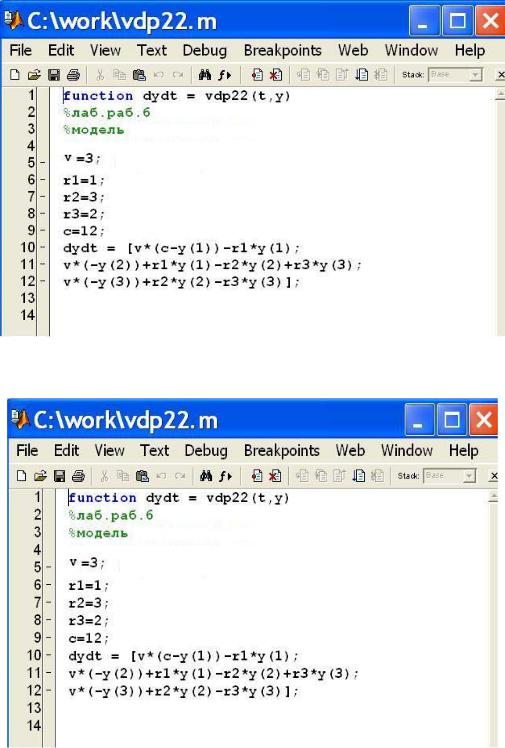
function dydt = vdp25(t,y)

%смесительная модель при постоянном объеме

%исходные данные

G1=1;

G2=3;

130

CA1=15;

CB1=10;

W=1/V;

G3= G1+ G2;

% правая часть системы дифференциальных уравнений в форме Коши

dydt = [W*(G1*CA1-G3*y(1)); W*(G2*CB1-G3*y(2))];

Сохраняем функцию vdp25(t,y) в файле vdp25.m. Используя командное окно, получаем решение (табл.5.6).

	Таблица 5.6.
Команды	Результат

>> [t,y]=ode45(@vdp25,[0 4],[5 5]);	На экран выводятся графики-
>> plot(t,y);	решения (рис.5.10).
>>hold on;	Дополнение графиков метками (в
gtext('y1'),gtext('y2'),gtext('y3')	ручном режиме)

Рис.5.10. Изменение концентраций в смесительной модели при постоянном объеме(5.3)

131

Для численного анализа полной смесительной модели (5.1) введем обозначения

y1(ti ) = S H (ti ) CA2 (ti );

(5.6)

y2 (ti ) = S H (ti ) CВ2 (ti );

y3 (ti ) = S H (ti ).

Тогда система (5.1) примет вид

dy1

= G +G −G ;

(5.7)

d( y2 )

= G C

−G C

;

d( y3 )

= G C

−G C

;

CA2

(ti ) =

y2 (ti )

CB2

(ti ) =

y3 (ti )

y (t

)

С учетом (5.7) вектор Y имеет три составляющие:

Y = ( y1, y2, y3 )

и y1 =V ,

y2 = (CA2 y1 ), y3 = (CB 2 y1 )

(5.8)

Тогда ODE-файл с описанием правой части системы (5.7),(5.8) имеет

вид

function dydt = vdp26(t,y)

G1=1.5;

G2=2;

G3=3.5;

%Значения концентрации при статическом равновесии CA1=20 и

CB1=15

%Имитация возмущений по концентрации входных потоков

CA1=40 и CB1=45

CA1=20;

CB1=15;

%правая часть системы дифференциальных уравнений в форме Коши

dydt = [(G1+G2-G3); (G1*CA1-G3*(y(2)/y(1)));

(G2*CB1-G3*(y(3)/y(1)))];

Сохраняем функцию vdp26(t,y) в файле vdp26.m. С помощью этой

132

функции мы получаем массив значений только одной искомой координаты смесительной модели V(t), для определения концентраций смешиваемых веществ необходим пересчет массивов y(i,2) и y(i,3) по соотношениям, получаемым из (5.8):

CA2 (ti ) =	y2 (ti )	,	CB2 (ti ) =	y3 (ti )	.	(5.9)
	y1(ti )
				y1(ti )

Эти команды, как и обращение к решателю, оформим в виде файласценария vdp28.m.

%Смеситель

%Расчет концентраций

%задание начальных условий y1, y2, y3

A=[3,25.71429,25.71429];

%обращение к решателю, интервал времени от 0 до 5, нач.усл=А

[t,y]=ode45(@vdp26,[0 5],[A]);

%Определение числа шагов по оси времени

K=size(t);

N=K(1,1);

% Расчет массива концентраций по (5.9)

for i=1:N CA2(i,1)=y(i,2)/y(i,1), CB2(i,1)=y(i,3)/y(i,1),end;

% Вывод графиков y(t) и CA2(t) CB2(t) plot (t,y);

figure;

plot(t,CA2,t,CB2);

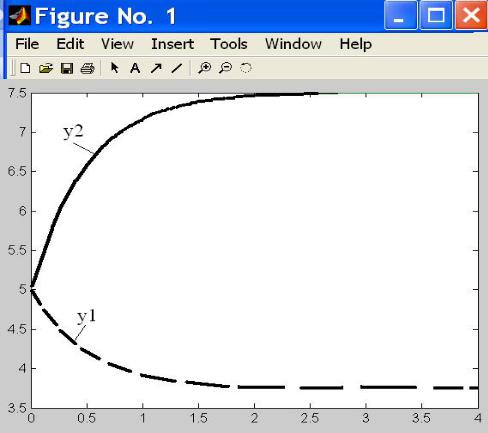
В результате выполнения файла vdp28.m получаем графики (рис.5.11, 5.12).

Рассмотренные примеры реализации смесительной модели позволяют построить программу численного анализа модели процесса газообмена в дыхательной системе.

Программная реализация решения системы (3.29) – (3.30) уравнений материального баланса по углекислоте для легочного и тканевого резервуаров аналогична смесительной модели с постоянным объемом. Обозначим y(1) = Са, концентрации углекислоты в альвеолярном резервуаре, y(2) = Сt, концентрации углекислоты в тканевом резервуаре.

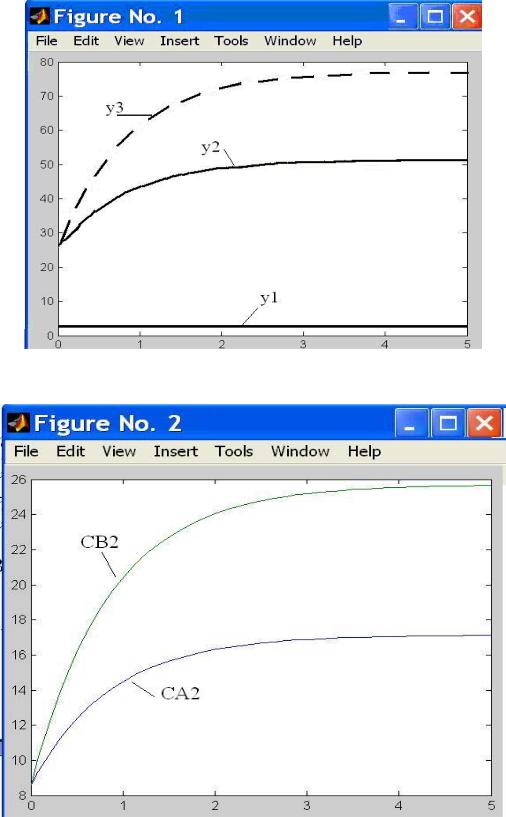
133

Рис.5.11. Изменение составляющих вектора Y в модели (5.7) при возмущениях по концентрациям во входных потоках

Рис.5.12. Изменение концентраций в смесительной модели при возмущениях по концентрациям во входных потоках

134

Тогда ODE-файл с описанием правой части системы (3.30) примет вид function dydt = vdp2(t,y)

%Задаются значения исходных данных

%G1 (воздушный поток на вдохе и выдохе)

%Q1, Q2 потоки венозной и артериальной крови,

%W скорость образования углекислоты в процессе обмена

%С1 - концентрация углекислоты во вдыхаемом воздухе,

%Va, Vt – соответственно объемы альвеолярного и тканевого ре-

зервуаров

%b0 ,b1 - коэффициенты линеаризующей функции F(CA ) = b0 + b1CA .

………………………………………………..

% правая часть системы модели дыхания

dydt = [(G1*C1+ Q1*y(2)-Q2*(b0+b1*y(1))-G1*y(1))/V; (W+Q2*(b0+b1*y(1))-Q1*y(2))/V];

На основе обращений к решателям (табл.5.4) можно построить программы анализа динамических моделей объектов с сосредоточенными координатами.

При рассмотрении моделей, заданных передаточными функциями, удобнее использовать возможности пакета расширения Simulink [20].

Контрольные вопросы

10.Назначение программной системы MATLAB.

11.Основные режимы работы системы

12.Какие средства системы можно использовать для просмотра результатов вычислений?

13.Для чего предназначено окно Workspace Browser ? 14.Чем файлы-функции отличаются от файлов-сценариев ?

15.Какие редакторы можно использовать для создания М-файлов ? 16.Для чего используются решатели (solver`s) ?

17.Приведите примеры решателей, которые включены в библиотеку

MATLAB.

135

18.Какие исходные данные необходимы для численного анализа уравнений упрощенной математической модели процесса газообмена в дыхательной системе:

d(VАCA )

= G C +Q C −Q F(C ) −G C ;

(5.10)

1 1

1 t

d(Vt Ct )

=W +Q F(C

) −Q C

;

1 t

VA ,Vt

= const.

При

19.Составьте ODE-файл с описанием правой части системы (5.10).

20.Какие исходные данные необходимы для численного анализа уравнений компартментной системы движения йода в организме млекопитающего

dV1

= r

+ r

− r

−V

− S H

+ z);

(5.11)

dV2

(u H 2 − S H

+ z) + r

− r

−V

Q ;

dV3

− r

−V

(AH

+ r );

r31H3

H1r17

dH1

r21H2

−

− H V

(u H 2 − S H

+ z);

dH2

= H V (u H

2 − S

+ z) +

r32 H3

−

H2 r21

− H

;

dH3

= H

−

+ r ) − S

(AH

+ r ),

при V5

= const и H4

= const.

21.Составьте ODE-файл с описанием правой части системы (5.11).

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1413 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.2015150.84 Кб104.02.docx
#
01.05.201538.7 Кб184.04. Дальний Восток в первой половине ХХ века.pdf
#
02.08.2019290.82 Кб54k_pulmunologia_kardiologia_test.doc
#
01.05.2015443.9 Кб564_Глава 2.doc
#
01.05.20151.93 Mб3445. Метрология, стандартизация и сертификация.pdf
#
01.05.20152.3 Mб2016 Филатова Моделирование биотехнических систем.pdf
#
01.05.2015407.75 Кб106.pdf
#
20.08.201983.97 Кб36_peredelala.doc
#
01.05.20151.23 Mб427 и 8 рацион. выбор пол. сети.rtf
#
01.05.2015140.5 Кб875662209.pdf
#
10.03.2016284.16 Кб127_instrumentov_UK.doc