
- •ВВЕДЕНИЕ
- •1.1. Понятие моделирования
- •1.2. Виды моделирования
- •1.2.1. Физическое моделирование
- •1.2.2. Математическое моделирование
- •1.3. Классификация математических моделей
- •1.4. Понятие об адекватности математической модели
- •МОДЕЛИРОВАНИЯ
- •Рис.2.1. Блок-схема объекта моделирования
- •2.2. Пассивный эксперимент: общая характеристика
- •2.3. Понятие об уравнении регрессии
- •2.4. Построение линейной модели статики
- •Таблица 2.2
- •Рис.2.4. Блок-схема объекта (при n=1)
- •2.5. Регрессионный анализ результатов моделирования
- •Рис.2.6. Тональная аудиограмма при остром среднем отите
- •2.5.3. Проверка гипотезы об адекватности математической модели
- •2.6. Построение множественной линейной модели
- •2.8. Математические модели на основе активных экспериментов
- •3.2. Модели, характеризующие режим течения материального потока
- •4. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ БТС
- •4.1. Понятие об имитационном моделировании
- •4.2. Понятие о компартментной системе
- •5. ПРИМЕНЕНИЕ СИСТЕМЫ MATLAB
- •ДЛЯ РЕШЕНИЯ ЗАДАЧ МОДЕЛИРОВАНИЯ ЭЛЕМЕНТОВ БТС
- •ЗАКЛЮЧЕНИЕ
75
Интерпретация вектора входных (Х) и вектора выходных (Y) координат элемента БТС в разных задачах может быть различной. При исследовании электрических импульсов, электрических элементов БТС применяют законы Кирхгоффа. При изучении процессов газообмена – уравнения материального баланса по отдельным компонентам и т.д.
Модели отличаются смысловыми коэффициентами, интерпретацией отдельных составляющих и допущений.
Несмотря на существенные различия в структуре отдельных органов, а также в отдельных физиологических процессах при разработке моделей на основе уравнений сохранения вещества и энергии можно использовать типовые идеализированные решения. Это так называемые типовые модели, описывающие структуры материальных потоков. Подобный подход позволяет упорядочить методическую сторону задачи моделирования.
3.2. Модели, характеризующие режим течения материального потока
Математическая модель, описывающая движение материальных потоков в некоторых элементах биотехнической системы, позволяет изучать изменения запасов определенного вещества (например, запасов йода в организме или лекарства, наркотика в крови) в объеме отдельного органа или всего объекта в целом. Подобные модели могут использоваться и для описания движения материальных потоков в фармакологических и иных производствах.
Для описания движения материальных потоков введем предварительные понятия о типах моделей объектов, в которых наблюдаются эти материальные потоки. Будем различать модели объектов: двухполюсные, смесительные, разделительные и сложные [8].
Двухполюсные модели имитируют работу на проток, смесительные модели отображают объект, к которому подходит несколько потоков, а выходит только один поток. Разделительные модели отображают случай, противоположный смесительной модели, а сложные модели – комбинацию всех предыдущих моделей.
Среди двухполюсных моделей принято различать модели: источников (истоки), сопротивления, емкостные модели, индуктивные, реакторные.
Модели источников – это модели элементов, создающих потенциальную или кинетическую энергию (примеры, компрессоры, насосы, нагреватели, запас основных клеток в костном мозгу).
Резистивные модели (компоненты) – это модели элементов, рассеивающих энергию системы (примеры, гидравлические сопротивления, клапаны, участки трубопроводов, участки кровеносных сосудов).
76
Емкостные модели (компоненты) – это модели элементов, обладающих способностью накапливать вещество или энергию системы, а также отражающих свойства упругости веществ.
Индуктивные модели (компоненты) – это модели элементов, характеризующих инерционный эффект массы в потоке вещества.
Реакторные модели – это модели с одним входным потоком.
Всем реальным объектам, не зависимо от того, каким типом модели он описывается, присущи два общих признака:
-в любом реальном объекте при движении материального потока (протекании потока через объект) происходит аккумулирование части поступившего материала, т.е. часть потока теряется (накапливается) в объеме объекта;
-ко всем объектам, в которых происходит движение материальных потоков, применим закон сохранения масс. Масса вошедшего в объект материала за временной интервал Т равна массе вышедшего за этот период времени материала с учетом аккумулированного вещества.
Сучетом этих свойств в моделях необходимо отражать отличие характеристик выходных потоков от характеристик входных потоков, причем эти отличия должны быть связаны как с характером движения, так и с прочими (не гидравлическими) процессами (химическими, термическими, механическими).
Основное внимание при разработке емкостных моделей уделяют описанию структуры потока внутри моделируемого объекта. При этом т.к. уравнения гидродинамики реальных потоков имеют очень сложный вид (решаются только численно), то используют специальные идеализированные модели. Если объект включает больше одного потока, модели составляются для каждого потока в отдельности.
Рассмотрим первый вид такой модели: модель идеального смешения. Ее основными допущениями являются следующие утверждения:
-любое изменение концентрации на входе в зону идеального смешения
Свх мгновенно распространяется по всему объему V и поступающий в
модель поток мгновенно перемешивается с находящимся там материалом; - содержание компонента потока во всех точках рабочего объема зоны идеального смешения (С) и на выходе из нее в каждый момент времени
одинаково C(ti ) = Cвых(ti ) ;
-объемная скорость потока не изменяется, ϑ = const ;
-C = f (t) – непрерывная функция времени.
Сучетом введенных допущений справедливы предположения, что
∂C |
= 0, |
∂C |
= 0, |
∂C |
= 0; ϑ |
=ϑ ; V = const; H = const. |
|
∂Z |
∂R |
∂(−Z ) |
|||||
|
|
вх |
вых |
||||
|
|
|
|
|

77
Количество меченого вещества во входном и выходном потоках будет:
Iвх =ϑ Cвх; Iвых =ϑ Cвых. (3.1)
В условиях статического равновесия на основе закона сохранения массы эти величины равны:
Iвх = Iвых .
Если статическое равновесие нарушено Iвх ≠ Iвых , то в зоне идеального
смешения накапливается (аккумулируется) некоторое количество вещества
M :
t |
(3.2) |
M = ∫(Iвх − Iвых )dt.
0
Если разделить правую и левую части уравнения (3.2) на объем зоны V, то в левой части уравнения получим приращение концентрации меченного вещества, которое произошло за рассматриваемый интервал времени:
|
|
M |
C =C(t) −C(0). |
(3.3) |
|||||
|
|
|
= |
|
|||||
|
V |
|
|||||||
Подставим (3.1) в (3.2), с учетом (3.3) получим |
(3.4) |
||||||||
C(t) −C(0) = |
t |
1 |
(ϑ Cвх −ϑCвых )dt. |
||||||
|
|
|
|||||||
|
|
|
|
||||||
|
|
|
|
|
∫V |
|
|||
|
|
|
|
|
0 |
|
|
|
|
Продифференцируем (3.4) по времени, получим |
(3.5) |
||||||||
|
|
dC |
= |
ϑ (Cвх −Свых ). |
|||||
|
|
|
|
||||||
|
|
dt |
V |
|
|
|
|||
Уравнение (3.5) описывает процесс идеального смешения и используется для построения стационарных моделей с сосредоточенными координатами. Основным параметром модели является время пребывания частиц меченного вещества в пределах зоны смешения
τ = Vϑ .
Решение уравнения идеального смешения во временной области задается уравнением вида
C = Cvx (1 − l− |
t |
(3.6) |
|
τ |
), |
|
|
которому можно поставить в соответствие передаточную функцию инерционного звена первого порядка:
W = τp1+1.
Условия, приближенные к идеальному смешению, обычно можно воспроизвести в замкнутом объеме, в зоне, высота которой примерно равна ее
78
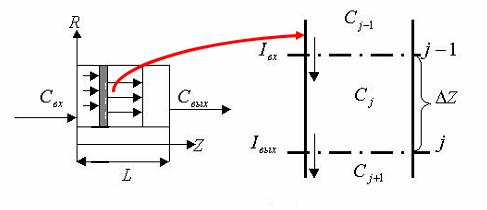
диаметру. В тех случаях, когда для объекта моделирования характерно наличие протяженных участков, прототипом становится уравнение идеального вытеснения. Допущения модели идеального вытеснения включают следующие утверждения:
-линейная скорость потока не изменяется, U =const;
-концентрация меченного вещества в потоке изменяется не только во
времени, но и по длине потока C = f (t, z) ;
-в направлении, перпендикулярном движению, субстанция распределена равномерно, т.е. в пределах любого сечения материального потока выполняются допущения об идеальном смешении (рис.3.1);
-время пребывания в системе всех частиц одинаково.
Сучетом введенных допущений справедливы предположения, что
∂C |
≠ 0; |
∂C |
= 0; |
∂C |
= 0. |
|
∂Z |
∂R |
∂(−Z ) |
||||
|
|
|
(а) |
|
|
|
(б) |
|
|
|
|
Рис.3.1. Условные обозначения ячейки идеального смешения (а) и одного выделенного сечения ячейки (б)
Для вывода уравнения идеального вытеснения рассмотрим произвольное сечение толщиной Z, в пределах которого выполняются допущения об идеальном смешении, и концентрация меченного вещества равна Сj . Аналогичным образом выделяются предыдущая ячейка с концентрацией Сj−1 и последующая с концентрацией Сj +1 .
Для выделенной j-й ячейки количество меченного вещества во входном и выходном потоках соответственно равно:
Iвх = I j−1; Iвых = I j ; I j−1 =U S C j−1; I j =U S C j , |
(3.7) |
где U – линейная скорость потока, S – площадь сечения, Сj −1 – кон-
центрация меченного вещества в соответствующей ячейке.
Если статическое равновесие нарушается, то в пределах выделенной ячейки накапливается некоторое количество меченного вещества:
79
С учетом (3.7) получим |
Iвх ≠ Iвых → M. |
(3.8) |
|
(3.9) |
|
t |
t |
|
M = ∫(Iвх − Iвых )dt = ∫U S(C j−1 −C j )dt. |
||
0 |
0 |
|
Разделим обе части уравнения на объем ячейки ( |
V), тогда в левой час- |
|
ти уравнения (3.9) получим изменение концентрации меченного вещества, которое произошло за интервал времени t:
M |
= C(t) −C(0). |
(3.10) |
V |
|
|
В правой части уравнения (3.9) вынесем за скобку знак минус и постоянные параметры, уравнение примет вид
C(t) −C(0) = |
U S |
∫t |
−(C j −C j−1 )dt |
|||
V |
||||||
. |
0 |
|
|
|
||
|
|
|
|
|
|
|
Обозначим |
V = Z S, |
1 = C j −C j−1 . |
||||
|
||||||
Тогда уравнение (3.12) примет вид |
|
|
||||
|
C(t) −C(0) = −U ∫t |
1 |
dt. |
|||
|
Z |
|||||
|
|
|
|
0 |
|
|
(3.11)
(3.12)
(3.13)
Продифференцируем по времени левую и правую части уравнения
(3.13) и перейдём к пределу при |
Z →0 : |
(3.14) |
|||
∂C = −U lim |
|
1 |
. |
||
|
|
||||
|
|
|
|||
∂t |
Z→0 |
Z |
|
||
Получим уравнение вида |
|
|
|
|
(3.15) |
∂C = −U ∂C . |
|||||
|
|
|
|
|
|
∂t |
∂Z |
|
|
|
|
Уравнение (3.15) – это уравнение идеального вытеснения, которое используется при моделировании объектов с распределенными координатами, стационарными.
Рассмотрим пример другой формы записи уравнения модели идеального вытеснения. Для этого перенесем все члены уравнения (3.15) в левую часть:
∂C |
+ U |
∂C |
=0 |
(3.16) |
∂t |
|
∂Z |
|
|

80
и перейдем в область изображений по Лапласу, при этом введем следующее обозначение для решения уравнения C(Z,t) = f (Z,t) и его изобра-
жения Ф(Z, p) . Тогда изображение уравнения (3.16) примет вид
U |
dФ(Z, p) |
+ pФ(Z, p) = 0. |
(3.17) |
dZ |
|
||
|
|
|
Решение обыкновенного дифференциального уравнения первого порядка можно найти аналитическим путем:
|
p |
(3.18) |
|
Ф(Z, p) = λe− |
|
Z . |
|
U |
|
||
Здесь для определения коэффициента λ необходимо задать начальные условия. Так как в (3.18) один независимый аргумент – длина (Z), то начальные условия должны определять искомую функцию на входе в ячейку, т.е. Ф(Z, p) при Z=0. Тогда
|
p |
(3.19) |
|
Ф(0, p) = λe−( |
|
)*(Z =0) |
= λe0 = λ*1 = λ. |
U |
|||
Если ввести параметр τ = UZ , характеризующий время пребывания
частиц меченного вещества в зоне идеального вытеснения, то уравнение (3.19) привет вид
|
Z |
(3.20) |
|
Ф(Z, p) = λe− |
|
p |
= λe−τp . |
U |
|||
Уравнение (3.20) определяет изображение концентрации меченного вещества в любой точке по длине зоны идеального вытеснения, в том числе и на выходе (Z=L).
Учитывая, что отношение изображения выхода к изображению входа определяется как передаточная функция объекта моделирования, получим
W = |
Ф(L, p) |
|
λe |
−τp |
(3.21) |
= |
|
= e−τp . |
|||
|
Ф(0, p) |
|
λ |
|
|
Модели идеального смешения и идеального вытеснения представляют собой примеры чрезвычайно упрощенных способов описания физических процессов. Это своеобразные точки репера, к которым в отдельных случаях удается приблизиться. Для описания реальных процессов, связанных с перемещением жидких или газообразных потоков, используют более точные, но и более сложные уравнения диффузионных моделей.
Однопараметрическая диффузионная модель основана на допущениях общих с моделью идеального вытеснения, отличие состоит в том, что новая модель предусматривает существование обратного перемешивания:
∂C ≠ 0; |
∂C = 0; |
81 |
|
|
|
|
∂C ≠ 0. |
(3.22) |
|||
|
|
|
|
|
|
∂Z |
∂R |
|
|
|
|
|
∂(−Z ) |
|
|
||
Уравнение однопараметрической диффузионной модели используют при описании объектов с распределенными координатами:
∂C |
= −U |
∂C |
+ D |
2 |
C |
(3.23) |
∂ |
, |
|||||
∂t |
|
∂Z |
|
L ∂Z 2 |
|
|
где DL – коэффициент, определяемый экспериментально, учитывает турбулентную диффузию или перемешивание.
Двухпараметрическая диффузионная модель еще больше ослабляет допущения и предусматривает существование перемешивания в радиальном направлении:
∂C |
≠ 0; |
∂C |
≠ 0; |
∂C |
≠ 0. |
|
∂Z |
∂R |
∂(−Z ) |
||||
|
|
|
Уравнение двухпараметрической диффузионной модели имеет вид
∂C |
= −U |
∂C |
+ D |
∂2C |
+ |
D |
R |
|
∂ |
(R |
∂C |
), |
(3.24) |
∂t |
∂Z |
L ∂Z 2 |
R ∂R |
∂R |
|
||||||||
|
|
|
|
|
|
||||||||
где DR – коэффициент радиального перемешивания, определяемый экспериментально, учитывает турбулентную диффузию или перемешивание.
Главными недостатками диффузионных моделей является сложность установления граничных условий для уравнений модели и необходимость предварительной оценки коэффициентов обратного и радиального перемешивания.
Взависимости от физической интерпретации составляющих векторов X и Y на основе уравнений типовых моделей структуры потоков можно создавать математические модели, отображающие динамику изменения не только концентрации, но и других характеристик исследуемого объекта.
Втабл. 3.1 приведены уравнения математических моделей для двух различных вариантов векторов X и Y.
Сравнение выполнено для наиболее простых моделей идеального смешения и идеального вытеснения.
Вмоделях, описывающих процессы теплообмена, составляют уравнения для каждого отдельного теплового потока, определяя условия движения и допущения.
Например, описание теплового взаимодействия двух потоков через разделительную стенку на основе допущений об идеальном смешении для обоих потоков.
82
Таблица 3.1
X и Y – концентрации входного и X и Y – температура входного и вывыходного потоков ходного потоков
Уравнения на основе допущений об идеальном смешении
dC |
= |
ϑ (C |
|
−С |
|
) |
V |
ρ |
|
dT1 |
= w ρ |
(T |
−T ), |
dt |
|
|
1 dt |
||||||||||
|
V |
вх |
|
вых |
|
1 |
|
1 1 |
1bx |
1 |
|||
V– объем зоны смешения, ρ – удельная теплоемкость потока, w – расход потока, T1 – температура потока (горячего), отдающего тепло.
Уравнения на основе допущений об идеальном вытеснении
∂C |
= −U |
∂C |
S1 |
ρ1 |
∂T1 |
= −w1 |
ρ1 |
∂T1 |
|
∂t |
∂Z |
∂t |
∂Z |
|
|||||
|
|
|
|
|
|
S – площадь поперечного сечения зоны
В уравнениях введены обозначения: T2 – температура нагреваемого потока (холодная), T1 – температура нагревающего потока (горячего), F – площадь разделительной поверхности между горячим и холодным потоками, K – коэффициент теплопередачи.
V |
ρ |
|
dT1 |
=V ρ |
(T |
−T ) − FK(T |
−T ). |
(3.25) |
|
1 dt |
|
||||||||
1 |
|
1 1 |
1bx |
1 |
1 |
2 |
|
||
На основе уравнений типовых моделей (3.5), (3.15), (3.23), (3.24) можно построить различные виды смесительных и разделительных моделей.
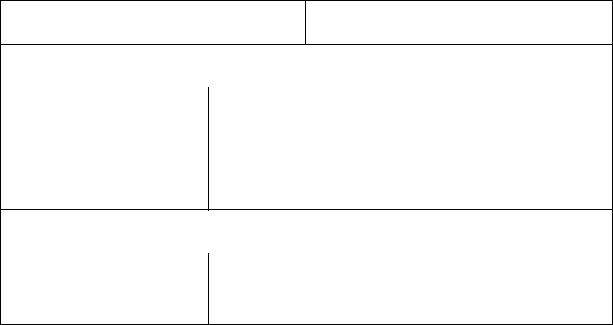
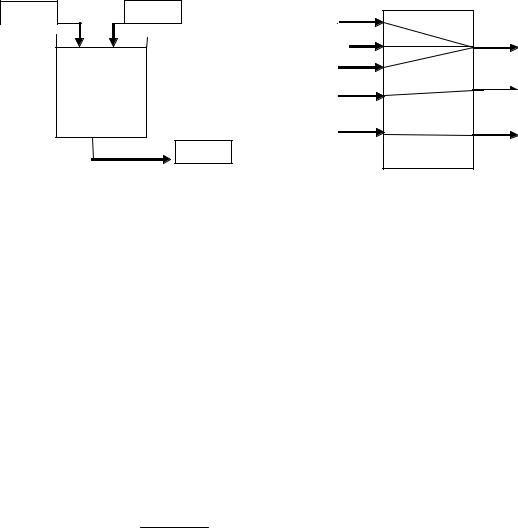
Рассмотрим пример построения модели смесительного типа (рис.3.2а). Объект моделирования условно представлен емкостью, в которую посту-
пает два потока с характеристиками расхода (G1 ,G2 ), состава (CA1 ,CБ1 ). Выходной поток соответственно имеет характеристики G3 ,CA2 ,CБ2
(рис.3.2 б).
Для построения уравнений математической модели используем уравнения вида (3.5). Общий материальный баланс:
dV |
= G |
+G |
−G . |
(3.26) |
dt |
1 |
2 |
3 |
|
|
|
|
|
Для построения уравнения материального баланса по отдельному веществу используем следующую схему.
[скорость накопления вещества ] = = [количество вещества поступающего с потоком входящим] –
– [количество вещества удаляемого с потоком выходящим].
|
|
83 |
|
Поток 1 |
Поток 2 |
G1 |
H |
|
|
|
G2
G3 |
|
СА1 |
СА2 |
СВ1 |
|
Поток 3 |
СВ2 |
|
|
(а) |
(б) |
Рис.3.2. Смесительная модель: а - схема процесса смешения; б – составляющие вектора Х и У модели
Так как в качестве шаблона используется уравнение модели идеального смешения (3.5), приняты допущения о том, что в любой момент времени концентрация каждого вещества в выходном потоке и внутри емкости считаются одинаковыми (CА2 (ti ) = CА(ti ),CB2 (ti ) = CB (ti )) .
Количество вещества в потоке определяем как G C , а скорость накопления вещества в емкости, характеризующую изменение количества веще-
ства в аппарате за интервал времени dt, определяем как |
d(VC) |
. Тогда |
dt |
уравнения материального баланса по веществу А и Б примут вид
d(VCA2 ) = G C |
|
−G C |
|
; |
(3.27) |
|
dt |
1 |
A1 |
3 |
A2 |
|
|
|
|
|
|
|
|
|
d(VCdt B2 ) = G2CB1 −G3CB2 .
Численный анализ уравнений смесительной модели (3.26)-(3.27) можно выполнить с помощью программной системы MatLab. Эти вопросы рассматриваются в главе 5.
На основе типовых моделей (3.5), (3.15), (3.23), (3.24) созданы различные виды математических моделей биологических и биотехнических систем, например: модели дыхательной системы [16], модель газообмена в системе внешнего дыхания человека [17], гидродинамическая модель улитки (внутреннее ухо человека) [18], модель кровотока [19] и другие.
3.3. Модель процессов газообмена в дыхательной системе человека
Модель процессов газообмена в дыхательной системе описывает процессы изменения концентрации кислорода и углекислоты в альвеолярном и выдыхаемом потоках воздуха, в артериальной и венозной крови. Обычно процессы обмена кислородом и углекислотой рассматриваются независимо друг от друга. Во всех моделях эти процессы описываются сходными

84
уравнениями. Поэтому довольно полное представление о газообмене в легких можно получить, рассмотрев предложенную Grodins в 1954 г. модель системы обмена углекислоты между легкими, кровеносной системой
итканями (рис.3.3).
Вмодели приняты следующие допущения:
-легкие представляют собой вентилируемый непрерывным потоком воздуха резервуар;
-объем резервуара постоянный, мертвое пространство равно нулю;
-транспортное запаздывание в системе кровотока пренебрежимо мало, им можно пренебречь;
-артериальная и венозная кровь описываются одной и той же кривой поглощения углекислоты;
-парциальное давление углекислоты в альвеолярном и выдыхаемом воздухе равно напряжению углекислоты в артериальной крови;
-напряжение углекислоты в венозной крови равно напряжению углекислоты в тканях.
dVA dt
↓
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Å q3 |
|
|
|
|
Легочный |
|
|
|
|
|
Тканевый |
|||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
резервуар |
|
|
|
|
|
|
резервуар |
||||
|
|
|
|
|
|
|
→ q2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
↓q1
Рис.3.3. Схема модели газообмена в организме
В соответствии с приведенной схемой (рис.3.3) модель представлена двумя взаимосвязанными емкостями: легочным и тканевым резервуарами. В легочный резервуар поступают два материальных потока:
G1, воздушный поток на вдохе и выдохе; Q1 поток венозной крови.
Из легочного резервуара выходят два материальных потока:
G2, воздушный поток на выдохе;
Q2 поток артериальной крови.
Аналогично для тканевого резервуара можно указать следующие источники изменения содержания углекислоты:
85
-образование углекислоты в процессе обмена со скоростью W [мг/с], определяемой уровнем метаболизма,
-поступления с артериальной кровью (с потоком Q2).
Тканевый резервуар имеет один выходной поток, характеризующий эффект вымывания углекислоты с венозной кровью (с потоком Q1).
Введем обозначения:
Va, Vt –объемы альвеолярного и тканевого резервуаров;
Са, Сt – соответственно концентрации углекислоты в альвеолярном и тканевом резервуарах;
С1 – концентрации углекислоты во вдыхаемом воздухе.
Количество углекислоты, поступающей в легкие с вдыхаемым воздухом и кровью, определяется величиной объемной скорости воздуха и крови, и концентрацией углекислоты в соответствующем потоке. Количество углекислоты, переходящее из легких в венозную кровь, зависит от концентрации углекислого газа в альвеолярном воздухе:
q2 = Q2 F(CA ), |
(3.28) |
где F(CA ) – функция, характеризующая зависимость от концентрации
величины поглощения CО2 единицей потока крови. В общем случае это нелинейная функция, однако допустима ее линеаризация функцией вида
F(CA ) = b0 +b1CA. |
(3.29) |
По аналогии с уравнениями смесительной модели (3.27) составляем уравнение материального баланса по углекислоте для легочного и тканевого резервуаров. Учитывая, что VA,Vt = const , получаем
d(VАCA ) |
= G C |
+Q C |
−Q |
F(C |
) −G C |
; |
(3.30) |
||||
|
|
||||||||||
dt |
1 1 |
1 t |
2 |
|
A |
|
1 A |
|
|
||
d(VtCt ) |
|
|
|
|
|
|
|
|
|
||
|
=W +Q F(C |
|
) −Q C |
. |
|
|
|||||
|
|
|
|
|
|||||||
|
dt |
2 |
A |
|
1 t |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
Полученные уравнения (3.29), (3.30) определяют упрощенную математическую модель процесса газообмена в дыхательной системе. Их численный анализ можно выполнить с помощью программной системы MatLab
[15,20].
3.4.Моделирование органов слуха.
3.4.1.Особенности органов слуха, как объекта моделирования
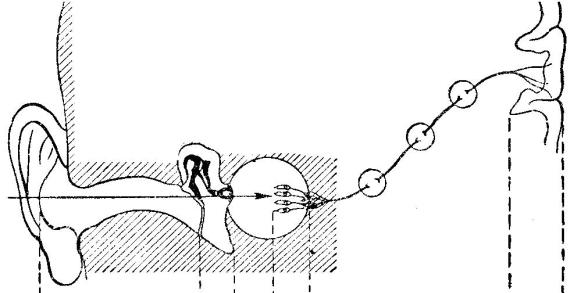
Орган слуха состоит из наружного, среднего и внутреннего уха. Наружное ухо включает ушную раковину и наружный слуховой проход. Слуховой проход заканчивается на своем внутреннем конце тонкой мембраной
86
– барабанной перепонкой, за ней лежит наполненная воздухом полость среднего уха. Эта полость соединена с глоткой узким проходом, так называемой евстахиевой трубой. При глотании происходит некоторый обмен воздухом между глоткой и средним ухом.
В среднем ухе расположены гибко связанные между собой косточки – молоточек, наковальня и стремечко. Один из отростков молоточка слит с барабанной перепонкой. Когда воздушные колебания приводят в движение барабанную перепонку, оно предается костной цепочке. Основание стремечка входит в отверстие в кости, называемое овальным окном. Эта пластинка образует границу между полостью среднего уха и внутренним ухом. Таким образом, цепочка косточек служит мостом между барабанной перепонкой и овальным окном, между атмосферой и внутренним ухом.
Внутреннее ухо находится в височной кости. Из-за своей формы внутреннее ухо называется улиткой. Улитка состоит из трех параллельных, свернутых в катушку трубчатых каналов (вестибулярная лестница). Пластинка стремечка в овальном окне примыкает к вестибулярной лестнице, которая (как и остальные каналы) заполнена жидкостью. Вестибулярная и барабанная лестницы содержат перилимфу, а улитковый проток заполнен эндолимфой. Эти жидкости различаются по химическому составу.
Границу между улитковым протоком и барабанной лестницей образует основная мембрана, на которой находится собственно сенсорный аппарат – кортиев орган. В кортиевом органе лежат рецепторные клетки. Они являются вторичными сенсорными клетками, т.к. у них нет аксонов. Тела клеток, передающих возбуждение от этого органа к центральной нервной системе, находятся в спиральном ганглии, который лежит в улитке, завиваясь вокруг ее оси вместе с каналами. В медицинской литературе принято различать звукопроводящий и звуковоспринимающий аппарат (рис.3.4.).
Рис.3.4. Структура органов слуха человека
87
Звукопроводящий аппарат включает наружное ухо и систему среднего уха (барабанная перепонка, слуховые мышцы, евстахиева труба, пещера с воздухоносными клетками височной кости и лабиринтные окна), перилимфу, эндолимфу и мембрану улитки. Звуковоспринимающий аппарат включает рецепторы (кортиев орган), проводящие пути и корковый центр.
Воздушные колебания по звукопроводящей системе передаются на рецепторы, а в них происходит трансформация звуковой энергии в процесс нервного возбуждения участков головного мозга [20].
3.4.2. Модели наружного и среднего уха
Наружное ухо служит в основном для придания слуху определенной направленности, концентрации энергии звуковых волн и защиты барабанной перепонки от вредных влияний изменяющейся температуры и влажности среды. На информационные процессы моноуральной обработки акустических сигналов оно не оказывает существенного влияния.
В [21] предлагается исследовать неравномерность частотной характеристики наружного уха, используя простейшую аппроксимацию его передаточной функции вида
Kн.у( p) = |
1 |
+ pT1 |
+ p2T02 |
(3.31) |
1 |
+ pT2 |
2 2 , |
|
|
|
+ p T0 |
|
||
где T0 = 40 мс, T1 = 60 мс , |
T2 = 15 мс. |
|
||
Погрешности аппроксимации экспериментальной частотной характеристики наружного уха не превышает 2 дб.
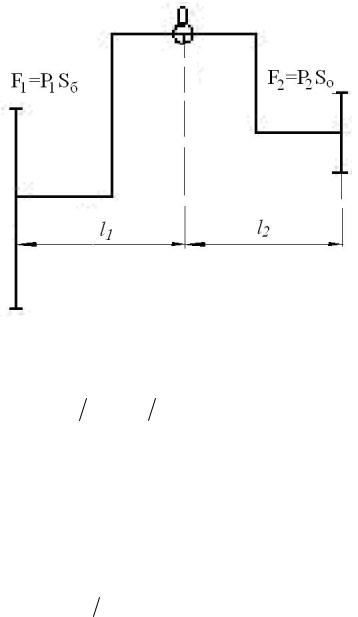
Основная роль среднего уха заключается в согласовании сопротивлений воздушной среды и перилимфы, заполняющей улитку внутреннего уха. Это согласование достигается при помощи системы подвижных косточек, которую в простейшей форме можно заменить одним рычагом
(рис.3.5).
Ввиду большой разности площадей барабанной перепонки и овального окна в структуре среднего уха происходит усиление звукового давления.
Сила F1 , действующая на плечо l1 рычага, определяется как произведение
давления P1 на площадь барабанной перепонки Sб : |
|
F1 = P1Sб. |
(3.32) |
Сила F2 , действующая на перилимфу внутреннего |
уха, зависит от |
площади овального окна: |
|
F2 = P2Sо. |
(3.33) |
Условие равновесия системы рычагов имеет вид |
|
F2l1 = F1l2. |
(3.34) |
88
Рис.3.5. Механическая модель среднего уха
Кроме того, скорость движения элементов на концах рычага связана с длиной его плеч соотношением
uб l2 =uо l1, |
(3.35) |
где uб и uо – скорости движения участков барабанной перепонки и овального окна соответственно.
Коэффициент преобразования сопротивления ( Z = P /u ) среднего уха можно найти с помощью формул (3-32)-(3-35).
|
Zб |
|
P1 |
|
uо |
2 |
|
(3.36) |
|||
|
|
|
= |
Sо |
|
l1 |
. |
|
|||
|
Zо uб P2 |
|
|
|
|||||||
|
|
Sб l22 |
|
||||||||
Используя значения l2 l1 =1,3; Sб = 0,55 см2 |
и S0 = 0.032 см2 , соответ- |
||||||||||
ствующие анатомическим данным, получаем Zо |
= 29Zб . |
||||||||||
Осуществляемое средним ухом согласование сопротивлений увеличивает передачу энергии звуковых колебаний в улитку приблизительно в 10 раз. При этом, по данным Звислоцкого, в улитку передается все же только 60% всей энергии, поступающей из воздушной среды.
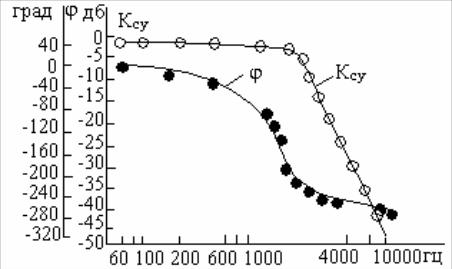
Представление о среднем ухе как о безынерционной системе рычагов справедливо лишь на частотах ниже 1 кГц. На более высоких частотах начинает сказываться инерционность элементов, вызывающая уменьшение коэффициента передачи среднего уха.
На рис. 3.6 приведены его частотные характеристики.
89
Рис.3.6. АЧХ и ФЧХ, полученные для модели среднего уха
Формула для коэффициента передачи среднего уха, выведенная Звислоцким, отражает всю сложность строения среднего уха и вследствие этого достаточно громоздка. Более компактной оказалась аппроксимация, предложенная Фаланганом:
Kс. у. = |
C0 |
|
|
, |
(3.37) |
( p +a)[( p −a)2 |
+b2 |
] |
|
||
|
|
|
где C0 – постоянная; b = 2a = 2π1500 рад/ с.
3.4.3. Модели улитки
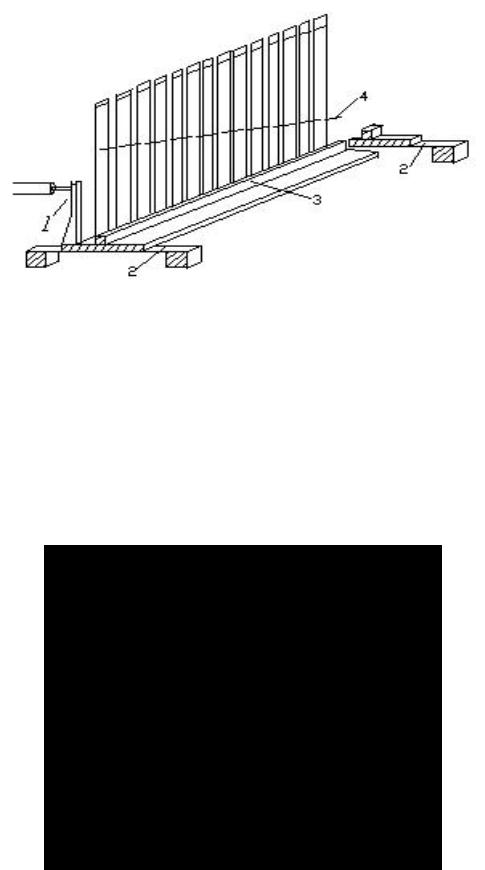
Современные работы по моделированию улитки ведутся на основе экспериментальных данных, полученных в работах лауреата Нобелевской премии 1961 г. Г. Бекеши. Он же является автором ряда первых механических и гидромеханических моделей, использующих механизм бегущей волны. Простейшая из рассмотренных им механических моделей улитки представляет собой некоторую модификацию язычкового частотомера
(рис.3.7).
В рассматриваемой модели ряд язычков с прогрессивно изменяющимися частотами собственных колебаний имитирует свойства, следующих друг за другом, элементарных участков основной мембраны. Возбуждение колебаний язычков осуществляется при помощи штока 1 через закрепленную на стальных пружинах 2 подставку 3. В отсутствие упругих связей между соседними язычками, как это имеет место в обычных частотомерах, модель работает так, как это следует из резонансной теории Гельмгольца, и бегущих волн в ней не возникает.
90
Рис.3.7. Язычковая модель колебательных процессов в улитке
Для создания режима бегущей волны между язычками должна быть введена упругая связь. Это достигается путем соединения язычков резиновой ленточкой. Лучшее приближение к колебательным характеристикам основной мембраны дает изменяющаяся вдоль ряда язычков связь. С этой целью резиновая ленточка укрепляется под некоторым углом к плоскости подставки, показанной на рис. 3.7 штриховой линией 4.
Существенно большей наглядностью обладает маятниковая модель улитки (рис.3.8), у которой весьма низкие частоты собственных колебаний маятников позволяют визуально наблюдать характерные особенности распространения колебаний в неоднородной системе.
Рис. 3.8. Маятниковая модель колебательных процессов в улитке
91
Модель (рис.3.8) включает в себя ряд маятников 4, состоящих из нити с шариком на конце, подвешенных на общем вращающемся стержне 2. Длина нити каждого следующего маятника больше, чем у предыдущего, таким образом, частота собственных колебаний понижается от маятника к маятнику. Вся система маятников возбуждается при помощи жестко закрепленного на общем стержне тяжелого маятника 1, диск которого можно устанавливать на различной высоте, изменяя тем самым частоту его колебаний. Связи между соседними маятниками осуществлены короткими нитями, посередине которых укреплены маленькие шарики 3.
После приведения в колебание массивного маятника в течение нескольких секунд протекает переходный процесс, во время которого происходит распространение энергии в направлении от коротких маятников к длинным. Фазовые сдвиги колебаний отдельных маятников вызывают картину бегущих волн. Ясно проявляется различие скоростей бегущей волны и распространения энергии (нарастания амплитуд колебаний вдоль ряда маятников). В установившемся режиме огибающая амплитуд иллюстрирует амплитудно-координатную характеристику системы на данной частоте возбуждения. Ее можно зарегистрировать, фотографируя снизу шарики маятников с большей экспозицией. Опыт с принудительной остановкой группы маятников (при помощи рейки, подводимой к нитям) в начале или конце ряда доказывает, что передача возбуждения маятникам происходит в основном через межмаятниковые связи, а не через общий стержень, на котором все они подвешены.
Вязычковой и маятниковой моделях непрерывное изменение колебательных характеристик улитки вдоль ее длины отображено с помощью ряда простейших осцилляторов, обладающих отличными друг от друга частотами собственных колебаний. На этом же принципе строятся простейшие электрические модели улитки, изготовление и настройка которых не сопряжены с необходимостью выполнения точных механических работ.
Впростых электрических моделях улитки отдельные точки основной мембраны имитируются независимыми колебательными контурами, возбуждаемыми параллельно (рис.3.9). При этом комплексный коэффициент передачи каждого частотного канала выражается соотношением
K( jω) = |
|
1 |
. |
(3.38) |
1 |
+ jξ |
|
||
|
|
|
Если Q – добротность колебательного контура, то
|
|
1 |
(3.39) |
|
ξ = Q |
λ − |
|
, |
|
λ |
|
|||

92
и при резонансной частоте колебательного контура ω0 относительная частота выходного сигнала λ = ω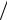 ω0 .
ω0 .
|
Для |
исключения |
взаимного |
|||
|
влияния отдельных цепей, обу- |
|||||
|
словленного сильной частотной за- |
|||||
|
висимостью их входных сопротив- |
|||||
|
лений, |
источник |
возбуждающий |
|||
|
эдс должен иметь низкое внутрен- |
|||||
|
нее сопротивление. |
|
||||
|
При измерении напряжения на |
|||||
|
резисторах R (рис.3.9) амплитуд- |
|||||
|
но-частотная характеристика каж- |
|||||
|
дого контура получается симмет- |
|||||
|
ричной, с одинаковой крутизной |
|||||
|
обоих |
склонов |
(при |
добротности |
||
|
Q = 2 крутизна склонов достигается |
|||||
|
12 дб на октаву (рис. 3.10). Лучшее |
|||||
|
приближение |
к |
характеристикам |
|||
|
основной мембраны дает напряже- |
|||||
Рис. 3.9. Принципиальная схема |
||||||
ние с конденсатора колебательного |
||||||
простейшей электрической модели |
||||||
основной мембраны |
контура (рис. 3.10, кривая б). |
|||||
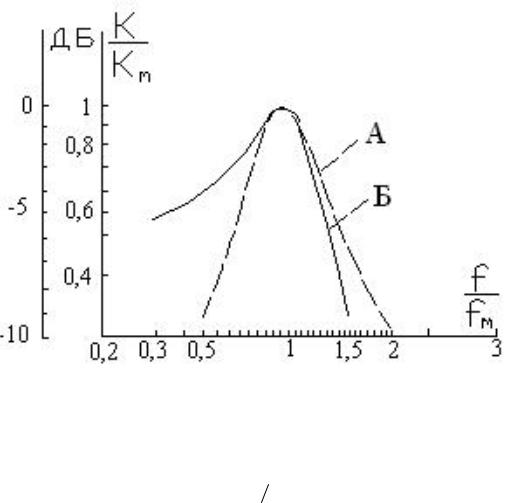
При этом крутизна склона амплитудно-частотной характеристики в сторону нижних частот уменьшается до 6 дб/окт, а в сторону верхних возрастает до 18 дб на октаву. Однако такая схема при низкой добротности колебательного контура обладает рядом особенностей.
Во-первых, частота максимума коэффициента передачи при малых добротностях (Q < 3) начинает отличаться от частоты резонанса f0 :
fm = f0 1 − |
1 |
(3.40) |
. |
||
|
2Q2 |
|
Эта зависимость представлена на рис. 3.11.
Во-вторых, при очень низких частотах коэффициент передачи контура перестает изменяться и стремится к постоянному значению K(0) = 1 . Максимальное же значение коэффициента передачи Km на частоте fm за-
висит от добротности: |
Q |
|
|
(3.41) |
||
Km = |
, |
|||||
|
|
|
||||
1 |
− |
|
1 |
|
|
|
4Q2 |
|
|||||
|
|
|
||||
и при Q < 1.31 оказывается меньше 1.41.
93
В последнем случае на левом склоне амплитудно-частотной характеристики отсутствует традиционная точка 0,7Km , по которой принято отсчитывать нижнюю границу полосы пропускания.
Рис. 3.10. АЧХ элементарных фильтров моделей (рис.3.6) при добротности Q = 2
В-третьих, если добротность Q определена обычным способом как отношение реактивного сопротивления к активному на резонансной частоте (именно это значение имеет символ Q во всех приводимых формулах):
Q =ω0 L R , |
(3.42) |
то отношение резонансной частоты к полосе пропускания перестает равняться значению Q . Расчетная зависимость полосы пропускания в долях
от резонансной частоты f0 показана на рис. 3.12 (кривая б).
Эти особенности амплитудно-частотных характеристик простейшей частотно-избирательной цепи с несимметричной формой резонансной кривой делают широко употребляемое понятие эквивалентной добротности основной мембраны весьма условным. В частности, оценка добротности по полосе пропускания на уровне 0,7:
Qэ = |
fm |
(3.43) |
f0,7 |
|
|
|
|
получается заниженной в сравнении с добротностью (3.42) колебательного контура в схеме рис. 3.9.

94
|
|
|
|
|
|
Рис.3.11. Относительное изменение частоты |
Рис. 3.12. Зависимость относительной |
|
максимума коэффициента передачи фильт- |
полосы пропускания на уровне 0,7 от |
|
ров модели на рис.3.9 в зависимости от их |
добротности для контуров, включен- |
|
добротности |
ных по схеме на рис. 3.9 |
|
С. Дейчем описана модель основной мембраны, состоящая из 21 колебательного контура (N=21) с резонансными частотами, образующими гео-
метрическую прогрессию со знаменателем  2 . Она позволяет исследовать характеристики мембраны на диапазон частот от 20 до 20370 гц. Значения емкости и индуктивности i -го контура составляют
2 . Она позволяет исследовать характеристики мембраны на диапазон частот от 20 до 20370 гц. Значения емкости и индуктивности i -го контура составляют
i−1
Ci = 2 2
|
i−1 |
|
0.0195 мкф; |
L = 2 2 |
0.031 гн. |
|
i |
|
Резисторы R1, R2 , ..., RN имеют одинаковые сопротивления (100 ом) и придают всем контурам добротность Q = 4 (в пренебрежении потерями в катушках самоиндукции, конденсаторах и на внутреннем сопротивлении источника сигнала).
Лучшее приближение к колебательным свойствам основной мембраны, описанным Бекеши, дали бы контуры с добротностью Q = 2,2 , для чего сопротивление резисторов надо увеличить до 180 ом.
В общем случае, выбирая полным диапазоном перекрываемых моделью частот
D = f1 fN |
(3.44) |
и частотный шаг соседних контуров
d = fi fi+1 , |
(3.45) |
можно найти необходимое число контуров путем округления до ближайшего целого числа величины
N = |
log D |
+1. |
(3.46) |
|
|||
log d |
|
||
|
|
|
Частота настройки i-го контура должна равняться
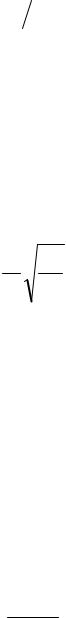
95 |
|
fi = f1 d i −1 . |
(3.47) |
Выбрав значения L1 и C1 для контура, настроенного на высшую часто- |
|
ту f1 , определяют соответствующие значения Li |
и Ci остальных контуров |
по формулам |
(3.48) |
Li = d i−1L1; |
|
Ci = d i−1C1. |
(3.49) |
Сопротивление резисторов рассчитывается по желаемому значению добротности и при равных добротностях всех контуров получается одинаковым, не зависящим от номера контура i.
Ri = |
1 |
Li |
(3.50) |
Q |
Ci |
. |
|
|
|
Модели основной мембраны, выполненные по схеме (рис.3.9), неточно передают форму амплитудно-частотной характеристики, но в еще большей мере они отличаются от оригинала фазочастотными характеристиками. Сдвиг фазы выходного напряжения этих моделей относительно возбуждающей эдс в зависимости от частоты показан на рис. 3.13 (кривые а и б).
Накопление фазы при изменении частоты от нуля до резонансной составляет π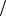 2 и при дальнейшем повышении частоты не превосходит π . Из данных Бекеши (например, кривая г на рис. 3.13) следует, что в основной мембране происходит значительно больший сдвиг фазы.
2 и при дальнейшем повышении частоты не превосходит π . Из данных Бекеши (например, кривая г на рис. 3.13) следует, что в основной мембране происходит значительно больший сдвиг фазы.
Создать избыточный сдвиг фаз можно с помощью линий задержки, вводимых между источником сигнала и частотными фильтрами. Необходимое время задержки в цепи каждого фильтра рассчитывается по формуле
τ= ϕiдоп ,
i2πfmi
где ϕiдоп – дополнительный сдвиг фазы на частоте fmi максимального отклика i-го канала.
Поскольку время задержки прогрессивно возрастает при понижении fmi (в направлении от овального окошка к геликотреме), вместо индивидуальных линий задержки для каждого канала уместно применить одну об-
щую линию задержки с N отводами для подключения следующих друг за другом по частоте фильтров.
Эта идея претворена в модели, предложенной Фланаганом.

96
Рис. 3.13. Фазочастотные характеристики: а и б – моделей, изображенных на рис. 3.6, в – модели Фланагана; г – основной мембраны улитки для точки с координатной частотой 150 гц (по Бекеши)
Вскоре после создания первых гидродинамических моделей улитки появилась одна из наиболее фундаментальных работ, заложивших теорию колебательных процессов в таких системах. Звислоцким было получено и приближенно решено описывающее их дифференциальное уравнение.
Основные предпосылки развитой теории сводились к положениям:
1)жидкость не сжимается;
2)сечение вестибулярного и тимпанального каналов не меняются вдоль улитки;
3)потери на трение при колебаниях основной мембраны одинаковы на протяжении всей улитки;
4)масса основной мембраны меньше влияет на характер колебаний, чем ее податливость, и в первом приближении ее можно не принимать во внимание.
При таких условиях изучаемая структура улитки имеет вид, приведенный на рис. 3.14.
С учетом предпосылок 1 и 2 уравнение, связывающее изменение плот-
ности потока частиц жидкости вдоль оси x с изменением |
ϑ элементар- |
||
ного объема ϑ в вестибулярном канале улитки, записывается в виде |
|||
S |
1 |
∂K1 = ϑ, |
(3.51) |
|
∂x |
|
|
где S1 – площадь поперечного сечения вестибулярного канала; K1 – объемная плотность потока частиц жидкости в нем.

97
Рис. 3.14. Схема модели улитки, использованная Завислоцким при выводе уравнений движения основной мембраны. Стрелками отмечено движение частиц перилимфы при вдавливании мембраны круглого окна
Дифференцирование по времени обеих частей уравнения (3.51) можно вывести соотношение, связывающее скорость U1 изменения числа частиц в
выделенном объеме вестибулярного канала со скоростью V изменения этого объёма:
S |
∂U1 |
=V , |
(3.52) |
|
|||
∂x |
|
||
|
|
|
где U1 = ∂K1 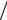 ∂t ; V = ∂( ϑ)
∂t ; V = ∂( ϑ)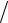 ∂t.
∂t.
Смещение элементов в структурах внутреннего уха под действием внешней силы описывается вторым законом движения Ньютона, с учетом которого уравнение (3.52) приводится к виду
S |
∂P1 |
= −ρS |
∂U1 |
− R S U |
, |
(3.53) |
1 |
∂x |
1 |
∂t |
1 1 1 |
|
|
где P1 – звуковое давление в вестибулярном канале; ρ – плотность перилимфы, заполняющей его; R1 – трение в перилимфе.
Дифференцируя (3.53) по x с учетом предпосылки 2, получим
|
∂P1 |
|
|
2 |
|
(3.54) |
|
S |
|
= −ρS ∂ |
|
U1 |
− R S ∂U1 . |
||
|
|
|
|||||
1 ∂x2 |
1 ∂x∂t |
1 1 ∂x |
|
||||
Используя выражение (3.52), получаем |
|
(3.55) |
|||||
|
S |
∂2 P1 = −ρ |
∂V |
− R V , |
|||
|
|
|
1 ∂x2 |
|
∂t |
1 |
|
где S2 – площадь поперечного сечения этого канала; |
P2 – звуковое дав- |
||||||

98
ление в нем; R2 – трение в перилимфе.
Давление P , действующее на единичный участок основной мембраны, равно разности давлений в вестибулярном и тимпанальном каналах:
Таким образом, |
|
|
|
|
P = P1 − P2 . |
|
|
|
|
(3.56) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.57) |
|||
∂2 P |
|
∂2 P1 |
|
∂2 P2 |
|
1 |
|
1 |
|
|
∂V |
|
R1 |
|
R2 |
|
|
∂x2 |
= |
∂x2 |
− |
∂x2 |
= − |
|
+ |
|
|
ρ |
|
− |
|
+ |
|
. |
|
|
S2 |
∂t |
S1 |
|
|
||||||||||||
|
|
S1 |
|
|
|
|
|
S2 |
|
||||||||
Подставляя выражение скорости изменения объема V через давление P и полное сопротивление
V = P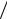 Z ,
Z ,
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.58) |
|
|
∂ |
2 |
P |
|
|
|
|
|
ρ |
|
∂P |
|
R1 |
|
|
|
P |
||
|
|
1 1 |
|
|
|
R2 |
|
||||||||||||
|
|
|
|
|
= − |
|
+ |
|
|
|
|
|
− |
|
+ |
|
|
|
. |
|
∂x |
2 |
|
|
Z |
|
∂t |
S1 |
|
Z |
|||||||||
|
|
|
S1 |
S2 |
|
|
|
S2 |
|
||||||||||
Обозначим
S = S1S2 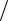 (S1 + S2 ) ;
(S1 + S2 ) ;
R S =(R1S2 + R2S1) (S1S2 ).
Тогда дифференциальное уравнение, связывающее изменение звукового давления P вдоль основной мембраны с его зависимостью от времени, принимает окончательный вид
∂ |
2 |
P |
|
ρ ∂P |
|
R |
(3.59) |
||
|
= − |
− |
P. |
||||||
∂x2 |
|
|
|
||||||
SZ ∂t |
SZ |
||||||||
|
|
|
|||||||
Если рассматривать только установившийся режим колебаний под действием гармонического колебания звукового давления, то, вводя в уравнение (3.29) комплексную амплитуду давления P( jω) , получаем обыкновенное дифференциальное уравнение
d |
2 |
P( jω) |
(3.60) |
||
|
= − |
R + jωρ |
P( jω). |
||
|
|
dx2 |
|
||
|
|
|
SZ(x) |
||
Его решение P(x) описывает распределение амплитуд и фаз давления вдоль основной мембраны для гармонического возбуждения заданной частоты. Полное сопротивление Z (x) определяется параметрами основной мембраны и в общем виде должно отражать активные потериупругость и
массу: |
|
1 |
(3.61) |
|
|
|
|||
Z = r + j |
ωm − |
|
, |
|
|
|
|||
|
|
ωc |
|
|
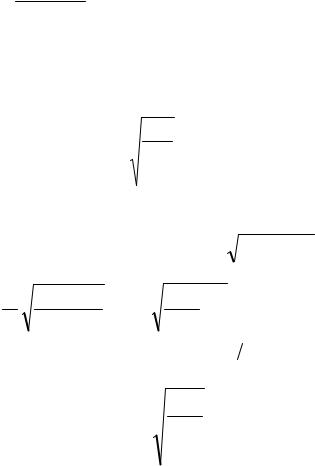
99
где r, m и c – погонные сопротивления потерь, масса и податливость основной мембраны. Однако в силу предпосылки 4 величиной m уместно пренебречь.
В принципе все параметры улитки зависят от координаты x , но наибольшую зависимость проявляет податливость основной мембраны c .
С учетом сделанных замечаний в первом приближении уместно рассмотреть вместо (3.59) уравнение, в котором только один параметр c зависит от координаты:
∂2 P( jω) + ( jωρ +
∂x2 S r +
R)P( jω) |
(3.62) |
|
= 0. |
||
1 |
|
|
|
|
|
|
|
|
|
|
|
jωc(x) |
|
|
Аппроксимируя зависимость |
c(x) |
выражением |
c = c eβx , |
можно по- |
|||||||||||||||||||
|
|
|
|
|
0 |
|
|||||||||||||||||
лучить следующее приближенное решение этого уравнения: |
|
(3.63) |
|||||||||||||||||||||
|
|
|
P( jω, x) = B |
|
x |
|
|
|
)H02 (γA ), |
|
|
||||||||||||
|
|
|
th |
x (1 |
+ |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где H02 – функция Бесселя третьего рода; B – произвольная постоянная, |
|||||||||||||||||||||||
|
|
−2 |
|
x2 |
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
≈ |
10 |
|
|
|
|
|
+ |
|
|
; |
= 2arcsh jωrc f βx ; |
|
|
|
|||||||||
|
|
2 |
|
|
3 |
|
|
|
|||||||||||||||
|
|
|
|
A |
|
|
A |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
A = |
1 jωρ + R ; γ = |
|
1 |
|
|
|
−1. |
|
|
|
|
||||||||||||
|
β |
|
|
|
r |
|
|
|
|
|
|
6 A2 |
|
|
|
|
|
|
|||||
При не слишком больших отношениях A значение |
|
мало и вместо |
|||||||||||||||||||||
(3.63) имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.64) |
|
|
|
|
|
|
|
P(x) = B |
|
|
x |
H0(2) (γA ). |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
th |
x |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Найдем выражение комплексного коэффициента передачи улитки |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
K у ( jω, x) = |
Y ( jω, x) |
, |
|
|
|
(3.65) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y0 ( jω) |
|
|
|
|
|
где Y ( jω, x) – амплитуда колебаний основной мембраны в точке x ; Y0 –
амплитуда колебаний стремечка: |
|
|
|
|
||||
Y ( jω, x) = |
P( jω, x) 1 |
и |
Y0 ( jω) = |
P( jω,0) |
. |
|||
|
|
|
|
|||||
Z(x) jω |
||||||||
|
|
|
r jω |
|||||
|
|
|
|
|
|
вх |
||
Принципиально иной подход к описанию свойств улитки проявил ряд авторов, стремившихся получить точные и в то же время достаточно про-

100
стые аналитические выражения ее частотных и координатных характеристик. В этом подходе игнорируются анатомические и физиологические данные о природе механизмов, формирующих изучаемые характеристики, а для описания последних используется метод аналитической аппроксимации экспериментальных данных. Наибольшую известность получили аппроксимации частотной зависимости комплексного коэффициента передачи улитки, предложенные Фланаганом. Одна из последних модификаций формулы Фланагана имеет вид
K у ( p) = A(β) |
p +0,1β |
|
1 |
|
e− pτ . |
(3.66) |
|
|
|||||
p + β [( p +0,5β)2 + β 2 |
]2 |
|
||||
|
|
|
||||
Здесь β = 2πfx – частота, вызывающая максимальный отклик в данной точке основной мембраны; A(β) – скалярный множитель; τ – параметр,
имитирующий задержку времени за счет пробега волны от овального окна до рассматриваемой точки основной мембраны:
τ = 43πβ .
Связь координаты точки x основной мембраны с частотой, вызывающей наибольшие колебания, описывается формулой Гринвуда
|
− |
a |
(l −x) |
|
(3.67) |
|
|||||
|
|
M |
|
|
|
fx = b e |
|
|
|
−1 , |
|
|
|
|
|
|
|
где b =165,4 гц; a = 0,06 1/мм; l = 35 |
мм; M = 0,43429. |
|
|||
На рис.3.15 представлены амплитудно-частотная и фазочастотная характеристики, выражаемые формулой (3.66).
С учетом этих данных можно изменить аппроксимационную формулу Фланагана (3.66) так, чтобы в области нижних частот она совпадала с данными Бекеши, а в области верхних частот – с результатами последних исследований.
Модифицированная таким образом формула имеет вид
K у(γ ) = |
|
Aγ |
|
, |
(3.68) |
|
+γ 2 )m (1 −γ 2 |
+γ 4 )n |
|
||
(1 |
|
|
|||
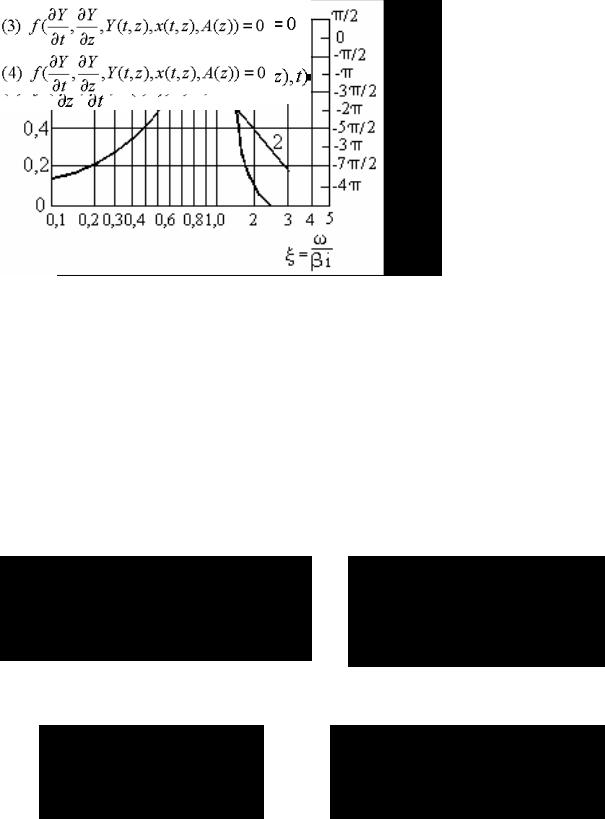
где γ = f 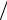 f0 ; f0 = 0,94 fx1,05 ;
f0 ; f0 = 0,94 fx1,05 ;
m = −0,485 10−8 f02 +0,295 10−3 f0 +0,175; n = −0,735 10−8 f02 +0,54 10−3 f0 +0.725;
fx – частота синусоидального сигнала, в ответ на который данная точка основной мембраны улитки колеблется с максимальной амплитудой;
101
f – частота воздействующего сигнала.
Рис.3.15. АЧХ (1) и ФЧХ (2), вытекающие из формулы (3.66), аппроксимирующей коэффициент передачи основной мембраны улитки органа слуха; по оси абсцисс отложена нормированная частота
Из формулы (3.68) следует, что в области высоких частот крутизна и добротность амплитудно-частотных характеристик улитки оказываются выше, чем при расчете по формулам Фланагана.
Контрольные вопросы
31)Какие из приведенных уравнений являются моделями статики?
32)Какие уравнения являются моделями динамики нестационарного объекта с сосредоточенными координатами?
33)Какое уравнение описывает модель идеального вытеснения?
102
34)Какое уравнение соответствует модели идеального смешения?
35)Допущения модели идеального смешения.
36)Допущения модели идеального вытеснения.
37)Какие интерпретации вектора входных и выходных координат объекта моделирования вы знаете ?
38)Какие допущения использованы при построении гидродинамической модели улитки ?
39)Приведите примеры стационарных моделей органов слуха.
40)Какие допущения использованы в модели газообмена в системе внешнего дыхания человека ?
41)Как используются допущения об идеальном смешении при построении модели органов дыхания ?
42)Приведите примеры стационарных моделей, описывающих биологический объект с сосредоточенными координатами,
43)Приведите примеры стационарных моделей с распределенными координатами, описывающих биологический объект.
44)Перечислите составляющие вектора Х и вектора Y для модели газообмена в системе внешнего дыхания человека.
45)Составьте блок-схему исследуемого объекта на основе электрической модели мембраны улитки.
46)Приведите примеры коррекции математических моделей путем последовательного уточнения уравнений (на примерах моделей органов слуха).
