5.1. Сетевое моделирование

Наиболее часто в области сетевого моделирования рассматриваются две задачи, связанные с сетями: задача о кратчайшем пути и задача о максимальном потоке. Например, если в роли взвешенного орграфа выступает сеть нефтепроводов, то при решении задачи о максимальном потоке нефти через эту сеть веса, данные в скобках рядом с дугами, указывают на скорость потребления нефти и пропускную способность труб. Вершины такого орграфа представляют собой потребителей или производителей нефти, а дуги - нефтепроводы.

В случае если решается задача о кратчайшем пути, веса дуг графа задаются расстоянием между вершинами, которые эти дуги соединяют. Пусть, например, имеется топологическая карта транспортной сети из 5 дорог, соединяющих 4 населённых пункта, причём необходимо выбрать кратчайший путь из пунктаx₁ в пункт x₄:

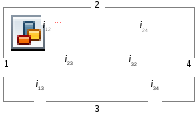
Рис. 17. Топологическая карта транспортной сети из 5 ветвей

Оказывается, используя аналогию между длиной пути U_ij между пунктами i и j и электрическим напряжением Ūij между точками i и j электрической цепи, можно решать задачу о кратчайшем пути, моделируя транспортную сеть Рис. 17 следующей электрической схемой:

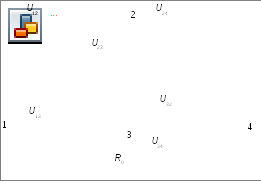
Рис. 18. Электрическая модель транспортной сети Рис. 17.

Впрочем, любая электрическая схема сама по себе представляет ориентированный и взвешенный граф. Ориентированным граф будет в силу протекающих в определённом направлении токов по разным участкам схемы. Величины токов могут играть роль весов соответствующих дуг графа, а величины напряжений - роль весов соответствующих вершин графа. Свойство постоянства потока в сети равносильно высказыванию о том, что поток в промежуточной вершине не исчезает и не возникает. Это свойство эквивалентно закону Кирхгофа для цепи постоянного тока.

Моделируя сетевые структуры, следует различать некоторые разновидности графов с экстремальными характеристиками и учитывать связанные с ними понятия. Простой цепью (а) называется граф, у которого только две вершины имеют степень, равную единице, а остальные – степень, равную двум. Цикл (б) есть граф, все вершины которого имеют степень, равную двум. Число вершин в цикле называется его длиной.

Рис. 19. Цепь (а) и цикл (б) в ориентированном графе.

Цикл и цепь задаются последовательностью вершин и рёбер, входящих в них. Граф, все вершины которого попарно смежные, называется полным. Граф, все вершины которого попарно несмежные, называется пустым. Граф называется связным, если для любых вершин X_i, X_j существует цепь, которой принадлежат вершины X_i и X_j .

Компонентом связности графа (а) является подграф (б):

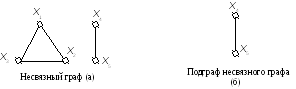
Связный граф на n вершинах с минимальным числом рёбер называется деревом.

В теории графов транспортной сетью называется ориентированный связной мультиграф без петель, в котором:

1. Существует одна и только одна такая вершина х₁ называемая входом сети, что g ^-1(x₁) = 0;

2. Существует одна и только одна такая вершина х_n, называемая выходом сети, что g (x_n) = 0

3. Каждой дуге U графа соответствует некоторое число K(U) ≥ 0, называемое пропускной способностью дуги.

Потоком f(U) транспортной сети называется некоторая функция f(U), определённая на множестве дуг графа и удовлетворяющая свойствам:

1. f(U) ≥ 0

2. u Î U_x^- ∑ f(U) – u Î U_x⁺ ∑ f(U) = 0 (x ¹ x₁, x ¹ x_n)

3. f(U) £ K(U); u Î U, где U_x^-, U_x⁺ - множество дуг, входящих в вершину X и выходящая из неё.

Для иллюстрации методов сетевого моделирования рассмотрим задачу о максимальном потоке более подробно. Введем несколько обозначений.

1. Сеть с пропускной способностью (N, k) состоит из N узлов i, j. Упорядоченная пара узлов (i, j) называется дугой сети. Каждой дуге (i, j) приписывается определенная пропускная способность k(i, j).

2. Потоком в сети (N,k) называется функция f, сопоставляющая каждой дуге (i,j) число f(i,j) и обладающая свойствами:

f(i,j) = - f(i,j) и f(i,j) < k(i,j). Пропускная способность и поток может характеризовать как отдельную дугу, так и всю сеть (N, k).

3. Узел а множества N называется источником потока f, если f(s, N) > 0. Узел a' называется стоком, если f(s', N) < 0. Поток с одним источником я и одним стоком а' называется потоком от s к s'. Узлы s и s' связаны сложной промежуточной сетью N.

Метод нахождения максимального потока проиллюстрируем на примере некоей гипотетической водопроводной сети, схематически представленной в виде ориентированного графа, приведенного ниже.

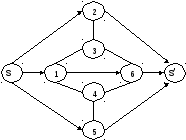
Рис. 20. Исходная сеть, исследуемая на предмет пропускной способности.

Числа при дугах указывают на пропускные способности соответствующих отрезков сети (в условных единицах). В соответствии с теорией графов, для удобства моделирования исходная исследуемая сеть (рис. 20) представляется матрицей пропускных способностей || k || (Табл. 1).

Таблица 1.

	s	1	2	3	4	5	6	s’
s	0	1	4	0	0	4	0	0
1	1	0	0	1	1	0	2	0
2	4	0	0	2	0	0	0	1
3	0	1	2	0	0	0	3	0
4	0	1	0	0	0	3	1	0
5	4	0	0	0	3	0	0	1
6	0	2	0	3	1	0	0	6
s’	0	0	1	0	0	1	6	0

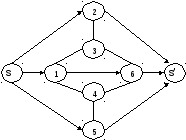
В этой матрице величина элемента i, j соответствует пропускной способности дуги (i, j). Для начала насыщения исходной сети возьмем поток f₁ = 3, который слагается из вытекающих во всех направлениях из источника s условных единиц потока, и соответствующую ему матрицу потока || f₁ ||. Эта матрица || f₁ ||. вместе с ориентированным графом, соответствующим потоку f₁, изображены ниже:

	S	1	2	3	4	5	6	s’
s		1	1			1
1	-1						1
2	-1							1
3
4
5	-1							1
6		-1						1
s’			-1			-1	-1

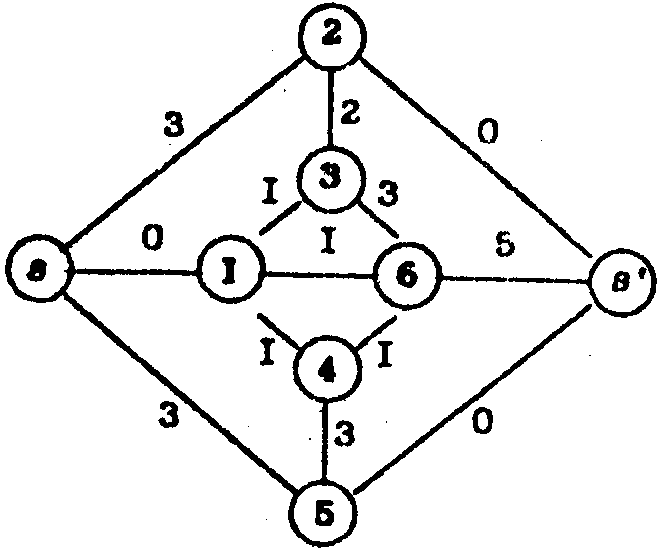
Знаки (-) в матрице || f₁ || возникли в силу свойства № 2 определения потока. Теперь, чтобы выяснить, насколько полно поток f₁ насыщает исходную сеть, вычтем f₁ из k, а также соответствующие этим потокам матрицы и получим новую сеть k₁ = k – f₁ и новую матрицу пропускных способностей || k₁ || = || k || – ‌‌|‌‌‌ | f₁ ||:

	s	1	2	3	4	5	6	s’
s		0	3			3
1	2			1	1		1
2	5			2				0
3		1	2				3
4		1				3	1
5	5				3			0
6		3		3	1			5
s’			2			2	7

Появление в матрице || k₁ || нулей говорит о появлении насыщенных дуг (s,1), (2,s') и (5,s') в результате операции вычитания. Найдем те узлы, которых можно достичь из (а), следуя по ненасыщенным дугам. Эти узлы определяются положительными элементами первой строки матрицы || k₁ ||, т.е. это узлы (2) и (5). Из узлов (2) и (5) достижимы узлы (3) и (4) , из узлов (3) и (4) можно попасть в узел (6), а из него – (s').

Таким образом, одним из ненасыщенных путей является путь (s,2), (2,3), (3,6), (6,s'). Образующие этот путь элементы в матрице || k₁ || обведены кружками, а элементы в квадратиках образуют путь для потока в противоположном направлении. Минимальная пропускная способность пути (s,2), (2,3), (3,6), (6,s') лимитируется дугой (2,3), значит, по нему возможен поток мощностью максимум 2 единицы. Обозначив этот поток f₂ = 2, вычтем из его сети k₁. Новую матрицу пропускных способностей || k₂ || = || k₁ || - || f₂ || получим вычитанием 2 из элементов || k₁ ||, обведенных кружками, и добавлением 2 к элементам, обведённым квадратами. Вот эта матрица || k₂ ||:

	s	1	2	3	4	5	6	S’
s		0	3			3
1	2			1	1		1
2	7			0				0
3		1	4				1
4		1				3	1
5	5				3			0
6		3		5	1			3
s’			2			2	9

Еще один ненасыщенный путь из (s) в (s’) образован дугами (s,5), (5,4), (4,6), (6,s'). Он отмечен кружками в матрице || k₂ ||, а обратный путь - квадратами. Минимальное сечение этого пути лимитируется дугой (4,6) и равно 1, а значит, максимальный поток по этому пути f₃ = 1. Новую матрицу пропускных способностей || k₃ || = || k₂ || - || f₃ || получим, таким образом, как ранее || k₂ ||, в виде следующей таблицы:

	s	1	2	3	4	5	6	s’
s		0	1			2
1	2			1	1		1
2	7			0				0
3		1	4				1
4		1				4	0
5	6				2			0
6		3		5	2			2
s’			2			2	10

Единственный оставшийся ненасыщенным путь из (s) в (s’) отмечен кружками в матрице ||k₃||. Это путь (s,5), (5,4), (4,1), (1,6), (6,s'). Максимальный поток f₄ = 1 по этому пути лимитируется дугами (4,1) и (1,6). Производя снова операцию вычитания потока f₄, получим последнюю матрицу пропускных способностей ||k₄|| = || k₃ || - || f₄ ||:

Таблица 2.

	s	1	2	3	4	5	6	s’
s		0	1			1
1	2			1	2		0
2	7			0				0
3		1	4				1
4		0				5	0
5	7				1			0
6		4		5	2			1
s’			2			2	11

Выделенные кружками узлы, которых можно достичь, исходя из (s), не включают узел (s’). Значит, невозможно более никакого потока в этой сети. Полный поток, насыщающий исходную сеть k (рис.20), слагается из найденных частичных потоков:

f_макс = f₁ + f₂ + f₃ + f₄ = 3 + 2 + 1 + 1 = 7.

Матрицу максимального потока || f_макс || = || k || - || k₄ || получим вычитанием последней матрицы пропускных способностей (Табл. 2) из исходной матрицы (Табл.1):

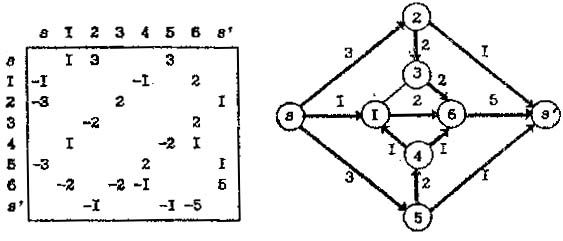
Рис. 21. Матрица || f_макс || и соответствующий ей поток f_макс.

Полный поток, вытекающий из (s), равный сумме элементов первой строки || f_макс ||, равен полному стоку в (s’), т. е. сумме элементов последнего столбца, и оказывается равным 7 условных единиц. Интересно отметить, что отсутствует вклад дуги (1,2) в полный поток, хотя она обладает единичной пропускной способностью.