
- •Содержание Двойной и тройной интегралы.
- •1 Двойной интеграл. Объем цилиндрического тела.
- •2 Свойства двойных интегралов
- •3 Вычисление двойного интеграла
- •4 Двойной интеграл в полярных координатах
- •5 Вычисление площади поверхности
- •6 Вычисление площадей и объёмов посредством двойного интеграла
- •7. Тройной интеграл
- •8. Физические приложения двойных и тройных интегралов
- •Криволинейные интегралы первого и второго рода.
- •1 Криволинейный интеграл второго рода по координатам
- •2 Вычисление криволинейного интеграла по координатам
- •3 Криволинейный интеграл первого рода (по длине дуги)
- •4 Основные свойства криволинейного интеграла первого рода
- •5. Формула Грина.
- •7 Поверхностные интегралы
- •8 Вычисление поверхностного интеграла
- •9 Формула Стокса
- •Элементы теории поля.
- •1 Скалярное поле. Производная по направлению. Градиент
- •2 Векторное поле. Поток и дивергенция поля
- •3 Циркуляция и ротор векторного поля
- •4. Оператор Гамильтона и его применение.
- •Дифференциальные уравнения
- •1. Основные понятия. Дифференциальные уравнения с разделяющимися переменными.
- •2. Однородные уравнения
- •5. Интегрирование дифференциальных уравнений высших порядков.
- •6. Составление дифференциального уравнения по заданной фундаментальной системе решений.
- •7. Линейные неоднородные уравнения с постоянными коэффициентами. Метод подбора.
- •8. Уравнение Эйлера
- •9. Линейные системы дифференциальных уравнений с постоянными коэффициентами
- •Теория функций комплексного переменного.
- •1. Комплексные числа
- •2. Непрерывные функции комплексного переменного
- •3. Дифференцирование функций. Условие Коши-Римана.
- •4 Сопряжённые гармонические функции
- •5 Конформное отображение
- •6 Постоянство растяжений
- •7 Интеграл по комплексному переменному
- •8 Ряд Лорана
- •9 Классификация изолированных особых точек
- •10 Вычеты
- •11. Вычисление интегралов при помощи вычетов
- •12. Вычисление интегралов, содержащих показательную функцию
- •13. Задачи по Теории Функции Комплексного Переменного
6. Составление дифференциального уравнения по заданной фундаментальной системе решений.
Рассмотрим
линейно-независимую на
 систему функций
систему функций (1), имеющих производные доn-го
порядка включительно.
(1), имеющих производные доn-го
порядка включительно.
 (2)
(2)
Где
 - неизвестная функция будет линейным
дифференциальным уравнением , для
которого функции (1) составляют
фундаментальную систему решений .
Коэффициенты приn-ой
производной в (2) есть
- неизвестная функция будет линейным
дифференциальным уравнением , для
которого функции (1) составляют
фундаментальную систему решений .
Коэффициенты приn-ой
производной в (2) есть
 системы (1).
системы (1).
Те
точки, в которых этот определитель
обращается в ноль, называются особыми
точками построенного уравнения. В этих
точках обращается в ноль коэффициент
при старшей производной
 ,
для которой функции
,
для которой функции и
и образуют фундаментальную систему
решений.
образуют фундаментальную систему
решений.




7. Линейные неоднородные уравнения с постоянными коэффициентами. Метод подбора.
Для правых частей специального вида частные решения находятся так


Где
 и
и - многочлены степениl
и m
соответственно.
- многочлены степениl
и m
соответственно.
В этом
случае


 и
и
 - многочлены отx,
k-ой
степени общего вида с неопределенными
коэффициентами
- многочлены отx,
k-ой
степени общего вида с неопределенными
коэффициентами

Если
 не является корнем характеристического
уравнения тоs=0.
не является корнем характеристического
уравнения тоs=0.
 (1)
(1)
Если
 ,
то на рассматриваемом интервале после
деления будем иметь
,
то на рассматриваемом интервале после
деления будем иметь
 (2)
(2)

Если
 в уравнении (1) все коэффициенты
в уравнении (1) все коэффициенты и правая часть
и правая часть непрерывны, то оно имеет единственное
решение при
непрерывны, то оно имеет единственное
решение при

где
 - любые действительные числа, а
- любые действительные числа, а - любая точка
- любая точка .
.
Действительно
 (1a)
(1a)
В окрестности рассматриваемых начальных значений удовлетворяет условиям теоремы существования и единственности
Имеет
ограниченные частные производные, где
 ,
т.к. эти производные равны непрерывным
коэффициентам
,
т.к. эти производные равны непрерывным
коэффициентам .
На начальные значения
.
На начальные значения не налагается никаких ограничений
не налагается никаких ограничений
1.
2.
В первом случае С – постоянная.
 ,
а
,
а

Доказательство
 здесь
здесь
 ,
а
,
а
Если
 является решением уравнения
является решением уравнения



 ,
где
,
где
 - постоянные.
- постоянные.
Доказательство
 (3)
(3)


Это
свойство, называемое принципом
суперпозиций, остается справедливым и
при
 если ряд
если ряд сходится и допускаетсяn-кратное
почленное дифференцирование.
сходится и допускаетсяn-кратное
почленное дифференцирование.
В этом
случае возможен переход в (3).Если
 все коэффициенты
все коэффициенты - функции
- функции и
и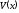 действительны, имеют решения
действительны, имеют решения ,
то действительная часть
,
то действительная часть и мнимая часть
и мнимая часть являются соответствующими решениями
уравнений
являются соответствующими решениями
уравнений и
и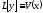
Теорема
Общее
решение на
 уравнения
уравнения с непрерывными на том же отрезке
коэффициентами
с непрерывными на том же отрезке
коэффициентами и правой частью
и правой частью равно сумме общего решения соответствующего
однородного уравнения и
равно сумме общего решения соответствующего
однородного уравнения и неоднородного уравнения.
неоднородного уравнения.
Метод подбора со специальным видом правой части.
Пусть имеется дифференциальное уравнение
 (1)
(1)
1.
 - многочлен n-ой
степени, тогда
- многочлен n-ой
степени, тогда
1)
 не является корнем характеристического
уравнения
не является корнем характеристического
уравнения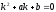
здесь
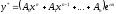 (3)
(3)

 - многочлен степени
n.
- многочлен степени
n.
 - многочлен степени
n-2.
- многочлен степени
n-2.
Слева
и справа имеем многочлен n-ой
степени. Приравнивая коэффициент, при
равных степенях n
, получаем систему для нахождения

Пример












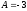



2) является однократным корнем
характеристического уравнения
является однократным корнем
характеристического уравнения

Пример













3) -
двукратный корень характеристического
уравнения
-
двукратный корень характеристического
уравнения

Пример











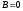

Правило 1
Если
правая часть
 уравнения есть произведение показательной
функции
уравнения есть произведение показательной
функции на многочлен
на многочлен ,
то частное решение уравнения следует
искать в виде
,
то частное решение уравнения следует
искать в виде
 - многочлен n-ой
степени с неопределенными коэффициентами,
а показатель степени
- многочлен n-ой
степени с неопределенными коэффициентами,
а показатель степени
 равен кратности корня
равен кратности корня в характеристическом уравнении.
в характеристическом уравнении.
Правило 2.
Если
правая часть
 есть многочленn-ой
степени
есть многочленn-ой
степени
 ,
то частное решение такого уравнения
,
то частное решение такого уравнения ,
где
,
где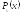 - многочленn-ой
степени с неопределенными коэффициентами
- многочленn-ой
степени с неопределенными коэффициентами
 показатель степени
показатель степени равен кратности корня
равен кратности корня
Пример









 | 12A = 1
| 12A = 1

 | 6A+8B=0
| 6A+8B=0

 |
2B+4C=0
|
2B+4C=0



Если
правая часть

 и
и
 -
многочлены
-
многочлены


 и
и
 -
многочленыk-ой
степени общего вида с неопределёнными
коэффициентами
-
многочленыk-ой
степени общего вида с неопределёнными
коэффициентами
 -
кратность корней
-
кратность корней
 характеристического уравнения, где
характеристического уравнения, где не является корнем характеристического
уравнения
не является корнем характеристического
уравнения
Пример





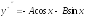

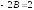

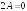


Сводная таблица видов частных решений для различных видов правых частей.
|
Правая часть дифференциального уравнения |
Корни характеристического уравнения |
Виды частных решений |
|
|
1. Число 0 не является корнем характеристического уравнения |
|
|
2.
Число 0 корень характеристического
уравнения кратности
|
| |
|
|
1.
|
|
|
2.
|
| |
|
|
1.
|
|
|
2.
|
| |
|
|
1.
|
|
|
2.
|
|
Пример 1.



 ;
;















Пример 2.


 ;
;






 ;
;





 многочлен с
неизвестными коэффициентами
многочлен с
неизвестными коэффициентами


 не является корнем характеристического
уравнения
не является корнем характеристического
уравнения
 является корнем характеристического
уравнения кратности
является корнем характеристического
уравнения кратности


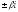 не является корнем характеристического
уравнения
не является корнем характеристического
уравнения
 является корнем характеристического
уравнения кратности
является корнем характеристического
уравнения кратности


 не является корнем характеристического
уравнения
не является корнем характеристического
уравнения
 является корнем характеристического
уравнения кратности
является корнем характеристического
уравнения кратности
