7. Тройной интеграл

Пределы интегрирования будут постоянными, если объемной областью, по которой берется интеграл, является куб или параллелепипед. Во всех других случаях пределы функциональны. Область интегрирования должна быть правильной, в случае, если она неправильная, её разбивают на ряд правильных областей и полученные результаты суммируют.

Тройной интеграл обладает свойствами аналогичными свойствам двойного интеграла.

Предположим, что f(x,y,z) определена и непрерывна в пространственной области V, ограниченной и, гдеиопределены и непрерывны в областиD, принадлежащей OXY. Тогда вычисление тройного интеграла сводится к последовательному интегрированию по переменной z (x и y являются при этом константами).

Пример 1

V: x = 0, y = 0, z = 0,

x + y + z = 1

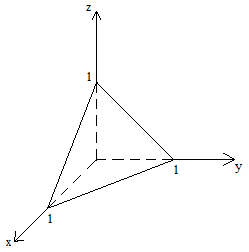
Пример 2

V: x = 1, y = 0, z = 2,

x = 3, y = 2, z = 5

Замена переменных

1. Тройной интеграл в цилиндрических координатах

Данную пространственную область V разбиваем на объемы поверхностями

Получаются круговые цилиндры, ось которых совпадает с осью z.

Площадь основания призмы (элементарного объема) , следовательно

(1)

Пример 1

V:

Пример 2

V:

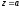
2. Тройной интеграл в сферических координатах

Пример 1

V: верхняя половина шара

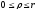
Пример 2

V:

8. Физические приложения двойных и тройных интегралов

Если пластина занимает область D плоскости OXY, имеет поверхностную плотность 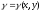, то масса пластины выражается так:

Если пластина однородная

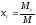
Моменты инерции пластины относительно OX и OY:

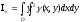
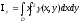
Полагая , получим формулы для вычисления моментов инерции плоского тела.

Пример

Найти координаты центра тяжести

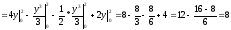
Криволинейные интегралы первого и второго рода.

1 Криволинейный интеграл второго рода по координатам

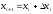
К точке приложена сила, которая меняется как по величине, так и по направлению. Вычислим работусилыпри перемещении точки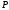из положенияв. Разобьём кривуюнаn произвольных частей.

в обозначим.

можно рассматривать как

и - проекциина осиOX и OY;

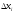и - приращение координат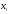ипри перемещении отк.

(1)

Если существует предел выражения в правой части при 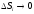,,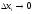, 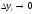то этот предел выражает работу силы:(2)

Формула (2) – криволинейный интеграл 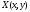ипо кривой

(3)

и стоящие вместо предела интегрирования заключены в скобки в знак того, что это обозначение кривой по которой берётся интеграл.

Направление 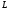откназывается направлением интегрирования.

- стоящая под знаком интеграла означает, что интеграл вдоль кривой.

Свойства криволинейных интегралов.

1. Криволинейный интеграл определяется подынтегральным выражением, формой кривой интегрирования и указанием направления интегрирования. При изменении направления интегрирования интеграл меняет знак, т.к. при этом , а следовательноименяют знаки.

2. . Это отношение справедливо для любого числа слагаемых.

Когда замкнута свойства остаются в силе.

Начальная и конечная точки совпадают.

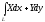или .

К понятию криволинейного интеграла приводит задача о работе на криволинейном пути. Во всех точках кривой была заданазависящая от точки приложения. Проекцией переменного вектора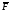на оси координат равно скалярному произведению.

можно рассматривать как интеграл от векторной функции заданной проекциямии.

Если , то интеграл будет равен криволинейному интегралу.

Если лежит на плоскости, то.

Когда криволинейный интеграл от векторной функции берётся по замкнутой кривой, то его называют циркуляцией векторапо замкнутому контуру.