
- •Содержание Двойной и тройной интегралы.
- •1 Двойной интеграл. Объем цилиндрического тела.
- •2 Свойства двойных интегралов
- •3 Вычисление двойного интеграла
- •4 Двойной интеграл в полярных координатах
- •5 Вычисление площади поверхности
- •6 Вычисление площадей и объёмов посредством двойного интеграла
- •7. Тройной интеграл
- •8. Физические приложения двойных и тройных интегралов
- •Криволинейные интегралы первого и второго рода.
- •1 Криволинейный интеграл второго рода по координатам
- •2 Вычисление криволинейного интеграла по координатам
- •3 Криволинейный интеграл первого рода (по длине дуги)
- •4 Основные свойства криволинейного интеграла первого рода
- •5. Формула Грина.
- •7 Поверхностные интегралы
- •8 Вычисление поверхностного интеграла
- •9 Формула Стокса
- •Элементы теории поля.
- •1 Скалярное поле. Производная по направлению. Градиент
- •2 Векторное поле. Поток и дивергенция поля
- •3 Циркуляция и ротор векторного поля
- •4. Оператор Гамильтона и его применение.
- •Дифференциальные уравнения
- •1. Основные понятия. Дифференциальные уравнения с разделяющимися переменными.
- •2. Однородные уравнения
- •5. Интегрирование дифференциальных уравнений высших порядков.
- •6. Составление дифференциального уравнения по заданной фундаментальной системе решений.
- •7. Линейные неоднородные уравнения с постоянными коэффициентами. Метод подбора.
- •8. Уравнение Эйлера
- •9. Линейные системы дифференциальных уравнений с постоянными коэффициентами
- •Теория функций комплексного переменного.
- •1. Комплексные числа
- •2. Непрерывные функции комплексного переменного
- •3. Дифференцирование функций. Условие Коши-Римана.
- •4 Сопряжённые гармонические функции
- •5 Конформное отображение
- •6 Постоянство растяжений
- •7 Интеграл по комплексному переменному
- •8 Ряд Лорана
- •9 Классификация изолированных особых точек
- •10 Вычеты
- •11. Вычисление интегралов при помощи вычетов
- •12. Вычисление интегралов, содержащих показательную функцию
- •13. Задачи по Теории Функции Комплексного Переменного
7 Поверхностные интегралы
В
прямоугольной системе координат
 задана некоторая область
задана некоторая область .
Пусть в области
.
Пусть в области задана некоторая поверхность
задана некоторая поверхность ,
ограниченная некоторой пространственной
линией
,
ограниченная некоторой пространственной
линией .
Относительно
.
Относительно будем предполагать, что в каждой её
точке
будем предполагать, что в каждой её
точке определено положительное направление
единичным вектором
определено положительное направление
единичным вектором ,
направляющие косинусы которого являются
непрерывными функциями координат точек
поверхности. Пусть в каждой точке
поверхности
,
направляющие косинусы которого являются
непрерывными функциями координат точек
поверхности. Пусть в каждой точке
поверхности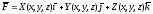 ,
где
,
где - непрерывные функции координат.
- непрерывные функции координат.
Разобьём
поверхность каким-либо способом на
элементарные площадки
 ,
на каждой площадке возьмём точку
,
на каждой площадке возьмём точку
 (1)
(1)
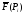 - значение вектора
- значение вектора
 в точке
в точке площадки
площадки .
.
 - единичный вектор
нормали в этой точке.
- единичный вектор
нормали в этой точке.
 - скалярное
произведение этих векторов.
- скалярное
произведение этих векторов.
Предел
суммы (1), распространённый на все
 при стремлении к нулю диаметров всех
таких площадок называется поверхностным
интегралом.
при стремлении к нулю диаметров всех
таких площадок называется поверхностным
интегралом.
 (2)
(2)
Каждое
слагаемое суммы (1)
 (3)
(3)
Механическое истолкование.
Это
произведение равно объёму цилиндра с
основанием
 и высотой
и высотой .
.
Если
 есть скорость жидкости, протекающей
через поверхность
есть скорость жидкости, протекающей
через поверхность ,
то произведение (3) равно количеству
жидкости протекающей через площадку
,
то произведение (3) равно количеству
жидкости протекающей через площадку за единицу времени в направлении вектора
за единицу времени в направлении вектора .
.
 даёт общее количество
жидкости протекающей в единицу времени
через поверхность
даёт общее количество
жидкости протекающей в единицу времени
через поверхность
 в положительном направлении, если под
в положительном направлении, если под подразумевать вектор скорости течения
жидкости в данной точке. Поэтому
поверхность интеграла (2) называется
потоком векторного поля
подразумевать вектор скорости течения
жидкости в данной точке. Поэтому
поверхность интеграла (2) называется
потоком векторного поля через поверхность
через поверхность .
.
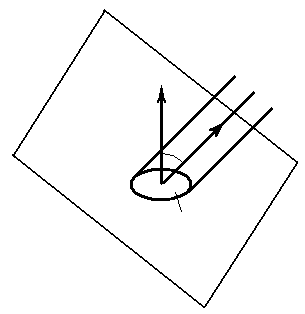
Из
определения поверхностного интеграла
следует, если
 разбить на части
разбить на части

Выразим
единичный вектор
 через его проекции на оси координат
через его проекции на оси координат

Подставляя
в (2) выражения
 и
и через их проекции, получим
через их проекции, получим

 - проекция площадки
- проекция площадки

 (4)
(4)

 .
.
8 Вычисление поверхностного интеграла
Вычисление интеграла по кривой поверхности сводится к вычислению двойного интеграла по плоской области.

Пусть
поверхность
 такова, что всякая прямая параллельная
такова, что всякая прямая параллельная пересекает её в одной точке.
пересекает её в одной точке.

Обозначим
через
 проекцию поверхности
проекцию поверхности на
на ,
получим
,
получим

 - интегральная
сумма для двойного интеграла по области
- интегральная
сумма для двойного интеграла по области
 от функции
от функции .
.

« + »
берётся, когда

« - »
берётся, когда

Если
 не удовлетворяет условию указанному в
начале, то её разбивают на части.
не удовлетворяет условию указанному в
начале, то её разбивают на части.


9 Формула Стокса
Пусть
имеется поверхность
 ,
такая, что всякая прямая, параллельная
,
такая, что всякая прямая, параллельная ,
пересекает её в одной точке. Границу
поверхности
,
пересекает её в одной точке. Границу
поверхности обозначим через
обозначим через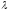 .
Положительное направление
.
Положительное направление возьмём таким образом, чтобы она
образовывала с положительным направлением
возьмём таким образом, чтобы она
образовывала с положительным направлением острый угол.
острый угол.

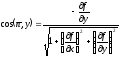


Предположим,
что
 всеми точками лежит в некоторой области
всеми точками лежит в некоторой области .
Пусть в
.
Пусть в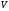 задана функция
задана функция ,
непрерывная вместе с частными производными
первого порядка.
,
непрерывная вместе с частными производными
первого порядка.
На
линии
 имеем
имеем ,
где
,
где -
координаты точек линии
-
координаты точек линии ,
являющейся проекцией линии
,
являющейся проекцией линии на
плоскость
на
плоскость .
.
 (2)
(2)
Сделаем преобразования по формуле Грина


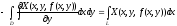 (3)
(3)
 (4)
(4)

 (5)
(5)
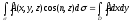

 (6)
(6)
Последний интеграл преобразуем с помощью (1).
 или
или

 (7)
(7)
 (8)
(8)
Направление
контура
 .
.
Если
наблюдатель смотрит с конца
 ,
то он видит обход против часовой стрелки.
,
то он видит обход против часовой стрелки.
Формула
(8) справедлива для любой поверхности,
если её можно разбить на части, уравнения
которой
 .
.
 (8a)
(8a)
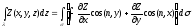 (8б)
(8б)

 (9)
(9)
(9) – формула Стокса.
Обход
по кривой
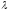 совершается по тому же правилу.
совершается по тому же правилу.
Теорема М.В.Остроградского(1801 - 1861).
Пусть
в пространстве задана правильная область
 ,
ограниченная замкнутой поверхностью
,
ограниченная замкнутой поверхностью ,
и проектируется на
,
и проектируется на в замкнутую область
в замкнутую область .
.
Предположим,
что
 можно разбить на 3 части
можно разбить на 3 части так, что уравнение первых двух
так, что уравнение первых двух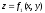
 .
.
Функции

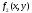 непрерывны в области
непрерывны в области ,
а третья часть - цилиндрическая поверхность
с образующими параллельными
,
а третья часть - цилиндрическая поверхность
с образующими параллельными .
.

 (1)
(1)
Выберем
на нормали к поверхности направление,
которое совпадает с направлением внешней
нормали к поверхности
 .
.
Тогда
 будет на поверхности
будет на поверхности положительным, а на
положительным, а на отрицательным, на
отрицательным, на он будет равен нулю. Двойные интегралы
в правой части (1) равны
он будет равен нулю. Двойные интегралы
в правой части (1) равны
 (2a)
(2a)

Элементы
поверхностей
 и
и и элемент площади
и элемент площади связаны
связаны ,
так как угол между
,
так как угол между и
и тупой.
тупой.
 (2б)
(2б)







