
- •Содержание Двойной и тройной интегралы.
- •1 Двойной интеграл. Объем цилиндрического тела.
- •2 Свойства двойных интегралов
- •3 Вычисление двойного интеграла
- •4 Двойной интеграл в полярных координатах
- •5 Вычисление площади поверхности
- •6 Вычисление площадей и объёмов посредством двойного интеграла
- •7. Тройной интеграл
- •8. Физические приложения двойных и тройных интегралов
- •Криволинейные интегралы первого и второго рода.
- •1 Криволинейный интеграл второго рода по координатам
- •2 Вычисление криволинейного интеграла по координатам
- •3 Криволинейный интеграл первого рода (по длине дуги)
- •4 Основные свойства криволинейного интеграла первого рода
- •5. Формула Грина.
- •7 Поверхностные интегралы
- •8 Вычисление поверхностного интеграла
- •9 Формула Стокса
- •Элементы теории поля.
- •1 Скалярное поле. Производная по направлению. Градиент
- •2 Векторное поле. Поток и дивергенция поля
- •3 Циркуляция и ротор векторного поля
- •4. Оператор Гамильтона и его применение.
- •Дифференциальные уравнения
- •1. Основные понятия. Дифференциальные уравнения с разделяющимися переменными.
- •2. Однородные уравнения
- •5. Интегрирование дифференциальных уравнений высших порядков.
- •6. Составление дифференциального уравнения по заданной фундаментальной системе решений.
- •7. Линейные неоднородные уравнения с постоянными коэффициентами. Метод подбора.
- •8. Уравнение Эйлера
- •9. Линейные системы дифференциальных уравнений с постоянными коэффициентами
- •Теория функций комплексного переменного.
- •1. Комплексные числа
- •2. Непрерывные функции комплексного переменного
- •3. Дифференцирование функций. Условие Коши-Римана.
- •4 Сопряжённые гармонические функции
- •5 Конформное отображение
- •6 Постоянство растяжений
- •7 Интеграл по комплексному переменному
- •8 Ряд Лорана
- •9 Классификация изолированных особых точек
- •10 Вычеты
- •11. Вычисление интегралов при помощи вычетов
- •12. Вычисление интегралов, содержащих показательную функцию
- •13. Задачи по Теории Функции Комплексного Переменного
8. Уравнение Эйлера
Уравнение
вида
 (1)
(1)
где
 - постоянные; называется уравнением
Эйлера.
- постоянные; называется уравнением
Эйлера.



Пример.

 ;
;






 ;
;
 ;
;





 ;
;


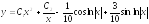
9. Линейные системы дифференциальных уравнений с постоянными коэффициентами







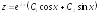


Этот метод называется методом сведения к уравнению соответствующего порядка. Порядок уравнения зависит от количества уравнений системы.
Пример 2.



 ;
;




 ;
;

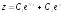


Пример 3

 -
характеристическое уравнение системы
-
характеристическое уравнение системы






1).








2).

3).










Теория функций комплексного переменного.
1. Комплексные числа

 - действительная
часть
- действительная
часть

 - мнимая часть
- мнимая часть



 называется
сопряженным комплексному числу
называется
сопряженным комплексному числу

Комплексные
числа
 и
и называются равными, если
называются равными, если и
и


 -
модуль комплексного числа
-
модуль комплексного числа



 - главное значение
- главное значение
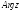


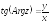


Два
комплексных числа
 и
и равны тогда и только тогда, когда их
модули равны, а их аргументы либо равны,
либо отличаются на величину, кратную
равны тогда и только тогда, когда их
модули равны, а их аргументы либо равны,
либо отличаются на величину, кратную .
.

Действия над комплексными числами
1.
2.
3.








При умножении комплексных чисел их модули перемножаются, а аргументы складываются

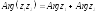







Формула Муавра

Свойства модуля комплексных чисел
1)
 2)
2)
 3)
3)
 4)
4)
 5)
5)

7)
 6)
6)

 8)
8)




Точки
соответствующих значений
 являются вершинами правильногоn
– угольника, вписанного в окружность
радиуса
являются вершинами правильногоn
– угольника, вписанного в окружность
радиуса
 с центром в начале координат. Любое
числоz,
не равное нулю, можно записать в
показательной форме
с центром в начале координат. Любое
числоz,
не равное нулю, можно записать в
показательной форме
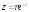 ,
где
,
где ,
, .
.
Формула Эйлера
 (a)
(a)


 (b)
(b)


2. Непрерывные функции комплексного переменного
Пусть на множестве E комплексной плоскости z определена комплекснозначная функция W=f(z)





Комплекснозначную функцию комплексного переменного можно рассматривать как пару действительных функций двух действительных переменных.
Все свойства функций действительных переменных переносятся на функции комплексного переменного.
Предел функции.
Пусть
точка
 является
предельной точкой множестваE,
то есть любая окрестность точки
является
предельной точкой множестваE,
то есть любая окрестность точки
 содержит бесконечное число точек
множестваE.
содержит бесконечное число точек
множестваE.
Число
A
называется пределом
 при
при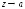 ,
если
,
если



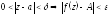
 или
или
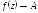 при
при
 Если
Если


 сходится кA,
т.е.
сходится кA,
т.е.

Существование

 ,
где
,
где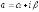 ,
равносильно существованию пределов
,
равносильно существованию пределов и
и

Пределы функции комплексного переменного обладают такими же свойствами.
Если
 ,
, ,
то
,
то


 ,
,

Непрерывность.
Пусть
 определена на множествеE
и точка
определена на множествеE
и точка
 .
.
Функция
 называется непрерывной в точке
называется непрерывной в точке ,
если
,
если





Функция
 называется непрерывной в точке
называется непрерывной в точке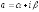 ,
если
,
если и
и непрерывны в точке
непрерывны в точке .
.
 называется
непрерывной на множестве E,
если она непрерывна в каждой точке этого
множества.
называется
непрерывной на множестве E,
если она непрерывна в каждой точке этого
множества.
Сумма, разность, произведение и частное (в тех точках, в которых знаменатель не равен нулю) непрерывных функций комплексного переменного является непрерывной функцией.
3. Дифференцирование функций. Условие Коши-Римана.
Пусть
 определена в некоторой окрестности
точки
определена в некоторой окрестности
точки .
.
Если
существует конечный предел
 (1),
(1),
то
этот предел называется производной
функции
 в точке
в точке ,
а
,
а называется дифференцируемой в точке
называется дифференцируемой в точке .
.
 называется
дифференцируемой в области, если она
дифференцируема в каждой точке этой
области.
называется
дифференцируемой в области, если она
дифференцируема в каждой точке этой
области.
 (2)
(2)

 :
:

 ,
где
,
где

Если
 (3),
то
(3),
то ,
гдеA
– комплексная постоянная, не зависящая
от
,
гдеA
– комплексная постоянная, не зависящая
от
 .
.
Равенство
(3) является необходимым и достаточным
условием дифференцируемости
 в точке
в точке .
.
Из (3)
следует, что функция, дифференцируемая
в точке
 ,
непрерывна в этой точке.
,
непрерывна в этой точке.
Пример
 C =
Const
C =
Const





Если
существует
 ,
то
,
то имеет один и тот же предел при
имеет один и тот же предел при по любому пути.
по любому пути.
Функция комплексного переменного, дифференцируемая в области, обладает производными всех порядков в этой области.
На функции комплексного переменного распространяются известные формулы дифференцирования.
Если
 и
и дифференцируемы в точкеz,
то их сумма, произведение и частное так
же дифференцируемы в этой точке.
дифференцируемы в точкеz,
то их сумма, произведение и частное так
же дифференцируемы в этой точке.
1.

2.
 ,C
= Const
,C
= Const
3.

4.

Если
 дифференцируема в точкеz,
а
дифференцируема в точкеz,
а
 дифференцируема в точке
дифференцируема в точке ,
то
,
то

Замечание.
Непрерывность
функции комплексного переменного
 в точке
в точке равносильно непрерывности функций
равносильно непрерывности функций и
и в точке
в точке .
Аналогичное утверждение не имеет места
для дифференцируемости. Именно требование
дифференцируемости функции
.
Аналогичное утверждение не имеет места
для дифференцируемости. Именно требование
дифференцируемости функции налагает дополнительные условия на
частные производные функций
налагает дополнительные условия на
частные производные функций и
и .
.
Условие Коши-Римана.
Теорема 1.
Чтобы
функция
 была дифференцируема в точке
была дифференцируема в точке необходимо и достаточно, чтобы 1) функции
необходимо и достаточно, чтобы 1) функции и
и были дифференцируемы в точке
были дифференцируемы в точке ,
и 2) в точке
,
и 2) в точке выполнялись условия Коши-Римана
выполнялись условия Коши-Римана
![]() (4)
(4)
Для
выполнения условий теоремы имеет место
формула
 (5)
(5)
Доказательство:
Необходимость.
Пусть
функция
 дифференцируема в точке
дифференцируема в точке ,
тогда
,
тогда (6)
(6)



 (7)
(7)
Выделяя в последнем выражении действительные и мнимые части находим
 (8)
(8)
Действительная
функция
 дифференцируема в точке
дифференцируема в точке только если и приращение представляется
в виде
только если и приращение представляется
в виде ,
где
,
где и
и - действительные числа, не зависящие от
- действительные числа, не зависящие от и
и .
.

При
этом
 и
и
 (9)
(9)




Аналогично
найдём, что
 .
.
Вывод:
 и
и в формулах (8) удовлетворяют условиям
(9) и поэтому функции
в формулах (8) удовлетворяют условиям
(9) и поэтому функции и
и дифференцируемы в точке
дифференцируемы в точке .
.
Из
формулы (8)
 ;
; ;
;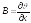 ;
;
Отсюда
следует формула Коши-Римана


Достаточность.
Пусть
функции
 и
и дифференцируемы в точке
дифференцируемы в точке и пусть выполняются условия (4), тогда
имеет место равенство (8) где
и пусть выполняются условия (4), тогда
имеет место равенство (8) где и
и .
.
Умножая
вторые из этих равенств на
 и складывая с первым получаем
и складывая с первым получаем
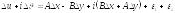 или
или
 или
или
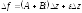 ,
где
,
где


Отсюда
следует дифференцируемость функции
 в точке
в точке .
.
Пример.



 ;
;

Функции
 ,
, ,
, z,
z,
 z
дифференцируемы во всей комплексной
плоскости и их производные вычисляются
по формулам
z
дифференцируемы во всей комплексной
плоскости и их производные вычисляются
по формулам
 ,
, ,
, ,
, .
.
Замечание.
Пусть
 ,
тогда
,
тогда


Эти формулы связывают декартовые и полярные координаты
 ;
;

Формулы для производной

