2. Однородные уравнения

Функция называется однородной функцией степениn, где n-целое, если при любом имеет место тождество

Частный случай

Дифференциальное уравнение вида называется однородным, еслии- однородные функции одинаковой степени.

Уравнение (1) может быть приведено к виду

; ;

Пример 1

Пример 2

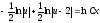
Замечание:

Уравнение вида может быть приведено к однородному посредством замены

Пример 3

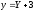
Лекция 11

Пример 4

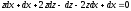
3. Линейные уравнения и уравнения Бернулли

1. Линейные уравнения.

Метод Бернулли

Пример 1

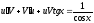
Ответ:

Пример 2

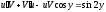
Пример 3

2. Уравнения Бернулли

Уравнение вида

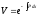
Пример 1

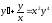
Пример 2

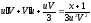
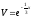
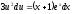
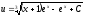
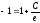
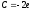
4. Уравнения в полных дифференциалах. Интегрирующий множитель.

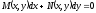(1)

(1)– уравнение в полных дифференциалах, если

Теорема

Чтобы уравнение (1) являлось уравнением в полных дифференциалах необходимо и достаточно, чтобы в некоторой области D изменение x и y выполнялось условие (2)

(2)

Общий интеграл уравнения (1) имеет вид

Пример 1

Дифференцируем по y и приравниваем N

Интегрирующий множитель.

В некоторых случаях, когда уравнение (1) не является уравнением в полных дифференциалах, удается подобрать функцию , такую что

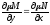
1.

2.

1.

Для существования интеграла множитель не зависит от y необходимо и достаточно, чтобы правая часть была функцией от x

Пример 2

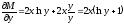
Пример 3

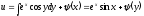
5. Интегрирование дифференциальных уравнений высших порядков.

(1)

(2)

Уравнение (1) связывающее между собой независимые переменные, неизвестную функцию , а также первые производные называют дифференциальным уравнением второго порядка.

Уравнение также может быть записано в виде (2).

Задача отыскания решения уравнения (2) удовлетворительна заданным начальным условиям называется задачей Коши.

Решением уравнения (2) называется всякая функция которая при подстановке вместеиобращает его в тождество.

Графиком функции называется функция, зависящая от двух произвольных постоянныхии такая что она является решением этого уравнения при любых конкретных значенияхипри любых допустимых начальных условиях.

Можно подобрать такие значения ичто данная функцияy будет удовлетворять заданным начальным условиям.

Теорема существования и единственности решения.

Если функция и ее частные производные,непрерывны в некоторой областиD, содержащей точку то существует единственное решениеуравнения (2) удовлетворительное начальным условиям.

Общий интеграл или общее решениепредставляет собой семейство кривых, зависящее от произвольных постоянныхи.

Задача Коши состоит в определении интегралов кривой , проходящей через данную точкуи имеющей угловой коэффициентк касательнойt (данное направление к данной точке).

Понижение порядка дифференциальных уравнений.

1). Если уравнение задано в виде , то

Пример

2). Если уравнение задано в виде или, то

Пример 1

Пример 2

3). Если уравнение задано в виде , то

Пример 1

Пример 2

Интегрирование дифференциального уравнения порядка выше второго

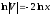
Линейные дифференциальные уравнения высшего порядка

Линейное неоднородное дифференциальное уравнение второго порядка имеет вид:

(1)

Здесь и- непрерывные функции на. При этих условиях единственное решение уравнения (1) ,удовлетворяет начальным условиям,где

Функция ‑ правая часть уравнения (1)

Если приходим к линейному уравнению второго порядка или к уравнению без правой части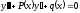 (2)

Здесь иназываются линейно-независимыми на, если

Это тождество имеет место только тогда, когда иравны 0.

Если существуют такие числа и,из которых хоты бы одно отлично от нуля, то для всехиназываются линейно-независимыми на

и называются линейно-независимыми (зависимыми) на, когда

Определитель Вронского

вронскиан

Теорема 1

Если илинейно-зависимые на, то

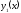Если илинейно-независимые на, то

Теорема 3

Общее решение уравнения (2) имеет вид

и -линейно-независимое решение этого уравнения.

Чтобы получить общее решение уравнения (2) достаточно найти два линейно-независимых частных решения этого уравнения. Они образуют фундаментальную систему решения уравнения (2)

Оба решения илинейно независимы

Теорема

Общее решение у линейного неоднородного дифференциального уравнения (1) представляется в виде суммы , где- общее решение соответствующего однородного уравнения (2),- некоторое частное решение уравнения (1)

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

(1)

Сводится к уравнению , которое называется характеристическим уравнением (1)

Терема 1

Пусть и- корни характеристического уравнения (2), тогда общее решение находится по одной из следующих трех формул:

1. Корни уравнения действительные и различные _=>

2. _=>

3. Корни комплексные

_=>

₄. _=>

Пример 1

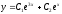
Пример 2

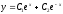
Пример 3

Пример 4

Пример 5

Пример 6

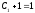
Решение однородных уравнений второго порядка

Метод Лагранжа

Пример 1

Понижение порядка

(1)

Порядок уравнения (1) можно понизить на 1 полагая, что , затем делаем замену.

Если известно k частных линейных независимых решений уравнения (1) , то порядок уравнения может быть понижен на k единиц.

(2)

Общее решение уравнения (2) есть сумма общего решения уравнения (1) и частного решения уравнения (2)

Если имеется фундаментальная система соответствующего уравнения (1),то общее решение уравнения (2) может быть найдено методом вариации произвольной постоянной или методом Лагранжа.

Общее решение уравнения (1) , где‑ произвольные постоянные.

Будем искать решение уравнения (2) в виде

(3)

где - некоторые пока независимые функции отx.

Для их определения составим систему

(4)

Решая систему уравнений (4) относительно

- произвольные постоянные

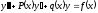
(5)

, - производные постоянные интегрирования

Пример 1

Пример 2

Пример 3