4 Сопряжённые гармонические функции

Пусть дифференцируема в областии пустьиимеют непрерывные частные производные до второго порядка включительно. Тогда

(10)

Складывая эти равенства получаем

Аналогично

Действительная функция имеющая в областинепрерывные частные производные второго порядка и удовлетворяет уравнениям (10) называется гармонической на области. А сами уравнения (10) называются уравнениями Лапласа.

Теорема.

Для дифференцируемой функции в областинеобходимо и достаточно, чтобыибыли сопряжёнными гармоническими в этой области, т.е. зная одну из функций,можно в односвязной области найти другую функцию.

Пример.

Найти дифференцируемую функцию , если.

;

Данная функция дифференцируема во всей комплексной области.

5 Конформное отображение

Пусть функция дифференцируема в некоторой точкеи

Пусть дифференцируема в некоторой окрестности точкии.

Рассмотрим гладкую кривую .

,

,

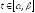
- угол, образуемый касательной к кривой в точке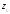и положительным направлением действительной оси в плоскости.

- образ кривой при отображении.

- образ точки .

По правилу дифференцирования сложной функции

(1)

Т.к. , то, т.е. криваяимеет касательную в точке.

Пусть , тогда, т.е.(2)

Величина называется углом поворотав точкепри отображении.

Из (1) и (2) следует если , то угол поворота в точкене зависит от вида и направления кривой и равен, т.е. все кривые, проходящие через точкуповорачиваются при отображении,на один и тот же угол, равный аргументу производной в точке.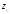

Т.о. отображение , гдедифференцируемая в окрестности точкифункция,сохраняет углы между кривыми, проходящими черезне только по величине, но и по направлению отсчёта.

6 Постоянство растяжений

Пусть дифференцируема в некоторой окрестности точкии. Рассмотрим произвольную точкукривой, расположенную достаточно близко к.

Из определения производной следует

, где при

(3)

Пусть , где- фиксировано.

Окружность переходит при отображениив кривую, которая мало отличается от окружности.

Отображение с точностью до малых более высокого порядка, чем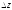растягивает кругвраз. Величинаназывается линейным растяжением кривойв точкепри отображении.

Вывод:

Линейное растяжение в точке не зависит от вида и направления кривой и равно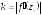. Отображениеназывается конформным в точкеесли оно сохраняет углы между кривыми и обладает свойством постоянства растяжений в точке.

Замечание:

Условие означает, что екобеан отображенияв точкеотличен от нуля.

Отображение эквивалентно действительному отображению

(4)

Если , то

7 Интеграл по комплексному переменному

Кривая (линия Жордана) называется гладкой, если она имеет непрерывно изменяющуюся касательную. Кривая называется кусочногладкой, если она состоит из конечного числа гладких дуг.непрерывна в некоторой области.- произвольная гладкая кривая, лежащая в области. Рассмотрим дугу кривой с началом в точкеи с концом в точке. Разделим эту дугу начастей произвольными точкамирасположенных последовательно и составляющих их сумму

;

Пусть - наибольшая из величин.

Если , тои суммастремится к некоторому пределу (интегралу)

Если 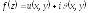, тосводится к двум криволинейным интегралам от действительных функций

Пусть - кусочногладкая линия, состоящая из гладких частей, тогда интеграл по этой линии

Теорема Коши для случая непрерывной производной.

Пусть дифференцируема в конечной односвязной областиинепрерывна в области, тогдапо любой замкнутой кривойлежащей в областиравен нулю.

Замечание и дополнение к теореме Коши.

Следствие 1.

Если дифференцируема в конечной односвязной области, тоне зависит от пути интегрирования. Кривуюможно деформировать в области, оставляя концы неподвижными и не меняя значения интеграла.

Пусть граница многосвязной областисостоит из замкнутой кусочногладкой кривойи попарно непересекаемых замкнутых кусочногладких кривыхрасположенных внутри

, где кривые ориентированы так, что при обходе каждой из них область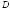остаётся слева (положительное направление обхода границы области).

Интеграл и первообразная

Если не зависит от пути интегрирования, то, где- начальная точка, а- конечная точка кривой.

Пусть фиксирована, тогда интеграл является функцией от.

Теорема.

Пусть непрерывна в конечной областии пустьпо любой замкнутой кривой лежащей в областиравен нулю, тогда, где,

Теорема.

Если дифференцируема в конечной односвязной области, то она имеет в этой области первообразную.

Теорема.

Совокупность всех первообразных функций в областиопределяется формулой, где- какая-нибудь первообразная функции, а- произвольная постоянная.

Опираясь на данные теоремы мы можем использовать формулу Ньютона-Лейбница

При удовлетворении данных теорем справедливы формулы интегрирования по частям