Содержание Двойной и тройной интегралы.

1 Двойной интеграл. Объем цилиндрического тела.

Цилиндрическим телом называется тело, ограниченное плоскостью OXY, поверхностью, с которой любая прямая, параллельная OZ, пересекается не более чем в одной точке и цилиндрической поверхностью, образующие которой параллельны OZ.

Область D, высекаемая в плоскости OXY цилиндрической поверхностью называется основанием цилиндрического тела.

В частных случаях боковая цилиндрическая поверхность может и отсутствовать (). Обычно тело можно составить из некоторого числа цилиндрических тел, и искомый объем определить как сумму объемов цилиндрических тел, составляющих это тело.

Два принципа, на которые следует обращать внимание при вычислении объема.

1. Если разбить тело на части, то его объем будет равен сумме объемов всех частей.

2. Объем цилиндрического тела, ограниченного плоскостью, параллельной OXY, равен площади основания, умноженной на высоту тела.

Пусть z=f(x, y) – уравнение поверхности, ограничивающей цилиндрическое тело. Будем считать f(x, y) непрерывной на области D. Предположим, что поверхность целиком лежит над OXY (f(x, y) > 0 в области D). V – объем цилиндрического тела.

Разобьем D на некоторое число n областей произвольной формы, будем называть их частичными областями.

Пронумеруем частичные области 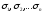, а их площади.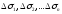

Через границу каждой частичной области проведем цилиндрическую поверхность. Таким образом, цилиндрическое тело окажется разбитым на n частичных цилиндрических тел. Заменим частичное цилиндрическое тело прямым цилиндром с тем же основанием и высотой. 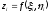Получимn-ступенчатое тело.

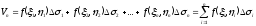
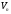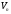Принимая объем V данного цилиндрического тела приближенно равным , будем считать, чтотем точнее выражаетV, чем больше n и чем меньше каждая из частичных областей. Переходя к пределу при 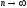будем требовать, чтобы не только площадь каждой частичной области стремилась к нулю, но и стремление к нулю всех ее размеров. Если назвать диаметром частичной области наибольшее расстояние между ее точками, то диаметры каждой из частичных областей должны стремиться к нулю. При этом сами области будут стягиваться в точку.

Мы принимаем объем V при стремлении к нулю наибольшего диаметра частичных областей. Эта сумма называется n-ой интегральной суммой для f(x, y) в области D соответствующей разбиению на n частей.

Опр. Предел, к которому стремится n-ая интегральная сумма при 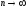и при стремлении к нулю наибольшего диаметра частичной области, называется двойным интегралом функцииf(x, y) по области D.

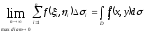
Теорема о существовании.

n-ая интегральная сумма, соответствующая конечной области D и непрерывной в этой области f(x, y) стремится к пределу при 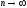и при стремлении к нулю наибольшего диаметра частичных областей. Этот предел не зависит ни от способа подразделения областиD на частичные, ни от того, какие точки в частичных областях выбираются в качестве .

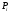2 Свойства двойных интегралов

1) Линейность

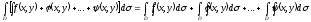
2) Постоянный множитель можно вынести за знак двойного интеграла

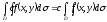
3) Аддитивность

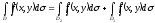
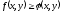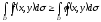4) Если во всех точках D , то. Если подынтегральная функция в области интегрирования не меняет знак, то двойной интеграл есть число того же знака, что и функция. Если в двойном интеграле подынтегральная функция тождественно равна 1, то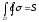. Двойной интеграл выражает объем прямого цилиндра с высотой 1, т. е. численно равен площади основания цилиндра.

5) Если 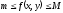, то, гдеS-площадь области D

6) Двойной интеграл равен произведению значения подынтегральной функции в некоторой точке области на площадь области интегрирования 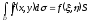.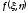- среднее значение функцииf(x, y) в области D.

Геометрический смысл теоремы о среднем.

Существует цилиндр, основание которого совпадает с основанием D, высота равна аппликате поверхности в некоторой точке основания, а объем равен объему цилиндрического тела. Указанная аппликата изображает среднее значение на области D.