2 Вычисление криволинейного интеграла по координатам

Разделим дугу наточками.

Теорема о существовании криволинейного интеграла второго рода.

Если инепрерывны и имеют непрерывные производные, а так же непрерывны функцииипри

Существуют

и ‑ координаты некоторой точки, лежащей на дуге

Эти пределы не зависят ни от способа деления L на при условии, что, ни от выбора точки

Замечание:

Из теоремы следует, если у нас имеется трехмерное пространство

Существование по замкнутому контуру не зависит от выбора точки начала интегрирования.

Пример 1

Вычислить

Пример 2

3 Криволинейный интеграл первого рода (по длине дуги)

Интегральной суммой для функции по длине дугиAB называется сумма вида

Криволинейным интегралом по длине дуги AB от называется предел интегральной суммы при

Если кривая L задана параметрическими уравнениями

Аналогично вычисление криволинейного интеграла первого рода от функции 3-х переменных

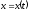
Физический смысл

Если , топредставляет собой массу кривойL, имеющей переменную линейную плотность

Если , точисленно равен площади цилиндрической поверхности, у которой направляющаяL лежит в плоскости OXY, а образующие перпендикулярны ей. Эта цилиндрическая поверхность ограничена сверху поверхностью

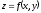
4 Основные свойства криволинейного интеграла первого рода

1). Криволинейный интеграл первого рода не зависит от направления пути интегрирования

=

2).

3).

4). Если контур интегрирования разбить на 2 части и

Пример 1

L: A(0,0) B(4,3)

Пример 2

L: O(0,0) A(1,2)

5. Формула Грина.

Установим связь между двойным интегралом по некоторой плоскости области D и кривым интегралом по границе L этой области.

Пусть в OXY задана правильная область D (как в направлении Ox, так и в направлении Oy)

В совокупности обе эти кривые составляют замкнутую область D.

Пусть в этой области иимеют непрерывные частные производные.

Рассмотрим (1)

(2)

Аналогично (3)

(2),(3) (1)

(4)

Сумма кривых интегралов, стоящих в правой части равна кривому интегралалу по всей кривой L взятому по часовой стрелке

(5)

Если часть границы составляет отрезок Oy, то интеграл по нему равен нулю.

(6)

Вычитая (5)-(6)

Если обход контура L совершается против часовой стрелки

Условие независимости криволинейного интеграла от пути интегрирования.

взятый по некоторой плоской кривой L, соединяет точки M и N

Будем полагать, что ибудут иметь непрерывные частные производные

Рассмотрим две произвольные кривые MPN и MQN

(1)

- интеграл

Взят по замкнутому контуру L, состав из MPN и NQM

Вывод:

Из условия что M и N кривой интеграл не зависит от соединения их кривой, а зависит только от положения этих точек.

Справедливо и обратное утверждение. Если криволинейный интеграл по любому замкнутому контуру равен нулю, то он не зависит от формы кривой, а зависит только от положения этих точек.

Теорема.

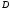
Пусть во всех точках ,вместе со своими частными производными непрерывны. Чтобы криволинейный интеграл был равен нулю, необходимо и достаточно, чтобы(3)(2)

Доказательство:

Рассмотрим произвольный замкнутый контур в области.

Если выполнено условие (3), то двойной интеграл стоящий слева тождественно равен нулю, следовательно .

Необходимость.

Допустим, что (2) выполняется, а (3) не выполняется хотя бы в одной точке .

потому что в левой части неравенства стоит положительная функция

Но по формуле Грина левая часть последовательного неравенства равна криволинейному интегралу по границе области, который по предположению равен нулю.

Вывод: последнее неравенство противоречит условию (2), значит предположение, что отлично от нуля хотя бы в одной точке неверново всех точках данной области.

- полный дифференциал.

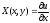
- потенциал вектора.

Теорема.

Криволинейный интеграл по любой соединяющей точкииравняется разности значений функциив этих точках

Для вычисления этого интеграла напишем параметрическое уравнение кривой 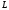соединяющей точк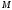ии.

Будем считать, что значение соответствует точке, а значениеточке, тогда криволинейный интеграл сведётся к следующему определённому интегралу.

Выражение в квадратных скобках есть выражение полной производной функции

Криволинейный интеграл не зависит от формы кривой. Это справедливо и для криволинейного интеграла по пространственной кривой.

Замечание.

Иногда приходится рассматривать криволинейный интеграл по длине .

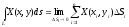(4)

- дифференциал дуги.

Вычисление таких интегралов аналогично вычислению, рассмотренному для криволинейных интегралов.

:

- непрерывные функции.

Т.к.

Можно рассматривать криволинейный интеграл по дуге пространственной кривой

С помощью криволинейного интеграла по дуге определяем координаты центра тяжести линии