
tot_book
.pdf181
вначале кривые ln ϑ1 = f (τ) и ln ϑ2 = f (τ) будут иметь различный характер, а начиная с некоторого τ станут параллельными прямыми.
Таким образом, можно выделить две стадии процесса — начальную и регулярную; в последней избыточная температура во всех точках тела меняется во времени экспоненциально: поскольку
ln ϑ = −mτ+C, |
(2.93) |
ϑ = Ce−mτ. |
(2.94) |
Величина m > 0 не зависит от координат и времени; она характеризует интенсивность отвода или подвода теплоты, называется темпом охлаждения (или темпом нагрева) и входит в экспоненциальную функцию (2.94) в виде множителя при времени
τ.
Для двух произвольных моментов τ' и τ" > τ' по формуле
(2.93) определим |
|
|
|
|
|
|
|
|
m = |
ln ϑ′−ln ϑ′′ |
, |
(2.95) |
|
|
|
τ′′−τ′ |
||||
|
|
|
|
|
|
|
′ ′′ |
|
|
|
|
|
|
где ϑ ,ϑ — значения ϑ, соответствующие моментам τ' и τ". |
|
|||||
Итак, |
если |
представить |
кривую |
охлаждения |
в |
|
полулогарифмических координатах, то, начиная с некоторого момента, она превратится в наклонную прямую, а темп охлаждения тела будет угловым коэффициентом этой прямой: m = tgϕ.
Используя понятие темпа охлаждения m, Г.М. Кондратьев сформулировал две теоремы.
Первая теорема Кондратьева: темп охлаждения однородного тела при конечном значении коэффициента теплоотдачи α прямо пропорционален α и поверхности тела F и обратно пропорционален полной теплоемкости тела сρV:
m = ψ |
αF |
. |
(2.96) |
|
|||
|
cρV |
|
|

|
|
|
182 |
|
|
|
|
||||||
|
|
Множитель |
ψ = ϑF ϑV |
называют |
|
коэффициентом |
|||||||
неравномерности распределения температуры ( |
|
F — среднее по |
|||||||||||
ϑ |
|||||||||||||
поверхности тела F значение ϑ, |
|
V |
— то же значение, усредненное |
||||||||||
ϑ |
|||||||||||||
по объему V). |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
При Вi→0 температура в теле распределяется почти |
|||||||||||
равномерно, поэтому |
|
F ≈ |
|
V , ψ =1. При |
Вi→∞, наоборот, |
||||||||
ϑ |
ϑ |
||||||||||||
|
|
F → 0, поскольку Тw→Tf, поэтому |
ψ = 0. Следовательно, во всех |
||||||||||
|
ϑ |
||||||||||||
случаях 0 ≤ ψ ≤1. |
|
|
|
|
|
|
|
|
|
|
|
||
Вторая теорема Кондратьева: при Вi→∞ (или, что то же,
при α→∞) темп охлаждения m∞ прямо пропорционален
температуропроводности тела: |
|
a = Km∞, |
(2.97) |
где К — коэффициент, зависящий только от формы и размеров тела, его размерность — м2.
Например, |
для |
пластины |
|
толщиной 2δ при Вi→∞ и для |
|||||||||||||||
Fо>>0,3 e−µ12Fo = e−m∞τ, откуда |
|
µ |
≈ π |
|
Fo = |
aτ |
: |
||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
δ2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
µ2a |
|
|
π2a |
|
|
π 2 |
|
|
|
|
|
||||
|
m |
= |
1 |
= |
4δ2 |
= |
|
|
|
a . |
|||||||||
|
|
||||||||||||||||||
|
∞ |
|
δ2 |
|
|
|
|
2δ |
|
|
|
|
|
||||||
Поэтому |
K = |
|
1 |
|
|
— коэффициент пропорциональности |
|||||||||||||
(π 2δ)2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
для регулярного нагрева (охлаждения) пластины. |
|||||||||||||||||||
Показано, что для шара радиусом r0 |
|
|
|
|
|
||||||||||||||
|
|
|
|
K |
= |
1 |
|
|
; |
|
|
|
|
|
|
|
|||
|
|
|
|
(π r |
)2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
для параллелепипеда размерами l1 × l 2 × l 3 |
|||||||||||||||||||
|
K = |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
; |
|
|
||
|
(π l )2 |
+ |
(π l |
2 |
)2 +(π l |
|
)2 |
|
|
||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
3 |
|
|
|
|
||||
для цилиндра радиусом r0 и длиной l

|
|
|
183 |
|
|
|
K = |
|
|
1 |
|
|
. |
|
2,405 |
2 |
|
π 2 |
||
|
|
r |
|
+ |
|
|
|
|
|
l |
|||
|
|
0 |
|
|
|
|
Соотношения (2.96) и (2.97) можно объединить, если ввести обозначения:
M = m = mK — относительный темп охлаждения, m∞ a
B = αλ K VF — модифицированное число Био
(в этих обозначениях М = ψВ).
Мы уже убедились, что коэффициент ψ определяется числом Био; эксперимент показывает, что для тел произвольной формы
ψ (1+1,44B + B2 )−1 2. |
(2.98) |
Формула (2.98) содержит оценку неравномерности регулярного поля температуры в любом теле, если для него известны величины λ, a, α, К, F и V.
Пользуясь теорией регулярного теплового режима, можно определить теплофизические свойства материала, образующего однородное тело. Если жидкость интенсивно перемешивать (α→∞), то по формуле (2.97) удается определить a. Если на границе тела поддерживать постоянное и конечное значение αа, то сначала можно определить µ1(Вi), а затем и величину λ. В обоих случаях кривые охлаждения представляют в полулогарифмических координатах.
Выше речь шла о нагреве и охлаждении тел в среде с Тf=const при Fо >> 0,3; такой процесс называют регулярным режимом первого рода. Если температура среды меняется во времени
линейно (Тf = Тf0 + ωτ) или гармонически (Тf = Тf0 + Тm соsπωτ), то говорят о регулярном режиме соответственно второго или третьего рода (здесь ω, Тf0, Тm — константы).
В 1967 г. А.В. Лыков показал, что все разновидности регулярного режима характеризует одна особенность: скорость

184
нагрева тела прямо пропорциональна разности температуры среды Тf и среднемассовой температуры тела T :
|
|
|
|
|
|
|
− |
∂T |
= m(Tf −T |
). |
(2.99) |
||
∂τ |
||||||
|
|
|
|
|||
Важно помнить, что в формуле (2.99) темп m зависит не только от размеров, теплофизических свойств и граничных условий, но и от того, как меняется температура среды Тf.
Метод регулярного теплового режима использует простой математический аппарат и удобен как в эксперименте, так и при расчете процессов нестационарной теплопроводности.
2.5. ПРИБЛИЖЕННЫЕ МЕТОДЫ ТЕОРИИ ТЕПЛОПРОВОДНОСТИ
Чаще всего расчеты теплопроводности начинают с оценки стационарного поля температуры (если оно существует) и с определения тепловых потоков.
Если тепловые процессы зависят от времени, переходят к расчету нестационарной теплопроводности, рассматривая стационарные решения как предельные. В обоих случаях используют упрощенные модели тел (пластину, цилиндр, шар, стержень). Важно помнить, что аналитических решений задачи Фурье чрезвычайно много, но большинство из них громоздки, требуют квалифицированного анализа, да и воспользоваться справочной литературой удается далеко не всегда.
Можно, конечно, провести детальное аналитическое решение краевой задачи или поставить специальный эксперимент — если для этого есть время, средства и квалификация! Но нельзя забывать, что расчетная модель может оказаться слишком грубой, а теплофизические свойства материалов редко известны с точностью, превышающей 10…20 %. Поэтому нельзя переоценивать и точность полученных результатов; их необходимо обязательно проверить в предельных случаях (на поверхности тела, при τ→∞, α→∞ и т. д.), сопоставить с результатами испытаний,
185
наблюдениями, словом, не следует терять здравого смысла. Кроме того, полезно вспомнить о приближенных (инженерных) методах расчета, дающих приемлемую для практики точность.
2.5.1. Электротепловая аналогия
При расчете стационарной теплопроводности пластин и оболочек мы ввели понятие термических сопротивлений — внутреннего Rλ, внешнего Rα и полного Rk. Термин “сопротивление” выбран не случайно, поскольку уравнение, описывающее поле температуры в сечении пластины, совпадает по структуре с законом Ома для участка цепи постоянного тока. На рис. 80 показана так называемая тепловая цепь сопротивлений — аналог электрической цепи.
Кроме перечисленных выше термических сопротивлений Rλ,
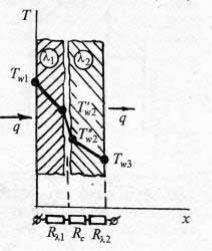
Rα, Rk, в расчет иногда вводят контактное термическое сопротивление Rtc; его смысл поясняет рис. 98. Если две пластины не находятся в идеальном тепловом контакте (из-за шероховатости, присутствия
Рис. 98.
загрязнений, смазки и т. п.), то на границе возникает скачок температуры ∆Ttc =Tw′2 −Tw′′2. Поскольку в стационарной задаче
186
теплопроводности для пластины |
в любом поперечном |
сечении |
||||
q = idem, контактное термическое сопротивление |
|
|||||
R |
= ∆Ttc = |
Tw′2 −Tw′′2 |
. |
(2.100) |
||
|
||||||
tc |
q |
q |
|
|||
|
|
|
||||
Итак, контактное термическое сопротивление численно равно отношению разности температур на границе соприкосновения двух шероховатых тел к плотности теплового потока на этой границе.
Простота формулы (2.100) обманчива, поскольку величину ∆Ttc измерить и тем более рассчитать весьма сложно. Обычно значение Rtc задают по опытным данным, а в первом приближении принимают равным нулю.
Формальное сходство уравнений тепло- и электропроводности получило название электротепловой аналогии (ЭТА). Метод ЭТА позволяет рассматривать систему тел,
вкоторой идут процессы теплопроводности, как тепловую цепь, диалогичную цепи электрической. Обычно тепловые цепи начинаются и заканчиваются в точках, имеющих постоянную температуру — аналог постоянного потенциала в электрической цепи.
Метод ЭТА кажется весьма простым, но в нем есть существенная особенность, о которой следует помнить. Если результаты расчета электрических цепей весьма точно соответствуют эксперименту, то это связано в первую очередь с тем, что удельные электрические сопротивления проводников и изоляторов отличаются на много порядков. Теплопроводность различных материалов таким свойством не обладает; она меняется
впределах 0,01…400 Вт/(м·К), а для твердых материалов диапазон
изменений λ еще меньше. Во всех задачах, кроме явно одномерных (см. рис. 77–84 и т. п.), приходится вводить дополнительное допущение — гипотезу адиабатности или гипотезу изотермичности.
187
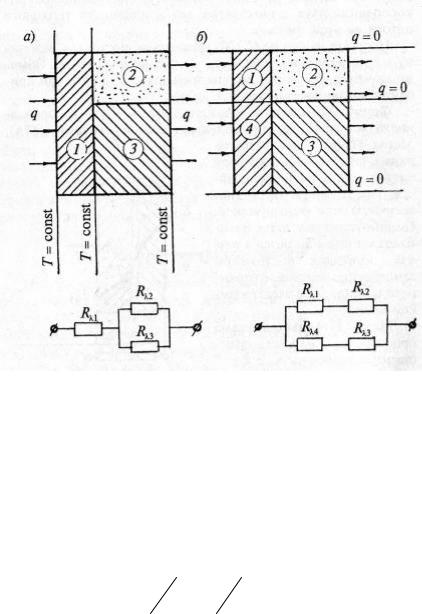
Рис. 99.
Если пластину мысленно “разбить” изотермами Т = const (рис. 99,a), то тепловую цепь составят три внутренних сопротивления, а при “разбиении” сечениями q = 0 (рис. 99,б) — четыре; результаты расчета суммарных сопротивлений при этом будут такими:
RλΣ |
|
T =const |
= Rλ1 + |
|
|
1 |
|
; |
|
|||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||
|
|
1R |
+ 1R |
|
||||||||
|
|
|
|
|
|
|
λ2 |
λ3 |
|
|||
|
|
|
|
|
1 |
|
|
1 |
|
−1 |
||
|
|
|
|
|
|
|
||||||
RλΣ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
q=const |
= R |
+ R |
+ R |
+ R |
. |
||||||
|
||||||||||||
|
|
|
λ1 |
|
|
λ2 |
|
λ3 |
|
λ4 |
|
|
Расчеты дают близкие, но не идентичные результаты (в чем легко убедиться, задав реальные размеры и теплопроводности материалов). При построении тепловой цепи необходимо сразу же остановиться на одной из схем или при возможности рассмотреть обе. И помнить: для двумерных и трехмерных задач метод ЭТА имеет ограниченную, а иногда сомнительную точность, его следует считать лишь оценочным.
Мы подошли, по сути, к расчету составных тел: они включают области с различными теплофизическими свойствами, причем на границах областей соблюдаются условия IV рода. Это —
188
неподвижные соединения деталей, выполненные путем сварки, пайки, склейки; посадочные соединения с натягом, различные композиты (армированные пластики, железо-бетон и т. д.). Если составное тело рассматривать как единое целое, следует ввести теплопроводность λе, которую называют эквивалентной. Ее определяет соотношение
∆T |
= |
δΣ = RλΣ, |
(2.101) |
q |
|
λe |
|
где δΣ — размер (габарит) системы, для которого рассчитывается величина λе.
Поскольку RλΣ зависит от размеров, расположения и свойств элементов составного тела, общего правила для определения значения λе не существует, в каждом случае надо строить “свою” формулу (2.101), определяя конкретный вид правой части.
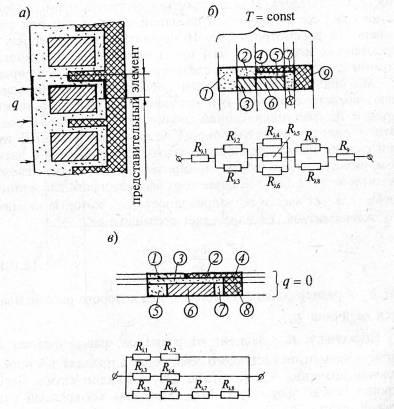
Определим, например, значение λе для сечения армированного композитного покрытия (резинометаллической гусеницы). На рис. 100 обозначим, как и прежде, цифрами элементы, для каждого из которых будем определять внутреннее термическое сопротивление Rλi (для простоты все элементы выбраны прямоугольными, а система координат — декартовой, но общность рассуждений не нарушится и для более сложных случаев). Поскольку “рисунок” сечения повторяется, а его элементы обладают зеркальной симметрией, выберем представительный элемент (рис. 100,a) и разобьем его адиабатными и изотермическими сечениями (рис. 100,б,в).
189
Рис. 100.
Как видим, тепловые схемы заметно различаются, причем расчет по схеме рис. 100,в кажется более компактным. Для него, в частности,
|
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
−1 |
|
|
|
|
|
|
|
|
|
||||||
RλΣ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
q=const |
= R |
+ R |
+ R |
+ R |
+ R |
+ R |
+ R |
+ R |
. |
||||
|
||||||||||||||
|
|
|
|
λ1 |
λ2 |
|
λ3 |
λ4 |
|
λ5 |
λ6 |
λ7 |
λ8 |
|
Метод ЭТА позволяет в общем случае решать и нестационарные задачи: для этого либо переходят к аналогии с переменным током и вводят электрические емкости, либо рассчитывают “временные” омические сопротивления и подключают их в узлы "стационарной" цепи сопротивлений (метод Дж. Либманна); оба способа громоздки, их применяют сравнительно редко. Иногда вместо расчета собирают реальные цепи электрических сопротивлений или используют электропроводную бумагу, электролиты и пр. Такой подход активно развивался до появления компьютеров, сейчас он почти вытеснен из практики, хотя иногда позволяет быстро получить нужный результат.

190
Итак, метод ЭТА наиболее полезен при расчете одномерных задач и для составных тел; в последнем случае надо помнить о его приближенном характере.
Существует, кроме того, и более общее понятие о термическом сопротивлении. Если через тело произвольной формы проходит тепловой поток Q, а разность температур (наибольшая в направлении потока) равна ∆T, то величину
R = ∆QT , К/Вт,
называют термическим сопротивлением тела.
Для стержней и цилиндров неограниченной длины рассчитывают удельную величину термического сопротивления тела на единицу длины:
R = |
∆T |
, (К м)/Вт. |
Q |
||
|
l |
|
При соблюдении граничных условий III рода (теплопередача при разности температур жидкостей Tf 1 −Tf 2 = ∆Tα ).
RΣ = ∆QTα , К/Вт.
Поскольку ∆Tα =Tf 1 −Tf 2 > ∆T =Tw1 −Tw2 , во всех случаях
RΣ > R .
Величины R , RL , RΣ многочисленных и разнообразных по форме тел сведены в таблицы; фрагмент такой таблицы представлен на рис. 101.
