
tot_book
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
171 |
|
|
|||
|
|
|
|
ϑ0 |
|
∂Θ |
= a |
ϑ |
∂2Θ |
; |
|
|||||||||
|
|
|
|
|
|
∂τ |
0 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
δ2∂L2 |
|
|
||||||||
|
|
|
|
|
∂Θ |
|
|
= |
∂2Θ |
; |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||
|
|
|
|
|
aτ |
|
|
|
|
|||||||||||
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
|
∂L |
|
|
|
|
||
|
|
|
|
δ2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
∂Θ |
|
|
∂2Θ |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
= ∂L2 . |
|
|
(2.78) |
|||||||
|
|
|
|
|
∂(Fo) |
|
|
|||||||||||||
|
Краевые условия в безразмерной форме: |
|
||||||||||||||||||
|
|
|
|
|
∂Θ |
|
|
|
|
|
= BiΘw |
|
(2.79) |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
∂L |
|
L=±1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Θ = |
Tw −Tf |
|
Θ |
|
Fo=0 =1, |
|
|
|
(2.80) |
||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||
где |
— безразмерная |
избыточная |
температура на |
|||||||||||||||||
|
||||||||||||||||||||
|
|
T −T |
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
поверхности пластины. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Искомая функция зависит всего от трех переменных: |
|||||||||||||||||||
|
|
|
|
|
Θ = Θ(Bi,Fo,L), |
|
(2.81) |
|||||||||||||
вот почему запись краевой задачи Фурье в форме (2.78)–(2.80) удобнее, чем в размерной форме (2.75)–(2.77). Кроме того, задача получает обобщение: решение (2.81) описывает поле температуры в любой пластине, независимо от численных значений α,δ, a = λ/(ρс), и в любой момент τ = Foaδ2 .
Решение (2.81) представляют собой сумму бесконечного ряда
∞ |
|
Θp = ∑An (µn )cos(µnL)e−µn2Fo , |
(2.82) |
n=1 |
|
где µn — корни характеристического уравнения |
|
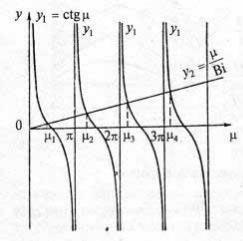
ctgµ = µ/ Bi. |
(2.83) |
172
Рис. 92.
Трансцендентное уравнение (2.83) решим графически, построив кривые y1 = ctgµ и y2 = µ/ Bi в осях у–µ (рис. 92). Из графика видно, что корней уравнения (2.83) — бесконечное множество, они приведены в виде таблиц в справочной литературе.
Функцию cos(µnL) называют собственной функцией задачи
(2.78)–(2.80).
Коэффициент разложения (амплитудная функция)
A |
(µ |
|
) = |
|
2sin µn |
|
; |
(2.84) |
|
µn +sin µn cosµn |
|||||||
n |
|
n |
|
|
|
|||
значения An (µn ) также табулированы. |
|
Пользуясь таблицами |
||||||
значений An и µn |
|
можно |
рассчитать |
|
величину Θ с любой |
|||
точностью; обычно принимают n ≤ 6, а для Fо ≥ 0,3 хватает и одного первого корня µ1:
Θ |
|
Fo≥0,3 = A1(µ1)cos(µ1L)e−µ12Fo |
(2.85) |
|
|||
|
|
Условие (2.85) соответствует так называемому регулярному тепловому режиму (см. разд. 2.45).
По мере увеличения значений Вi линия у2 на рис. 92 будет отклоняться от оси абсцисс на все меньший угол и при Вi→∞
сольется с осью µ, что даст корни |
µ = π |
, µ = |
3π |
,...,µ = |
(2n −1)π |
; |
|
|
|
||||||
|
1 |
2 |
1 |
2 |
1 |
2 |
|
|
|
|
|
|
|||
173
при этом An = (2n −1)n+1 (практически это произойдет при Вi>100).
µn
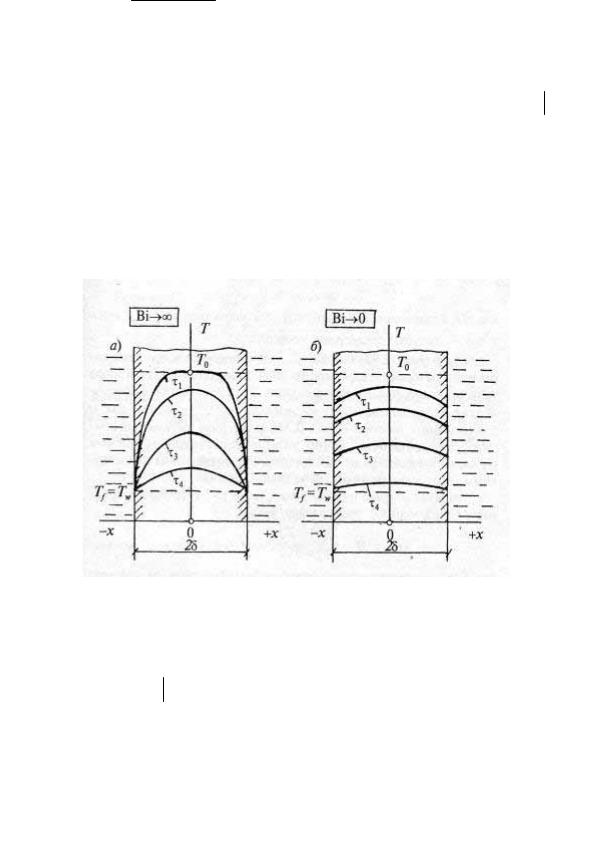
В этом случае αλ → ∞, Tw →Tf , граничные условия III рода выродятся в условия I рода. Распределение температуры T (x) Bi→∞
представлено на рис. 93,a.
Другой предельный случай — Вi→0; уравнение (2.82) при этом переходит в форму,
Θ = e−BiFo , |
(2.86) |
которая соответствует практически равномерному распределению температуры ϑ(L)L+1 (рис. 93,б). Заметим, что равенство (2.86) в
точности совпадает с соотношением (2.62), полученным в разд. 2.4.1 для термически тонких тел.
Для цилиндра и шара распределения температуры также выражаются суммами членов бесконечных рядов:
— для неограниченного цилиндра
∞ |
|
2J1(µn ) |
|
|
|
|
r |
|
2 |
|
|
Θc = ∑ |
|
|
|
|
|
|
−µnFo |
|
|
||
|
|
|
|
J0 |
µn |
|
e |
|
, |
(2.87) |
|
2 |
2 |
(µn )] |
|
|
|||||||
n=1µn [J0 |
(µn ) + J1 |
|
|
r0 |
|
|
|
||||
174
где J0(µ), J1(µ), — функции Бесселя первого рода нулевого и первого порядка, соответственно; r/r0 — безразмерная координата
для цилиндра радиусом r0 (здесь r |
≤ r0 — текущая |
размерная |
||||||
координата); |
|
|
|
|
|
|
|
|
— для шара |
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
µn |
|
|
|||
∞ |
|
|
|
|||||
2(sin µn −µn cosµn )sin |
r0 |
|
|
|||||
Θb = ∑ |
|
|
|
|
|
e−µn2Fo , |
(2.88) |
|
|
|
r |
|
|
||||
n=1 |
|
|
|
|
||||
|
|
µn |
|
|
|
|
|
|
|
r |
|
|
|
||||
|
(µn sin µn cosµn ) |
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
где r/r0 — безразмерная координата для шара радиусом r0 (здесь r ≤ r0 — текущая размерная координата).
В формулах (2.87) и (2.88) µn — корни соответствующих характеристических уравнений, их значения для цилиндра и шара табулированы, как и сами функции Θc и Θb. В обе формулы входит
экспоненциальный множитель e−µ2nFo , причем, как и для пластины, начиная с Fо ≥ 0,3 безразмерная избыточная температура достаточно точно определяется первым членом соответствующего ряда: для цилиндра и шара, как и для пластины, наступает регулярный тепловой режим.
В задачах нагрева и охлаждения часто требуется найти среднюю безразмерную температуру тела
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
T |
(τ) −Tf |
= f (Fo), |
|
|||
|
|
|
|
Θ = |
|
|||||||||
|
|
|
|
|
T |
−T |
f |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|||
где |
|
|
(τ) — среднемассовая (среднеобъемная) температура тела в |
|||||||||||
T |
||||||||||||||
момент τ. |
|
|
|
|
|
|
|
|||||||
|
|
Для тел канонической формы (пластины, цилиндра, шара) |
||||||||||||
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
= ∑Bn (µn )e−µn2Fo , |
(2.89) |
|||||||
|
|
|
|
|
Θ |
|||||||||
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
где |
|
Bn (µn ) — функции, |
вычисленные и |
табулированные для |
||||||||||
каждого из этих тел.

175
В инженерных расчетах вместо формул (2.89) можно использовать соответствующие графики; в справочной литературе они приводятся для пластин, цилиндров бесконечной длины, шаровых стенок и некоторых других тел.
При заданных Вi и Fо последовательно находят Θ, затем T (τ) = Θ(T0 −Tf )+Tf , после чего определяют количество теплоты,
отданное телом за время τ:
Qτ = cρV [T0 −T (τ)].
|
|
(τ) →Tf процесс теплопередачи закончится, |
поэтому |
|||||||||
При T |
||||||||||||
максимальное количество теплоты, отданное телом, |
|
|||||||||||
|
|
Qmax = cρV (T0 −Tf |
). |
|
(2.90) |
|||||||
Величину |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Θ (Bi,Fo)= |
T0 −T |
(τ) |
= |
|
Θτ |
|
|
|||
|
|
|
|
Θmax |
|
|||||||
|
|
|
T |
−T |
f |
|
|
|||||
0 |
|
|
|
|
τ |
|
||||||
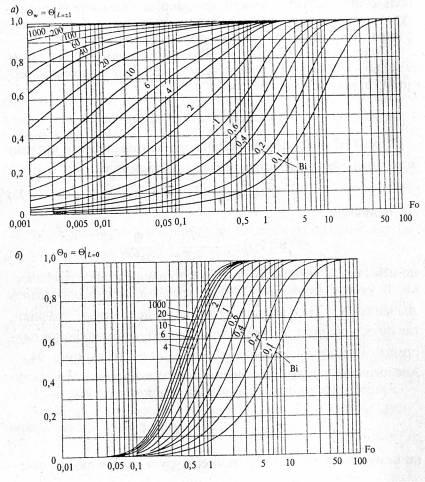
по известным значениям Вi и Fо также определяют графически. С учетом формулы (2.90) из графика можно определить значение Θτ. Для расчета температур используют графики, где по оси ординат отложена температура на поверхности пластины Θw (рис. 94,а) или в ее осевом сечении Θ0 (рис. 94,б). Аналогичные кривые построены для цилиндра и шара. Кроме того, иногда используют график (рис. 95)
Θ = T (x,τ) −Tf
T (0,τ) −Tf
по нему можно определить температуру Т(х, τ) в любом сечении
L = δx , если известна избыточная температура в средней плоскости
[T (0,τ) −Tf ]. Аналогичные графики построены для цилиндра, шара и полуограниченного тела.
176
Рис. 94.
Пользуясь перечисленными “семействами” графиков, можно решать два класса задач:
1. Определять значения температур (безразмерных и размерных) в сечении тела, если заданы его теплофизические свойства, размеры, коэффициент теплоотдачи на поверхности и текущее время:
Θ = Θ(Bi,Fo). |
(2.91) |

177
Рис. 95.
Задачу (2.91) решают непосредственно по графикам (рис. 94, 95) или по их аналогам: рассчитывают числа Вi, Fо, L, а затем определяют температуру в центре, на поверхности, в точке с координатой х или среднемассовую. Такой подход позволяет для любого заданного времени рассчитать поле температуры, например, в сечении теплоизолированного ограждения вокруг отсека при пожаре, в сечении стенки кузова после выезда автомобиля из теплого гаража и т. д.
2. Определять время, к которому температура (средняя) достигнет заданного уровня Θ:
Fo = Fo(Bi, |
|
). |
(2.92) |
Θ |
Задача (2.92) связана с выбором предельных тепловых режимов: если значение Θ ограничено теплостойкостью материалов, а также предельной допустимой температурой в отсеке или салоне транспортного средства, то число Fо определит время, в течение которого объект находится в приемлемом состоянии. Возможна и менее “тревожная” постановка задачи, когда, например, требуется определить время прогрева салона зимой или охлаждения (кондиционером или вентилятором) летом.
2.4.4. Нагрев и охлаждение тел конечных размеров
178
Тела канонической формы (пластина, цилиндр, шар) далеко не исчерпывают все практически важные для инженеровтранспортников случаи. Почти всегда тело ограничено в двух или трех направлениях, причем ясно, что поле температуры в его объеме заведомо неравномерно (Bi >> 0,1). Если по-прежнему считать, что теплофизические свойства материала (λ,ρ,с) не зависят от температуры, то температуры в двух-и трехмерных областях можно рассчитать, применяя решения, полученные для тел канонической формы.
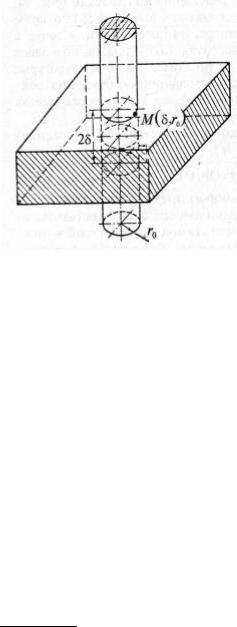
Рис. 96.
Рассмотрим в качестве примера круговой цилиндр радиусом r0 и длиной 2δ. Необходимо рассчитать температуру в точке M(δ,r0), если в начальный момент цилиндр имел температуру T0, а в момент τ = +0 на всей его поверхности начался конвективный теплообмен со средой, имеющей температуру Tf, при постоянном коэффициенте теплоотдачи а (граничные условия III рода). Представим наш “короткий” цилиндр как пересечение бесконечно длинного цилиндра радиусом r0 и неограниченной пластины толщиной 2δ (рис. 96). Для любого τ в этом случае окажется справедливой формула
ΘM = ϑMϑ(δ,r0 )= C(r0 )P(δ),
0
179
где С(r0) — значение Θc для цилиндра радиусом r0, значение Θp для пластины толщиной 2δ, ϑ0 =Tf −T0 — избыточная температура
среды; ϑM (δ,r0 ) = TM (δ,r0 ) −T0 — избыточная температура в точке
M (δ,r0 ).
Значения С(r0) и Р(δ) находят по соответствующим графикам для цилиндра и пластины. Аналогично решают задачу нагрева (охлаждения) параллелепипеда размерами 2х × 2у × 2z:
ΘM (x, y, z) = P(x), P( y), P(z),
где Р(х), Р(у), Р(z) — значения температур для пластин толщиной 2х, 2у, 2z, соответственно.
Итак, общее правило таково: безразмерная температура тела конечных размеров, образованного пересечением канонических тел, равна произведению безразмерных температур, рассчитанных для каждого из этих тел в предположении, что их поверхности пересекаются, ограничивая тело конечных размеров. Этим способом рассчитывают температуру на поверхности, в центре тела и среднемассовую температуру.
Описанный метод впервые был предложен Р. Зодербергом в 1931 г.; поскольку функции Р(х), С(r0) и т. д. входят в расчетные формулы в виде произведений, его называют
мультипликативным.
2.4.5. Регулярный тепловой режим
Эксперимент показывает, что нередко при конвективном теплообмене на поверхности тел самой различной формы (в том числе — “неправильной”, сложной) температура во всех точках тела, где бы они ни находились — на поверхности или в глубине —

180
меняется во времени по экспоненте6. Мы отмечали, что в уравнениях (2.82), (2.87), (2.88) при Fо ≥ 0,3 значения безразмерных избыточных температур Θp, Θc, Θb достаточно точно определяются одним первым членом соответствующих бесконечных рядов.
Рис. 97.
Все изложенное было хорошо известно уже в начале XX в., но лишь в 1954 г. Г.М. Кондратьев предложил весьма простую и логичную теорию теплового режима, названного регулярным. В дальнейшем в исследованиях А.В. Лыкова, Г.Н. Дульнева и др. теория регулярного режима была распространена на системы тел с внутренними источниками теплоты и прочие важные для практики случаи.
Теория регулярного режима требует, чтобы теплообмен со средой происходил при граничных условиях III рода, а тепловой поток на границе тела не менял знака (т. е. тело должно или нагреваться, или охлаждаться в течение всего процесса).
Других ограничений нет: форма тела и начальное распределение температур могут быть произвольными. Если определить (расчетно или экспериментально), как меняется температура Т в любых двух точках 1 и 2 охлаждаемого тела (рис.
97), а затем построить |
графики |
ln ϑ = f (τ), где ϑ = |
T −Tf |
, то |
6 Это означает, что в |
любой |
момент поле избыточной |
(над |
|
температурой окружающей среды) температуры остается в |
теле |
|||
“подобным самому себе”. О подобии подробнее см. в разд. 2.7. |
|
|||
