tot_book

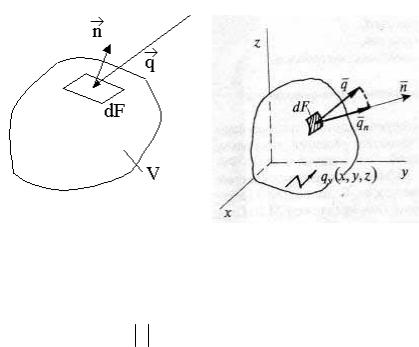
131

Рис. 73.

Вектор плотности теплового потока q на этой площадке имеет проекцию на нормаль

qn = q cos(qr,nr).

В декартовых координатах х, у, z

Теплота QF, подведенная через всю поверхность среды F за время τ,

QF = ∫∫qndFdτ.

Fτ

С учетом соотношения (2.8) и уравнения (2.4) получим

QF = ∫∫[qx cos(nr, xr)+ qy cos(nr, yr)+ qz cos(nr, zr)]dFdτ =

Применим к этому интегралу теорему Остроградского– Гаусса:

координатах х, у, z.

Действие внутренних источников мощностью qv обеспечит выделение теплоты

QV = ∫∫qvdVdτ,

Vτ

а изменение энтальпии среды за время τ в изобарном процессе р = const составит

где ρcp — объемная удельная изобарная теплоемкость среды (далее индекс “р” везде опущен).

Подставляя QF, QV и ∆H в исходное уравнение (2.6), получим

V∫∫τqvdVdτ+V∫∫τλ 2TdVdτ =V∫∫τρc ∂∂TτdVdτ,

oткуда

ρc ∂∂Tτ = λ 2T + qV ,

или

которая характеризует ее тепловую инерционность (впервые термин "температуропроводность" использовал Д. Максвелл).

Равенство (2.10) — уравнение в частных производных параболического типа, его называют дифференциальным уравнением теплопроводности, или дифференциальным уравнением Фурье.

В стационарных задачах теплопроводности ∂∂Tτ = 0 , уравнение

(2.10) принимает вид

В одно- и двумерных задачах соответствующие члены в операторе Лапласа приравнивают нулю; если в среде нет внутренних тепловых источников, то полагают qV = 0.

Уравнение (2.10) можно записать в различных системах координат; в частности, для областей с осевой симметрией удобно использовать цилиндрические координаты r, ϕ, z; дифференциальное уравнение теплопроводности выглядит при этом так:

2.2.4. Условия однозначности

Уравнение теплопроводности (2.10) является весьма общим: при его выводе мы не накладывали ограничений на форму области, распределение плотности теплового потока по поверхности F и т. д.

Именно в силу своей общности дифференциальное уравнение теплопроводности имеет бесконечное множество решений.

Чтобы применить его в расчетах, следует добавить к уравнению

134

(2.10) условия однозначности. Требуется, в первую очередь,

задать форму и размеры, а также теплофизические свойства (λ,

ρ, с) среды. Если теплофизические свойства заданы числами, т. е. в рамках решаемой задачи постоянны, то говорят о линейной задаче теплопроводности. Линейные задачи решаются проще нелинейных, а их результаты обычно обеспечивают приемлемую точность; далее речь пойдет именно о них.

Требуется также знать мощность внутренних источников qV. Однако задачи с внутренними источниками применительно к транспортным системам встречаются достаточно редко, далее везде полагаем qV = 0.

Кроме формы и размеров, необходимо задать начальное

Обычно начальное распределение температур считают равномерным.

В стационарных задачах теплопроводности начальное состояние среды "давно забыто", и начальные условия (2.13), (2.14) в краевую задачу не входят.

Граничные условия могут быть достаточно сложными; их записывают для совокупности точек Г, лежащих на граничной поверхности Г (т. е. Г F), полагая, что во всех случаях τ ≥ 0.

В теории теплопроводности традиционно выделяют четыре основных вида граничных условий.

Граничные условия I рода (условия Дирихле) задают распределение температуры на границах области и ее изменение во времени:

Граничные условия II рода (условия Неймана) задают распределение плотности теплового потока qг на границах области и ее изменение во времени:

Принимают qг > О при охлаждении среды и qг < 0 — при нагреве.

Граничные условия III рода соответствуют случаю, когда на поверхности происходит конвективный теплообмен с жидкостью или газом, имеющими постоянную температуру (эти условия называют также условиями Ньютона, хотя фактически впервые их использовал Фурье). Условия Ньютона имеют форму

−λ ∂T = α(Tf −Tw ). (2.17)

∂n Г

иназваны так потому, что уравнение (2.17) совпадает с законом Ньютона

здесь Tw — температура стенки (поверхности теплообмена); индекс “w” соответствует англ. wall — стенка; Tf — температура жидкости или газа (англ. fluid — жидкость); α — коэффициент теплоотдачи, численно равный плотности теплового потока на граничной поверхности Г, отнесенной к температурному перепаду Tf – Tw между окружающей средой и поверхностью Г. Размерность коэффициента теплоотдачи — Вт/(м2 К). В задачах теплопроводности величину α обычно считают постоянной и заданной3.

3 В формуле (2.17) плотность теплового потока связана с разностью температур линейно, поэтому более строго такие условия теплообмена называют линейными граничными

136

Граничные условия IV рода (условия сопряжения) соответствуют случаю идеального теплового контакта двух сред с теплопроводностями λ1 и λ2:

(в формуле (2.18) полагают, что среда с теплопроводностью λ1 подходит к границе Г слева, со стороны Г–0, а среда с теплопроводностью λ2 — справа, со стороны Г + 0).

Заметим, что условия (2.16)–(2.18) содержат члены вида

общие, все другие формы граничных условий можно считать их частными случаями.

Многие практически важные задачи имеют сложную форму граничных условий. В справочной литературе приведены способы расчета систем, на границе которых одновременно действует несколько видов граничных условий (методы суперпозиции).

Отметим, что эти методы справедливы только для линейных задач теплопроводности.

Уравнение теплопроводности (2.10) совместно с условиями однозначности образует краевую задачу теплопроводности (краевую задачу Фурье). Доказано, что краевая задача теплопроводности имеет единственное решение в виде уравнения поля температуры (2.1). Кроме того, из уравнения (2.1) удается получать значения величин q, Q и Qτ, для чего дополнительно используют закон Фурье: если уравнение вида T (x, y, z, τ) известно,

то можно рассчитать производные ∂T ∂x,∂T ∂y ,∂T ∂z , взять интегралы по поверхности, времени и т. д.

условиями III рода. Далее слово "линейные" опускаем, предполагая,

что α = const.

137

Правильная постановка, решение и анализ краевой задачи теплопроводности позволяют ответить и на более общие вопросы, важные как для конструирования, так и для эксплуатации транспортных систем; например:

–как долго будет нагреваться элемент конструкции до заданной температуры и за какое время сможет затем охладиться?

–обеспечивают ли выбранные конструкционные и теплоизоляционные материалы заданный (или приемлемый) тепловой режим?

–можно ли уменьшить материалоемкость и массу конструкции, не нарушив ее теплового режима?

–есть ли резервы для увеличения мощности агрегата, как он (и машина в целом) поведет себя в нештатной ситуации (при пожаре, затоплении отсека водой и т. д.)?

Круг подобных вопросов широк, поэтому задачи теплопроводности представляют для инженеров-транспортников значительный интерес.

Решить задачу Фурье в полной постановке обычно достаточно сложно; намного удобнее найти “готовое” решение в справочной литературе. Таких решений чрезвычайно много, поэтому использование литературы в инженерных расчетах теплопроводности заслуживает особого внимания.

2.2.5. Модели тел в задачах теплопроводности

Элементы конструкций обычно имеют достаточно сложную форму, однако, допуская некоторые упрощения, можно заменить их телами канонической формы, для которых получены многочисленные решения краевой задачи теплопроводности. Это:

пластины (неограниченные плоские стенки), у которых два габаритных размера a и b значительно превышают третий размер δ

(рис. 74,а);

138

Рис. 74.

цилиндры, у которых габаритные размеры в двух направлениях близки к D, а в третьем — к l, причем l >> D (рис. 74,б); цилиндр может быть полым (d < D) или сплошным (d = 0);

шары (или шаровые оболочки), у которых во всех направлениях размеры почти совпадают и близки к D (рис. 74,в), а

0 ≤ d < D.

В транспортной технике пластины — стенки кузова, плоские слои теплоизоляции, ограждения отсеков; цилиндры — трубопроводы, валы, оси; к шаровой оболочке приближаются многие специальные транспортные средства (капсулы космических аппаратов, батискафы), а также, как ни странно, многие обычные транспортные машины, если их рассматривать не по элементам, а в целом.

Если объем пластины или оболочки V относят к общей площади поверхности F, то величину

называют обобщенным размером тела.

Для пластины, у которой V = V р, F = Fр и b >> δ, h >> δ,

Rp = VFp = 2bhbhδ = δ2 .

p

Для сплошного цилиндра при V = Vc, F = Fc и l >> D,

Для сплошного шара при V = V b, F = F b,

139

D3

Rb = Vb = π 6 = D ,

Fb πD2 6

(в индексах везде используем англ. р1аnе — пластина, cylinder — цилиндр, ball — шар).

Так же оценивают величину R любого реального элемента конструкции или агрегата, после чего решают, к какой группе тел его отнести. Нередко выбор делают интуитивно (и достаточно точно). В сомнительных случаях нужен более сложный анализ или эксперимент.

Часть тел выглядят достаточно массивными (в прямом смысле), причем тепловой поток подводится к их свободной поверхности; таков, например, большой камень, разогреваемый солнцем, или сидение автомобиля, получающее теплоту от тела водителя (рис. 75,а).

При таком способе нагрева на достаточной глубине х →∞

Рис. 75.

В этом случае говорят о теплопроводности полуограниченного тела (или полупространства). Если считать, что теплота в полуограниченном теле передается только вдоль оси х, то получим другую модель: полуограниченный стержень х > 0,

у которого плотность теплового потока на боковых стенках q = 0

140

(рис. 75,б). Для стержня постановка задачи Фурье будет такой же, как и для полуограниченного слоя.

Обычно во всех телах канонической формы вектор теплового потока направлен вдоль одной из осей, что позволяет использовать одномерное уравнение Фурье. Нередко поверхности выполняют

Рис. 76.

оребренными (рис. 76); ребра участвуют в теплообмене со средой при граничных условиях III рода. Поверхность с ребрами позволяет отвести от тела значительно большую теплоту, чем неоребренная поверхность. Тепловой расчет оребрения рассмотрим в разделе

2.3.3.

2.3.СТАЦИОНАРНАЯ ТЕПЛОПРОВОДНОСТЬ

2.3.1.Теплопроводность пластин и оболочек

Рассмотрим пластину (рис. 77) толщиной δ, в сечении которой отсутствуют внутренние тепловые источники (qv = 0), а теплопроводность λ постоянна. Температуры на поверхностях пластины Тw1и Тw2 также постоянны, причем Тw1> Тw2.

Таким образом, требуется решить стационарную одномерную задачу теплопроводности при граничных условиях I рода: