
- •§1. Основные понятия. 4
- •Вариант практической цели управления.
- •§2 Статические свойства сау. (Проблема точности). Основные принципы ау. Общая структура сау.
- •Общая структура сау.
- •§3. Классификация сау.
- •§4. Дифференциальные уравнения и передаточные функции линейных систем.
- •Дифференциальное уравнение линейной непрерывной системы n-го порядка.
- •§5. Связь между входом и выходом системы во временной области.
- •§6. Передаточные функции типовых соединений звеньев.
- •§7. Частотные характеристики (чх) динамической системы.
- •Математические модели входа и выхода.
- •Физический смысл чпф.
- •§8. Частотные и временные характеристики типовых звеньев сау.
- •§9. Нетиповые и специальные звенья.
- •Неминимально-фазовые звенья
- •§10. Лах последовательно соединенных звеньев.
- •§11. Определение фазы по лах минимально-фазовой системы.
- •§12. Детализированные структурные схемы и сигнальные графы.
- •§13. Эквивалентные преобразования структурных схем линейной системы.
- •§14. Теорема Мейсена.
- •§15. Приближенное построение лчх параллельных соединений звеньев.
- •§16. Математические модели динамических систем в форме переменных состояния.
- •Запись уравнений переменных состояния по дсс.
- •§17. Линеаризация уравнений динамических систем.
- •Практические способы линеаризации.
- •§18. Передаточная матрица динамической системы.
- •§19. Управляемая каноническая форма.
- •§20. Устойчивость линейных систем.
- •Теоремы первого метода Ляпунова.
- •§21. Суждение об устойчивости линейной системы по коэффициентам характеристического полинома.
- •Критерии устойчивости Гурвица.
- •§22. Частотный критерий устойчивости Найквиста.
- •Критерий Найквиста для афх.
- •Критерий Найквиста для лчх.
- •§23. Качество сау.
- •Показатели качества переходной характеристики.
- •Частотные оценки качества.
- •Запасы устойчивости.
- •Показатель колебательности.
- •Полоса пропускания
- •Корневые оценки качества.
- •Стандартные полиномы .
- •§24. Точность сау.
- •Передаточная функция для ошибки.
- •Коэффициент ошибок.
- •Способы нахождения коэффициентов ошибок.
- •Способы определения порядка астатизма.
- •Добротность.
- •§ 25. Синтез сау.
- •Классический алгоритм синтеза.
- •Методы последовательной коррекции. Типовые последовательные ку.
- •Параллельная коррекция.
- •§26. Системы подчиненного регулирования (спр).
- •Стандартная настройка на оптимум по модулю (ом).
- •Настройка на симметричный оптимум (см).
- •Достоинства спр (систем подчиненного регулирования).
- •§27. Модальное управление.
- •Методика синтеза модального регулятора.
Теоремы первого метода Ляпунова.
Они позволяют судить об устойчивости
состояния равновесия нелинейной системы
![]() (20.14)
(20.14)
по уравнению![]() (20.15)
(20.15)
полученному линеаризацией функции
![]() в точке
в точке![]() (замечание:
(замечание:![]() ).
).
Теорема 20.4. Если все собственные значения
матрицы
![]() находятся в левой полуплоскости, то
состояние
находятся в левой полуплоскости, то
состояние![]() системы (20.14) асимптотически устойчиво.
Таким образом, отброшенные при
линеаризации члены не могут сделать
систему неустойчивой.
системы (20.14) асимптотически устойчиво.
Таким образом, отброшенные при
линеаризации члены не могут сделать
систему неустойчивой.
Теорема 20.5. Если среди собственных
значений матрицы
![]() хотя бы одно находится в правой
полуплоскости, то состояние
хотя бы одно находится в правой
полуплоскости, то состояние![]() системы (20.14) неустойчиво.
системы (20.14) неустойчиво.
Теорема 20.6. Если среди собственных
значений матрицы
![]() хотя бы одно имеет нулевую вещественную
часть, то по уравнению (20.15) нельзя судить
об устойчивости состояния
хотя бы одно имеет нулевую вещественную
часть, то по уравнению (20.15) нельзя судить
об устойчивости состояния![]() системы (20.14). Таким образом, надо
анализировать уравнение (29.14).
системы (20.14). Таким образом, надо
анализировать уравнение (29.14).
§21. Суждение об устойчивости линейной системы по коэффициентам характеристического полинома.
Вследствие трудности определения
корней характеристического полином
для
![]() и не конструктивности прямых (корневых)
методов анализа устойчивости (неясно,
что нужно сделать, чтобы неустойчивую
систему сделать устойчивой). Широкое
применение получили косвенные методы
анализа устойчивости – критерии
устойчивости:
и не конструктивности прямых (корневых)
методов анализа устойчивости (неясно,
что нужно сделать, чтобы неустойчивую
систему сделать устойчивой). Широкое
применение получили косвенные методы
анализа устойчивости – критерии
устойчивости:
алгебраические (Столье, Гурвица, Льенара-Шинара и др.);
частотные (Найквиста, Михайлова);
Теорема 21.1. Необходимый критерий
устойчивости Столье. Пусть система
![]() порядка имеет характеристический
полином
порядка имеет характеристический
полином![]() (21.1)
(21.1)
Если система асимптотически устойчива,
то все коэффициенты в (21.1) устойчивы:
![]() для всех
для всех![]() .
.
Доказательство: пусть система
асимптотически устойчива, тогда согласно
теореме (20.2) все корни
![]() левые, т.е.
левые, т.е.![]() или
или![]() .
Полагая, что в (21.1)
.
Полагая, что в (21.1)![]() .
.
![]()
![]()
Следовательно,
![]() для всех
для всех![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Невыполнение условия теоремы означает
отсутствие асимптотической устойчивости
(доказывается от противного). Выполнение
условия теоремы не означает не
асимптотической устойчивости и не
устойчивости по Ляпунову. В силу
необходимого характера теоремы (21.1).
Если среди
![]() хотя бы один отрицателен, то система
неустойчива, поскольку это может
означать апериодическую границу
устойчивости. Если система находится
на апериодической границе устойчивости,
то
хотя бы один отрицателен, то система
неустойчива, поскольку это может
означать апериодическую границу
устойчивости. Если система находится
на апериодической границе устойчивости,
то![]() .
Действительно:
.
Действительно:![]()
![]() даёт
корень
даёт
корень![]()
![]() Гурвицев
полином имеет только левые корни.
Гурвицев
полином имеет только левые корни.
Если равен нулю какой-нибудь другой из
коэффициентов, то система неустойчива.
Исключение система
![]() порядка
порядка![]() колебательная
граница устойчивости.
колебательная
граница устойчивости.
Теорема 21.2. Для систем
![]() и
и![]() порядка положительность коэффициентов
характеристического полинома является
не только необходимым, но и достаточным
условием асимптотической устойчивости.
порядка положительность коэффициентов
характеристического полинома является
не только необходимым, но и достаточным
условием асимптотической устойчивости.
Доказательство: непосредственный анализ вещественных частей характеристического полинома.
Критерии устойчивости Гурвица.
Теорема 21.3. Для асимптотической
устойчивости системы с характеристическим
полиномом (21.1) необходимо и достаточно,
чтобы при
![]() были положительны все главные диагональные
миноры матрицы Гурвица
были положительны все главные диагональные
миноры матрицы Гурвица![]() :
:

![]()
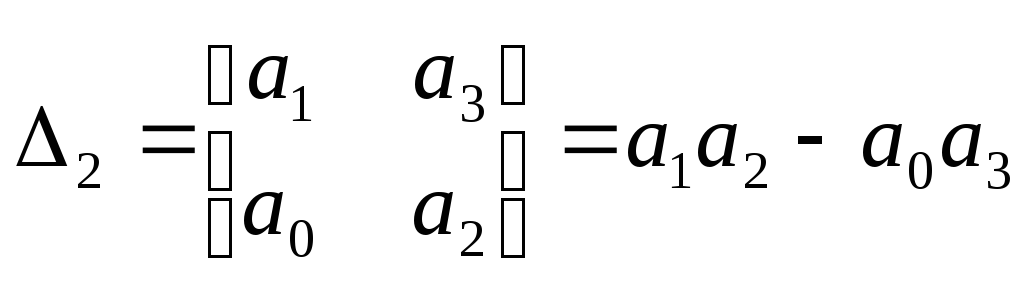
![]()
![]()
Правило составления матрицы
![]() :
:
По главной диагонали выписываем коэффициенты характеристического полинома с
 по
по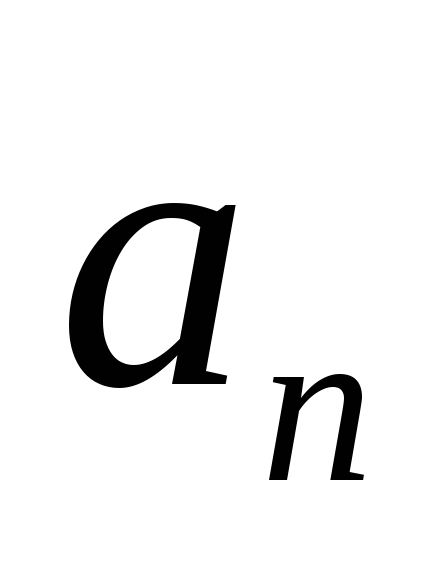 (
(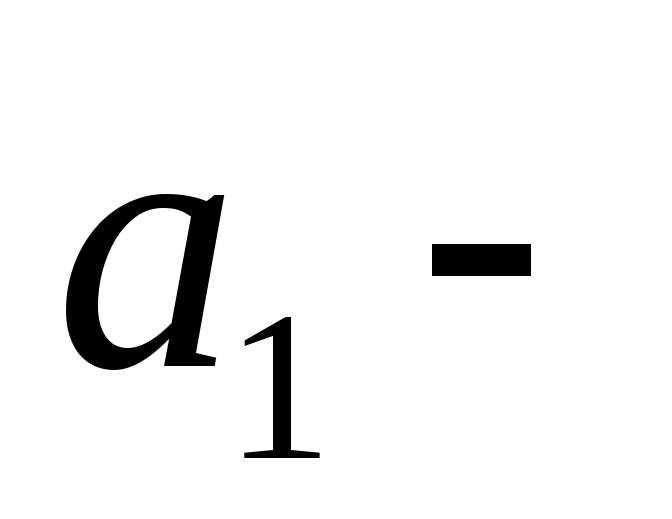 коэффициенты
при
коэффициенты
при );
);Заполняем строки так, чтобы чередовались строки с нечетными и четными индексами элементов.
Элементы с индексами большими
 и меньшими нуля заменяются на ноль.
и меньшими нуля заменяются на ноль.
Частные случаи:
![]()
![]()
![]()
![]()
![]()
![]()
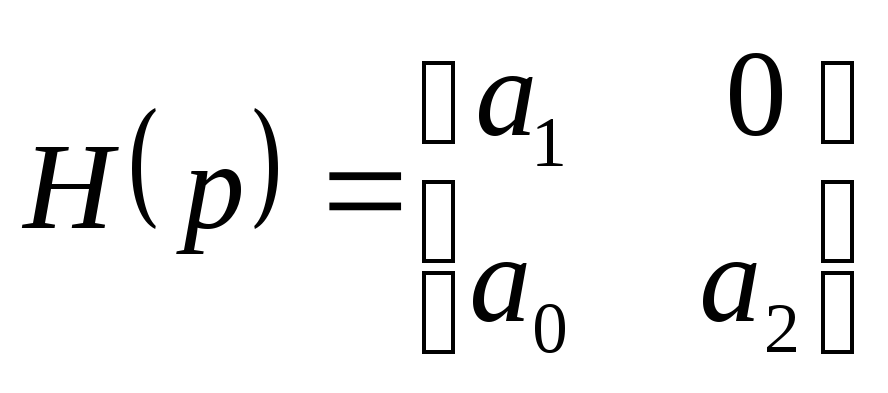
![]()

меньше нельзя (смотри критерий Столье)
Вывод: смотри теорему 21.1.
![]()
![]()
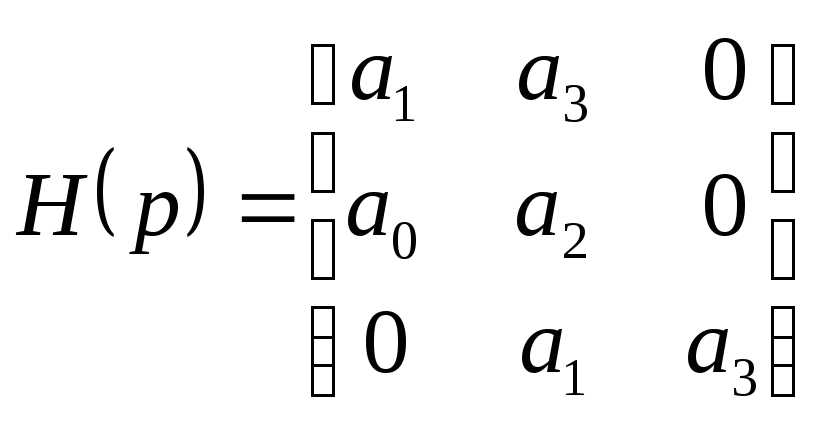
![]()
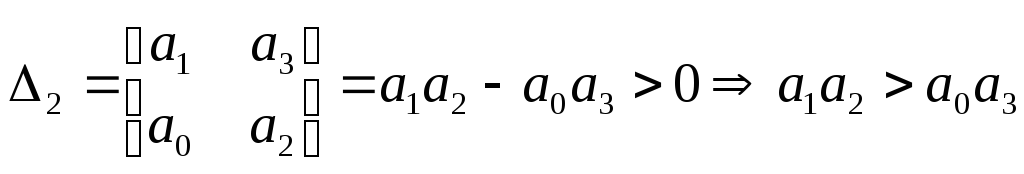
![]()
Таким образом, условия критерия Гурвица
для систем
![]() порядка таковы, что все коэффициенты
порядка таковы, что все коэффициенты![]() и выполняется
и выполняется![]() .
.
Критические случаи:
![]()
Поскольку
![]() то различают три случая:
то различают три случая:
![]() (и остальные
(и остальные![]() )
апериодическая граница устойчивости.
)
апериодическая граница устойчивости.
![]() (и остальные
(и остальные![]() )
колебательная граница устойчивости.
)
колебательная граница устойчивости.
![]() (и остальные
(и остальные![]() )
апериодическая граница устойчивости.
)
апериодическая граница устойчивости.
