§18. Передаточная матрица динамической системы.

(18.1)

(18.2)

Поскольку вход и выход векторы, то вместо понятия передаточной функции необходимо рассматривать более общее понятие передаточной матрицы (ПМ).

Преобразуем (18.1) и (18.2) по Лапласу при ННУ.

(18.3)

(18.4)

Определение 18.1. Матрица размераудовлетворяющая уравнению(18.5)

называется передаточной матрицей или просто передаточной матрицей (ПМ).

Определение 18.2. Матрица размераудовлетворяющая уравнению(18.6)

называется матрицей подсостояния.

Сравнивая (18.5) и (18.4), а также (18.6) и (18.3) находим:

(18.7)

(18.8)

Запишем компонентусогласно (18.5)

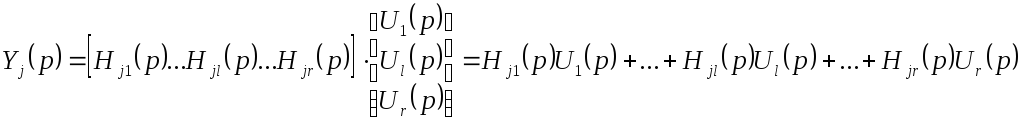
строка.

Вывод: Элемент стоящий встроке истолбце передаточной матрицыесть обычная передаточная функция отвхода квыходу.

Для системы с одним входом и одним выходом передаточная матрица вырождается в передаточную функцию.

§19. Управляемая каноническая форма.

При различном выборе переменных состояния получаются различные уравнения в форме переменных состояния.

Пусть ивекторы состояния в двух различных базисах одного и того же линейного пространства. При этом они связаны не особенным преобразованием.

(19.1)

неособенная матрица.

Найдем связь между матрицами для обоих описаний. Подставимиз (19.1) в (19.2).

(19.6)

(19.7)

Сравнивая (19.6) и (19.7) с (19.4) и(19.5) получаем:

(19.8)

Отсюда:

(19.9)

Преобразования вида преобразования подобных. С его помощью получать различные специальные (канонические) формы матриц и уравнений.

Например:

Если , где, асобственный вектор матрицысоответствующий собственному значению(здесь говорим о случае, когда всепопарно различные, т.е. простые), то.

Рассмотрим УКФ, она характеризуется следующим видом матрицы системы:

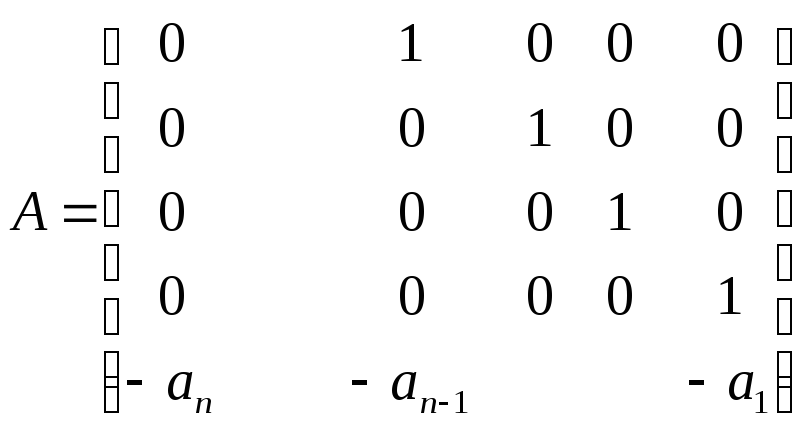(19.10)

где коэффициенты приведенного характеристического полинома.

(19.11)

Рассмотрим получение УКФ по ПФ системы с одним входом и одним выходом.

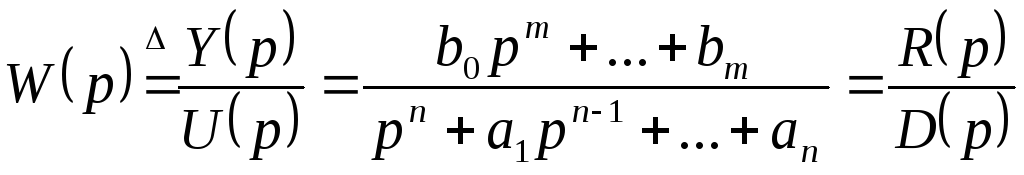(19.12)

1. , т.е.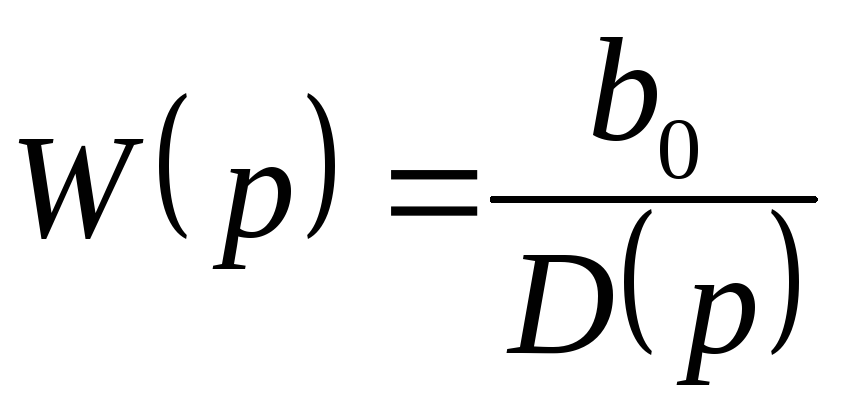

Для получения УКФ в качестве переменных состояния выбирают выходную переменную и все ее производные до включительно.

(19.13)

Таким образом (19.14)

Поэтому из (19.13) сразу получаются все уравнения состояния кроме последнего (смотри (19.14)), а также уравнение выхода (19.15)

Последнее уравнение состояния получаем из передаточной функции переходом во временную область.

(19.16)

На основании (19.14. … 19.16) получаем

где матрица имеет форму (19.10), а матрицыитаковы:

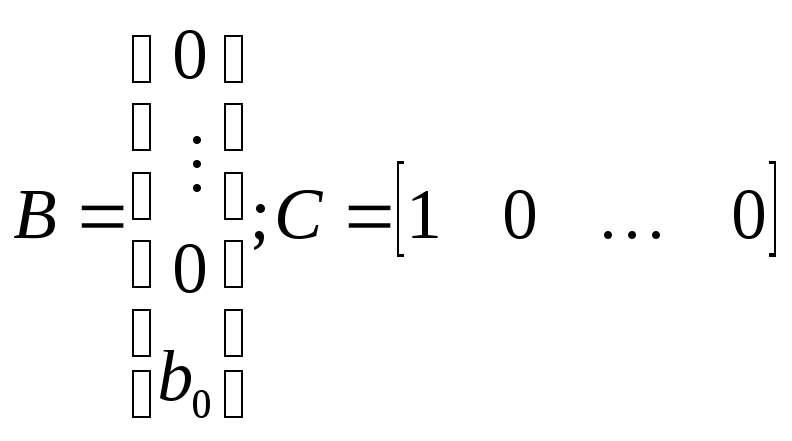(19.17)

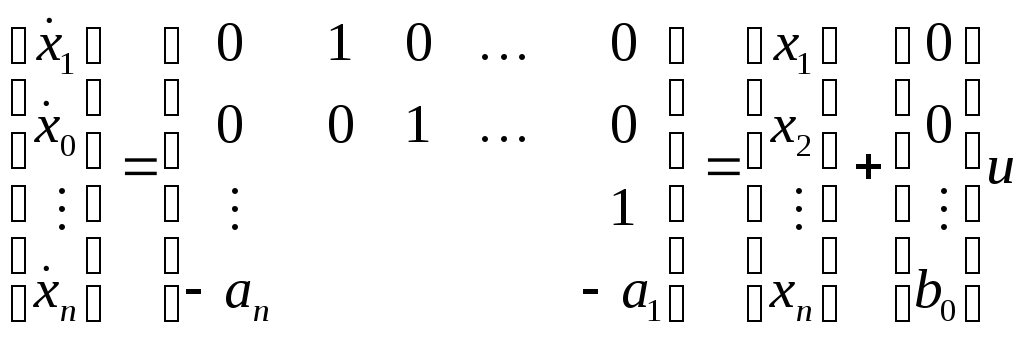
Уравнениям УКФ соответствует структурная схема.

2. Передаточная функция (19.12).

В этом случае выбирать в качестве переменных состояния нельзя, поскольку в последнем уравнении состояния появится производная от входного воздействия благодаря числителю ПФ.

Поэтому для получения УКФ поступают следующим образом: Поступают, что по аналогии с (19.14) первые уравнения имеют вид:

(19.18)

Кроме того (19.19)

В этом случае последнее уравнение состояния примет вид:

(19.20)

Тогда матрица имеет прежний вид (19.10), аитаковы:

(19.21)

Анализ и синтез САУ.

§20. Устойчивость линейных систем.

Решения матричного уравнения

(20.1)

дается формулой Коши

(20.2)

где переходная матрица представляет собой матричную экспоненту:

(20.3)

определенную как ряд:

(20.4)

В частности для свободной системы

и

Удобный способ нахождения матричной экспоненты:

(20.5)

Рассмотрим дифференциальное уравнение вида

(20.6)

Любое частное решение вызванное начальными условиямиможет быть названо невозмущенным движением, тогда любое другое решение порожденное другими начальными условияминазывается возмущенным движением. Эти решения можно изображать в виде траекторий в фазовом пространстве или в расширенном фазовом пространстве.

Пусть, например: и пусть невозмущенным считается движение порожденное начальным условием, т.е. тривиальное решение. Тогда траектории могут иметь следующий вид:

Определение 20.1. Невозмущенное движение системы (20.6) называется устойчивым по Лапласу, если для любогонайдется, такое что изследуетдля всех. В противном случае оно называется неустойчивым. Неустойчивому движению соответствует траектория уходящая в бесконечность.

Определение 20.2. Невозмущенное движение называется асимптотически устойчивым если:

1. оно устойчиво по Ляпунову

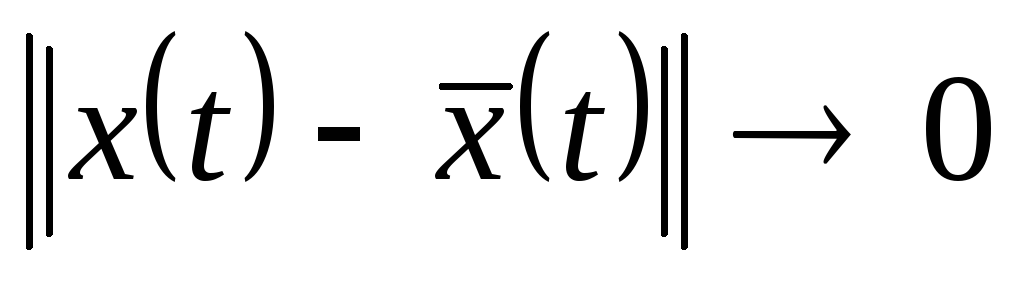2. при.

Устойчивость состояния равновесия является частным случаем рассмотренной выше устойчивости при постоянно действующем возмущении при .

Определение 20.3. Состоянием равновесия называется такое состояние, в котором система, не будучи подвержена внешним возмущениям, может оставаться сколь угодно.

Определение 20.3.а. Вектор называется состоянием равновесия системы(20.7)

(свободной системы), если (20.8)

Пояснение: пусть при и, тогда. Следовательно,для всех. Следовательно,состояние равновесия.

Если определитель матрицы , то система (20.7) имеет единственное состояние равновесия(следует из (20.8) при умножении обеих частей на).

Если , то система имеет бесконечное множество состояний равновесия.

Среди собственных значений матрица имеет, по крайней мере, одно нулевое значение. Можно сказать, что состоянию равновесиясоответствует невозмущенное движениепри начальном условии.

Теорема 20.1. Для устойчивости (асимптотической устойчивости) всех решений уравнения (20.6) необходимо и достаточно, чтобы было устойчиво (асимптотически устойчиво) какое-нибудь тривиальное решение (например ) уравнения (20.7). Таким образом, свойство устойчивости зависит только от матрицы. Поэтому только для линейных систем принято говорить не только об устойчивости каких-либо движений и устойчивости состояния равновесия, но и об устойчивости самой системы.

Пусть система описывается уравнением (20.7) и имеет характеристический полином (20.9)

Теорема 20.2. (основная теорема об асимптотической устойчивости). Для асимптотической устойчивости системы необходимо и достаточно, чтобы все собственные значения матрицы и корни характеристического полиномалежали строго слева от мнимой оси.

, для всех(20.10)

Замечание: матрица и полиномудовлетворяющие (20.10) называются Гурвицевыми или устойчивыми.

Доказательство: (для случая простых собственных значений).

Достаточность: пусть выполняется (20.10), рассмотрим разные случаи:

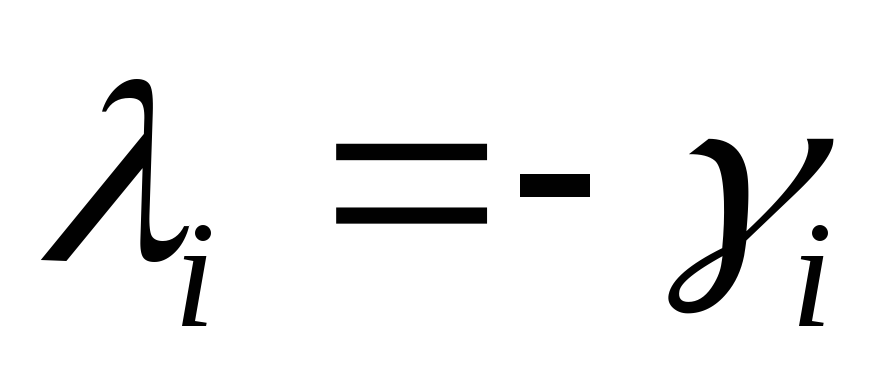
1. . С помощью преобразованияприведем уравнение (20.7) к виду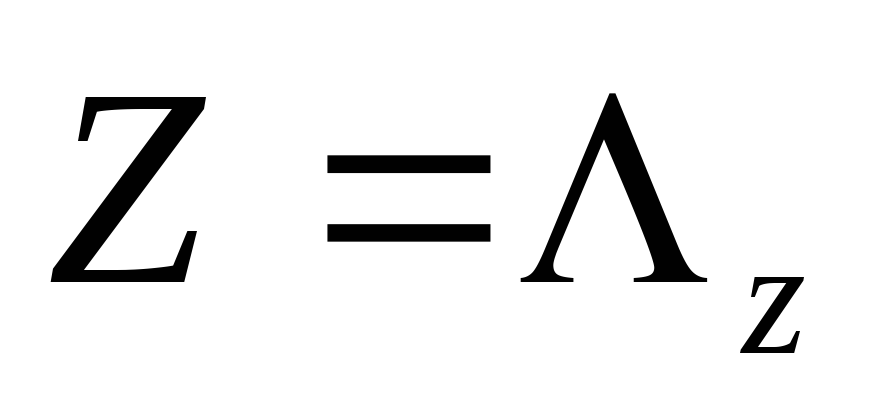(20.11) где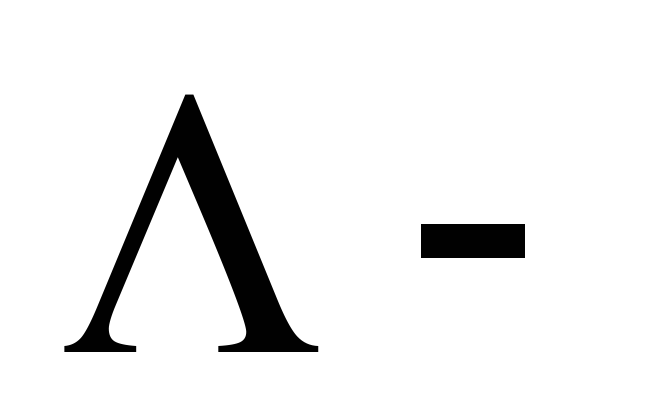диагональная матрица. Отсюда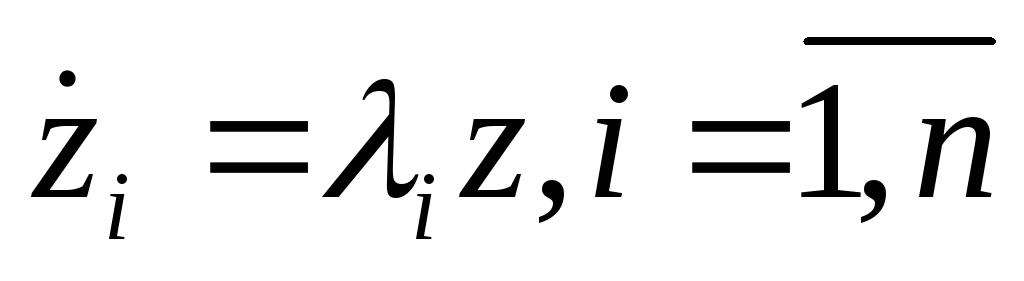(20.12) Для этого случая имеем:

при

2. 

Тогда

при(поскольку огибающая стремится к нулю).

Итак, присистема асимптотически устойчива.

Необходимость: пусть система асимптотически устойчива. Допустим, что среди имеется, по крайней мере, хотя бы одно:

• 

при

• ;

• 

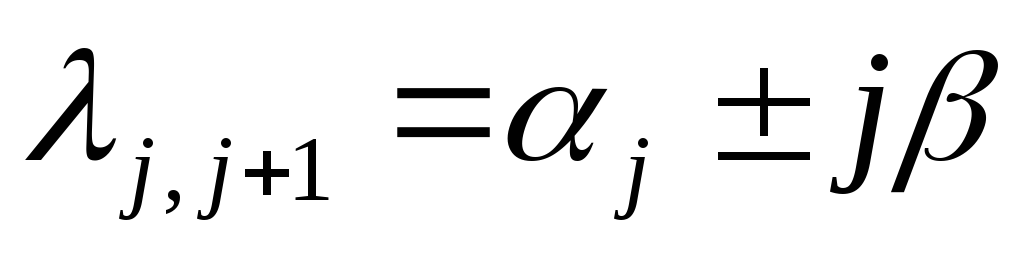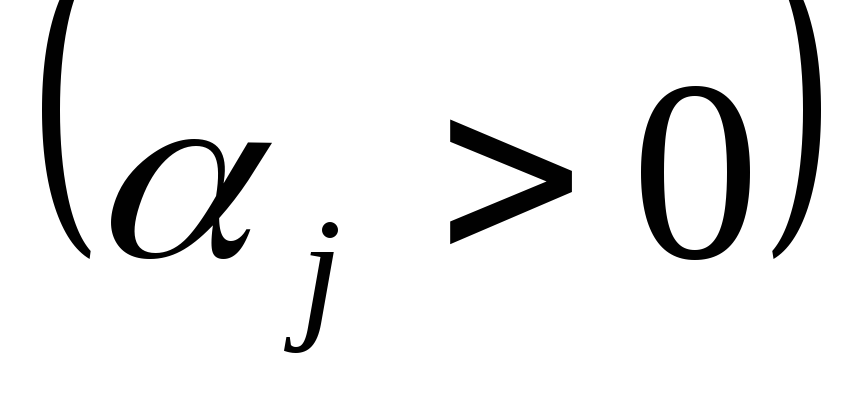
(так как)

• ;

Таким образом, при, что противоречит допущению об асимптотическом движении. А это доказывает необходимость.

Если система не является асимптотически устойчивой, то она находится на границе устойчивости, что соответствует понятию устойчивости по Ляпунову.

Теорема 20.3. (без доказательства). Нулевое решение уравнения(20.13)

устойчиво по Ляпунову если:

• все собственные значения матрицы 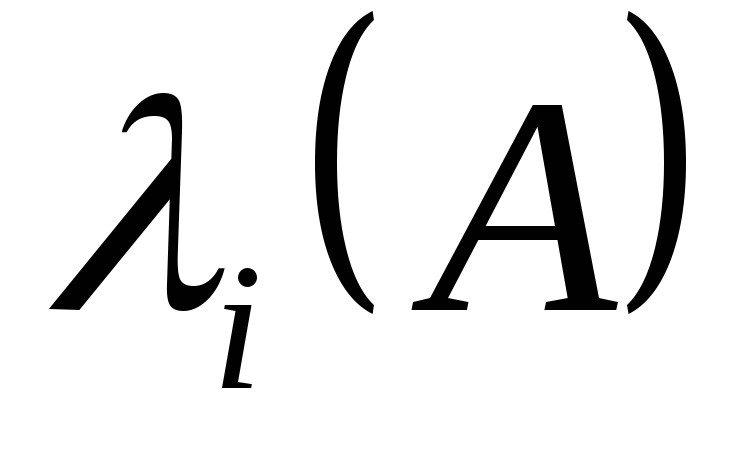имеют неположительные вещественные части.

• собственные значения с нулевой вещественной частью, являются простыми корнями минимального многочлена 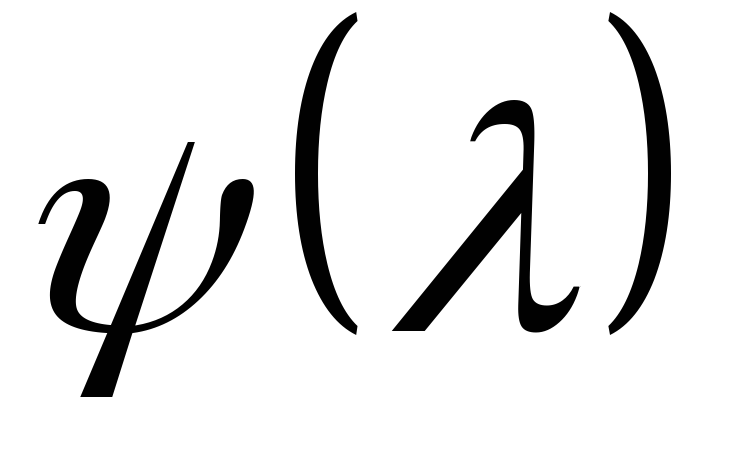матрицы. И неустойчива, если хотя бы одно из условий не выполняется.

Пример 20.1. Рассмотрим две системы второго порядка

Характеристический полином:

Присоединенная матрица:

Наибольший общий делитель:

простой корень.

двукратный корень.

Система устойчива по Ляпунову Система неустойчива по Ляпунову

Следствие 1. Достаточное условие неустойчивости. Если среди имеется хотя бы одна с положительной вещественной частью, то система неустойчива.

Следствие 2. Если среди одно нулевое, а остальные – левые, то система устойчива по Ляпунову, причём говорят, что она находится на границе устойчивости апериодического типа. Это означает, что по окончанию переходного процесса хотя бы одна из переменных системы принимает постоянное значение, вообще говоря, отличное от нуля.

Следствие 3. Если среди имеется пара чисто мнимых, а остальные – левые, то система устойчива по Ляпунову, причём говорят, что она находится на границе устойчивости, это означает, что хотя бы одна переменная совершает незатухающие гармонические колебания.