В. 6. Производная степенно-показательной функции

Производная степенно-показательной функции :

Т.е. для того чтобы найти производную степенно-показательной функции, нужно сначала продифференцировать её как степенную (формула (3)), затем как показательную (формула (7)) и полученные результаты сложить.

Пример 2. Вычислить производную функции .

Решение. .

П роизводная неявной функции F(x,y)=0 получается дифференцированием обеих частей уравнения, рассматривая y как функцию от x , а затем из полученного уравнения находится y`.

Пример 3. Найти производную от неявной функции x² +3xy + y² + 1 =0 и вычислить y` в точке (2; -1).

Решение. Дифференцируя по x, получаем: отсюда

. Подставим x =2 , y = -1, получим .

В.7. Производные высших порядков

Производная называется производной 1-го порядка. Однако производная сама является функцией, которая также может иметь производную.

Производная n-го порядка называется производная от производной (n-1)-го порядка:

.

Обозначается : и т.д.

Механический смысл 2-й производной: 2-ая производная пути по времени равна ускорению точки в момент t₀.

В.9. Приложения производной

9.1. Правило Лопиталя

Правило Лопиталя. Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.

Другими словами, если имеется неопределенность или , то

Пример 4. Найти предел, используя правило Лопиталя: .

Решение. Имеем неопределенность вида . Применяя правило Лопиталя, получим:

= . Неопределенность вида по-прежнему сохраняется. Применим правило еще раз: = .

Ответ: 1.

9.2. Возрастание и убывание функции. Экстремум функции

Теорема (достаточное условие возрастания функции). Если производная дифференцируемой функции положительна внутри некоторого промежутка X,то функция возрастает на этом промежутке.

Теорема (достаточное условие убывание функции). Если производная дифференцируемой функции отрицательна внутри некоторого промежутка X, то функция убывает на этом промежутке.

Необходимое условие монотонности более слабое: если функция возрастает (убывает) на некотором промежутке X, то можно лишь утверждать, что производная неотрицательна (неположительна) на этом промежутке: , т.е. в отдельных точках производная монотонной функции может равняться нулю.

Например, функция y=x³ монотонно возрастает на всей числовой оси, но при x=0

Точка x₀ называется точкой максимума функции ƒ(x),если в некоторой окрестности точки x₀ выполняется неравенство ƒ(x₀) ≥ ƒ(x).

Точка x₁называется точкой минимума функции ƒ(x), если в некоторой окрестности точки x₁ выполняется неравенство ƒ(x₁) ≤ ƒ(x).

Значения функции в точках x₀ и x₁ называются соответственно максимумом и минимумом функции. Их объединяют общим термином – экстремум функции. Его также называют локальным экстремумом , поскольку понятие экстремума связано лишь с достаточно малой окрестностью точки x₀ На одном промежутке функция может иметь несколько экстремумов, причем минимум в одной точке может оказаться больше максимума в другой точке.

Е сли в точке x₀ дифференцируемая функция имеет экстремум, то в некоторой окрестности этой точки выполнены условия теоремы Ферма. Следовательно, . Но функция может иметь экстремум и в точках, в которых она не дифференцируема.

О тсюда необходимое условие экстремума: для того, чтобы функция y= f(x) имела экстремум в точке x₀ , необходимо, чтобы её производная в этой точки равнялась нулю или не существовала.

(Экстремум в точке x =0, но функция здесь не дифференцируемая)

(Производная равна нулю при x=0, но экстремума нет)

Точки в которых выполнено необходимое условие экстремума, называются критическими (стационарными). Их также называют точками, подозрительными на экстремум. Одна критическая точка вовсе не обязательно является точкой экстремума.

Таким образом, для нахождения экстремумов функции требуется дополнительное исследование критических точек, т.е. нужно достаточное условие экстремума.

Теорема (первое достаточное условие экстремума). Если при переходе через точку x₀ производная дифференцируемой функции меняет свой знак с плюса на минус, то точка x₀ есть точка максимума функции y=ƒ(x), а если с минуса на плюс, то точка минимума .

Схема исследование функции y=ƒ(x) на экстремум:

1. Найти .

2. Найти критические точки функции, в которых =0 или не существует.

3. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.

4. Найти экстремумы функции (экстремальные значение функции).

Пример 5. Исследовать функцию на экстремум.

Теорема (второе достаточное условие экстремума). Если функция у=ƒ(x) дважды дифференцируема и в некоторой точке x₀ =0, >0, то x₀ есть точка минимума функции y=ƒ(x),если =0, <0, то точка максимума.

Д ля отыскания наибольшего и наименьшего значений функции на отрезке надо найти значения функции в критических точках и на концах отрезка и выбрать из них наименьшее ƒ_min и наибольшее значение ƒ_max.

Е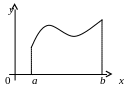 сли функция непрерывна на интервале (а,b), то она может не принимать на нем наибольшего и наименьшего значений. В частности, если дифференцируемая функция на интервале (а,b) имеет лишь одну точку максимума, то наибольшее значение функции совпадает с максимумом этой функции.

Пример 6. Найти наибольшее и наименьшее значения функции у = х³ – 12х на отрезке [0, 5].

Решение. Сначала найдем производную функции: у’ = 3х² – 12.

Затем найдем критические точки, т.е. точки, в которых у’ = 0 или не существует: 3х² – 12 = 0, откуда критические точки х₁ = –2, х₂ = 2. Точка х₁ = –2 не принадлежит отрезку [0, 5], поэтому мы исключаем ее из рассмотрения.

Вычислим значения функции в критической точке х₂ = 2 и на концах интервала и выберем из них наибольшее и наименьшее: у(2) = – 16, у(0) = 0, у(5) = 65.

Ответ: Т.о. наибольшее значение функции на отрезке [0, 5] равно 65, наименьшее равно –16.