В.8. Вычисление пределов

При вычислении пределов используют то, что предел постоянной равен самой постоянной, а также основные теоремы о пределах. Рассмотрим вычисление пределов на примерах.

Приме7.

Применяя теоремы о пределах, получаем:

Пример 8.

Пределы числителя и знаменателя существуют и предел знаменателя не равен нулю. Пользуясь теоремой о пределе частного, получаем:

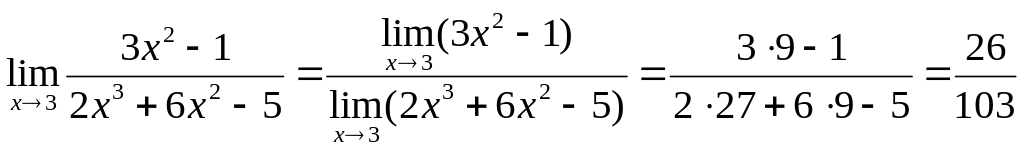
Пример 9.

Непосредственно применять теорему о пределе частного нельзя, т.к. предел знаменателя равен нулю. В числителе имеем ограниченную величину, отличную от нуля. Таким образом, под знаком предела будет произведение ограниченной величины х²-2х+1, отличной от нуля на бесконечно большую величину при х  3 как величину, обратную бесконечно малой. Поэтому

Пример 10.

Здесь также нельзя непосредственно применять теорему о пределе частного, т.к. пределы знаменателя и числителя равны нулю и мы имеем неопределенность вида . В подобных случаях, когда и в числителе и в знаменателе – многочлены, их необходимо разложить на множители, после этого дробь сократить и перейти к пределу:

Пример 11.

Если под знаком предела имеется иррациональность, то для раскрытия неопределенности вида необходимо перенести иррациональность из числителя в знаменатель или из знаменателя в числитель, а иногда и то и другое, полученную дробь сократить и перейти к пределу:

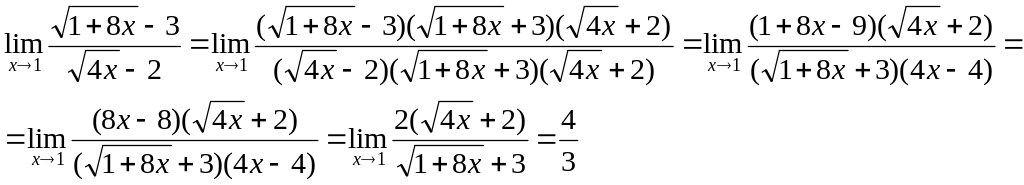
Пример 12.

При х  0 переменная х есть бесконечно малая величина, а   1 при любых значениях х0. Следовательно, величина - произведение бесконечно малой на ограниченную величину – также будет бесконечно малой величиной, поэтому ее предел равен 0.

Пример 13.

Теорему о переделе частного здесь применять нельзя, т.к. числитель и знаменатель конечного предела не имеют. Имеем неопределенность . В подобных случаях для раскрытия неопределенности целесообразно числитель и знаменатель разделить на степень х с наивысшим показателем, а затем перейти к пределу:

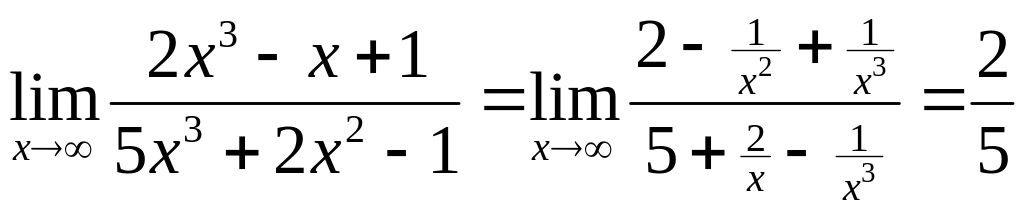
Неопределенность вида  –  раскрывается путем преобразования и сведения их к неопределенности или .

Пример 14.

Пример 15.

Здесь следует рассмотреть два случая:

а)

б)

Если при х  а (х  ) f(x)  1, а (х)  , то говорят, что имеем неопределенность вида 1^. Для раскрытия этой неопределенности используется второй замечательный предел.

Пример 16. Найти .

Решение. Выделим у дроби целую часть:

.

Чтобы использовать второй замечательный предел (или ), обозначим . Тогда при х→∞ у→0, причем . Т.о. = .

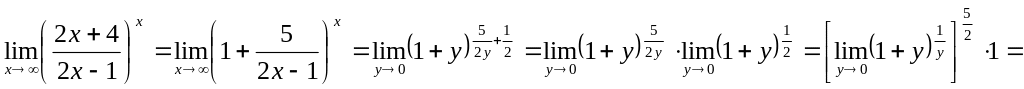Ответ: .

Тема 2. Дифференциальное исчисление функций одной переменной в.1. Задачи, приводящие к производной. Задача о касательной:

Пусть на плоскости ОХY дана непрерывная кривая у=f(х) и необходимо найти уравнение касательной к этой кривой в т. М (х , у ).

Дадим аргументу х приращение и перейдем по кривой у=f(х) от т. М (х ,у ) к т. М (х + ,f(х + ). Проведем секущую М .

Под касательной к кривой у=f(х) в т. М понимают предел положительной секущей М при приближении т. М к М , т. е. при .

Уравнение прямой, проходящей через точку М , имеет вид: у – f(х )=k(х– х₀ ). k -угловой коэффициент может быть найден из : k = tg = . Отсюда – угловой коэффициент касательной.

Задача о скорости движения:

Пусть вдоль некоторой прямой движется точка по закону , где s – пройденный путь, t – время. Надо найти скорость точки в момент t₀.

К моменту пройденный путь составит , а к моменту : . Тогда за время средняя скорость . Чем меньше , тем лучше средняя скорость характеризует движение точки в момент t₀. Поэтому под скоростью в момент t₀ естественно понимать предел средней скорости за промежуток от t₀ до , когда : .