Последовательности точек

Говорят, что при , если для для будет , т.е. при .

Пусть . Тогда при тогда и только тогда, когда при .

1. Пусть при . Возьмём . Тогда N: для будет . Но тогда для при при .

2. Пусть при . Возьмём . Тогда для будет для будет для будет 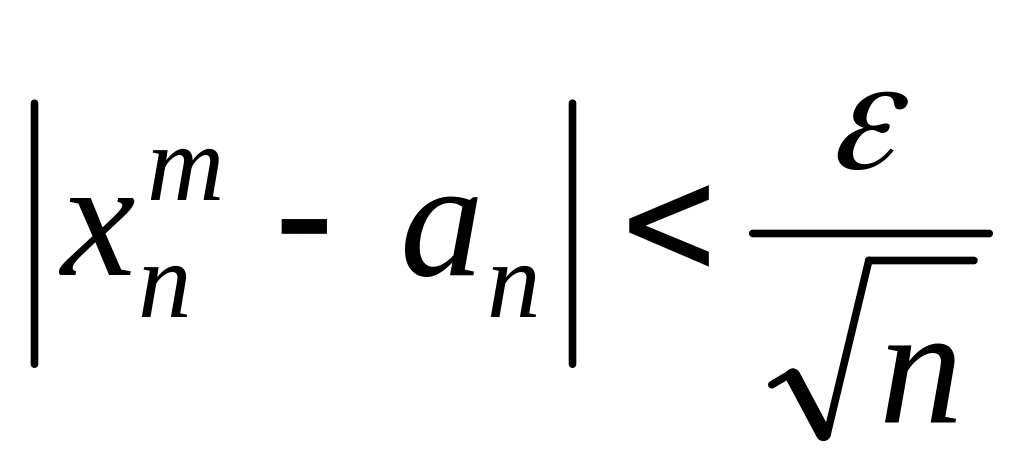. Возьмём . Тогда для будет для , т.е. при .

Лемма Больцано-Вейерштрасса: Из любой ограниченной последовательности точек пространства можно выбрать сходящуюся подпоследовательность.

Пусть ограничена, т.е. . Тогда ограничены: для . По лемме Больцано-Вейерштрасса для последовательности, при . Применим снова эту лемму для . Тогда при . В итоге . Тогда все и, значит, .

Для сходимости к конечному пределу необходима и достаточна фундаментальность , т.е. выполнение условия: для для и будет (речь идёт о конечномерном пространстве).

Функции и их пределы

Пусть , где X – метрическое пространство. Функцией называется однозначное отображение из X во множество чисел.

Пусть – точка, предельная для множества определения функции . Говорят, что , если для при будет выполнено при .

Пусть – точка, предельная для множества определения . Говорят, что , если для для M, удовлетворяющих условию и в которых определена, будет .

Оба определения равносильны.

значит, что множество определения неограниченно и для для будет .

Непрерывность

Функция непрерывна в точке , если и для для и определена будет .

Если добавить условие, что – предельная точка для множества определения , то непрерывна в точке , т.е. при или при .

Если и непрерывны в точке , то и непрерывны в точке (последнее если ).

Теорема о сохранении знака: Если и непрерывна в точке , то существует окрестность при (где определена).

Возьмём . Тогда для M, удовлетворяющих условию будет .

Теорема о непрерывности сложной функции: Пусть заданы функции и пусть непрерывна в точке , а функция непрерывна в точке . Тогда сложная функция будет непрерывна в точке .

Возьмём при . Тогда для будет , т.е. точки , а, значит, по непрерывности , будет , т.е. для при , т.е. , что и означает непрерывность сложной функции .

Т еорема Коши: Пусть определена и непрерывна на связанном множестве и пусть . Тогда для существует точка .

Соединим точки L и K непрерывной кривой . Вдоль этой кривой превращается в сложную функцию , причём и, наконец, непрерывна на . По теореме Коши для для . Но , где и .

Если F – замкнутое множество, и , то .

1. Если – одна и та же точка для m, начиная с некоторого, то .

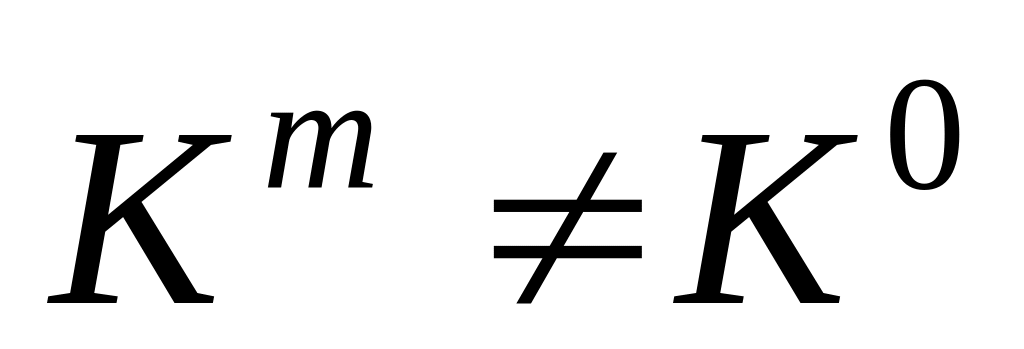2. Если – разные точки, то в любой окрестности лежит точка из . Тогда – предельная точка для F, следовательно, .

I теорема Вейерштрасса: Если непрерывна на замкнутом ограниченном множестве F конечномерного пространства, то ограничена на F.

Пусть неограниченна. Тогда для m натуральных . Т.к. ограничена, то по лемме Больцано-Вейерштрасса, при . Тогда и в точке непрерывна, следовательно, при , что невозможно, т.к. при . Следовательно, ограничена.

II теорема Вейерштрасса: Если непрерывна на замкнутом ограниченном множестве конечномерного пространства F, то достигает на нём своего наибольшего и наименьшего значений.

Пусть . Тогда для n натурального . Выбираем из по лемме Больцано-Вейерштрасса . При этом . Т.к. , то при будет: .

Пусть A – подмножество некоторого метрического пространства X. Тогда («диаметр A»).

Функция называется равномерно непрерывной на множестве , если для для будет .

Теорема Кантора: Если непрерывна на замкнутом ограниченном множестве F конечномерного пространства, то равномерно непрерывна на F.

Если F – замкнутое ограниченное множество конечномерного пространства и непрерывна на F, то для существует разбиение F на подмножества .