
- •II семестр – весенний семестр 2003 года
- •Необходимое и достаточное условия интегрируемости
- •Классы интегрируемых функций
- •Интегралы как функции множества
- •Оценки интегралов
- •Интеграл как функция верхнего предела
- •Приложение определённого интеграла
- •Площади фигур
- •Условная сходимость
- •Ряды со знакопеременными членами
- •Действия над рядами
- •Функциональные ряды и последовательности
- •Признаки равномерной сходимости
- •Степенные ряды
- •Понятие о рядах Фурье
- •Функции нескольких переменных
- •Последовательности точек
- •Дифференцирование функций нескольких переменных
- •Производные и дифференциалы высших порядков
- •Зависимость функций
Математический анализ
Лектор: Юрченко Александр Максимович
II семестр – весенний семестр 2003 года
Определённый интеграл
Пусть дан
![]() .
Разбиением T
отрезка
называется набор точек
.
Разбиением T
отрезка
называется набор точек
![]() или набор отрезков
или набор отрезков
![]() ,
где
,
где
![]() .
Будем обозначать
.
Будем обозначать
![]() .
.
П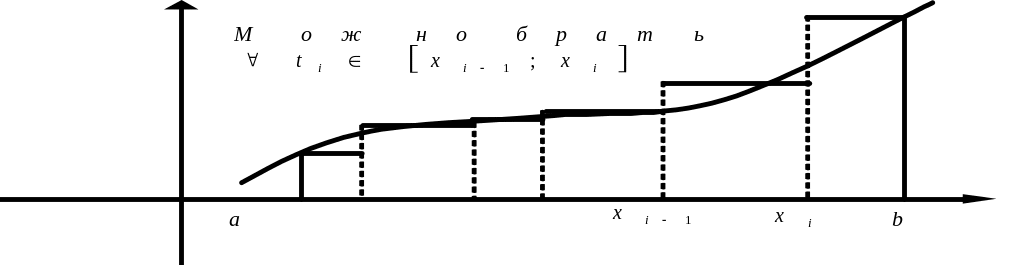 усть
на отрезке
усть
на отрезке
![]() задана функция
задана функция
![]() .
Возьмём некоторое разбиение
.
Возьмём некоторое разбиение
![]() отрезка
и в каждом отрезке
выберем точку
отрезка
и в каждом отрезке
выберем точку
![]() .
Сумма
.
Сумма
![]() называется интегральной.
Число I
называется интегралом
от
,
если для
называется интегральной.
Число I
называется интегралом
от
,
если для
![]()
![]() для всех разбиений T
с
для всех разбиений T
с
![]() при любом выборе точек
будет
при любом выборе точек
будет
![]() (т.е.
(т.е.
![]() ).
Обозначается
).
Обозначается ![]() (интеграл, определённый таким образом,
называется интегралом
Римана).
(интеграл, определённый таким образом,
называется интегралом
Римана).
Если не ограничена на , то неинтегрируема на .
Пусть
не ограничена на
.
Возьмём любое разбиение
![]() .
Тогда
.
Тогда
![]() на
на
![]() не ограничена. Выберем в каждом отрезке
,
где
не ограничена. Выберем в каждом отрезке
,
где
![]() точку
точку
![]() и зафиксируем. Тогда
и зафиксируем. Тогда
![]() ,
где
,
где
![]() пока не выбрано. Возьмём
пока не выбрано. Возьмём
![]() .
Т.к.
не ограничена на
,
то можно выбрать
так, что
.
Т.к.
не ограничена на
,
то можно выбрать
так, что
![]() .
Тогда
.
Тогда
![]() ,
т.е.
,
т.е.
![]() не ограничена и не может иметь предела.
не ограничена и не может иметь предела.
Пример: функция Дирихле
![]() .
Возьмём
.
Возьмём
![]() .
Если все
– рациональные, то
.
Если все
– рациональные, то
![]() ,
а если все
– иррациональные, то
,
а если все
– иррациональные, то
![]() ,
следовательно,
,
следовательно,
![]() неинтегрируема по Риману.
неинтегрируема по Риману.
Необходимое и достаточное условия интегрируемости
Изначально считаем, что на ограничена.
Введём числа
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Т.к.
ограничена, то все эти числа существуют.
.
Т.к.
ограничена, то все эти числа существуют.
Суммы
![]() и
и
![]() – соответственно верхняя
и нижняя суммы Дарбу при разбиении T.
– соответственно верхняя
и нижняя суммы Дарбу при разбиении T.
С войства:
войства:
Для данного разбиения T при
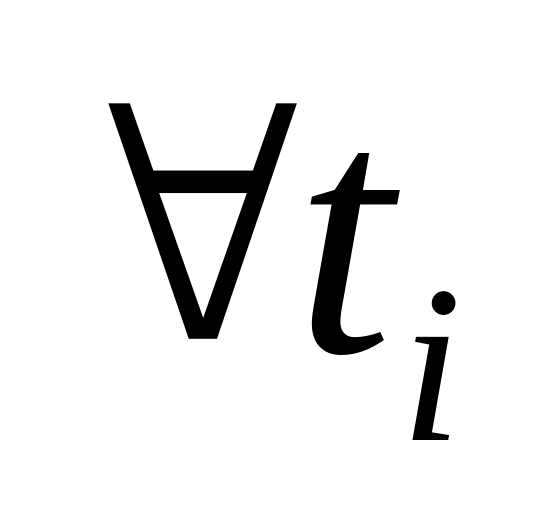 будет
будет
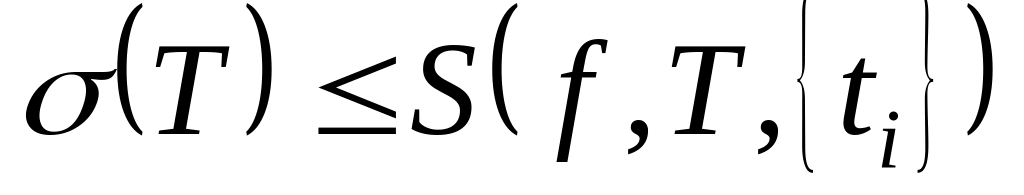 ,
а
,
а
 .
Следует из того, что
.
Следует из того, что
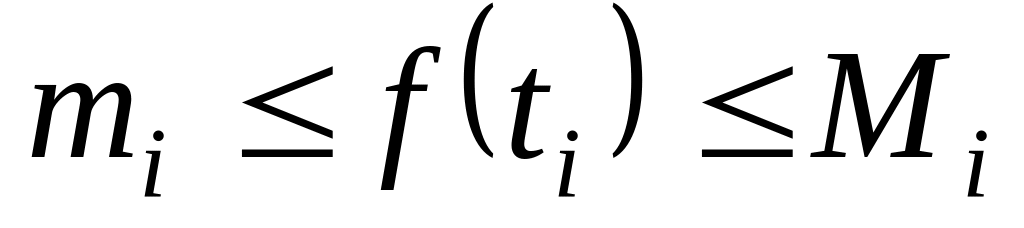 .
.Для фиксированных разбиений будет
 ,
а
,
а
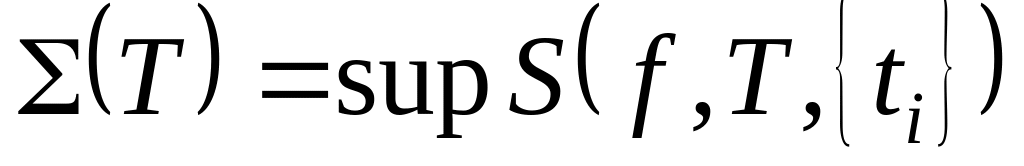 .
Рассмотрим
.
Рассмотрим
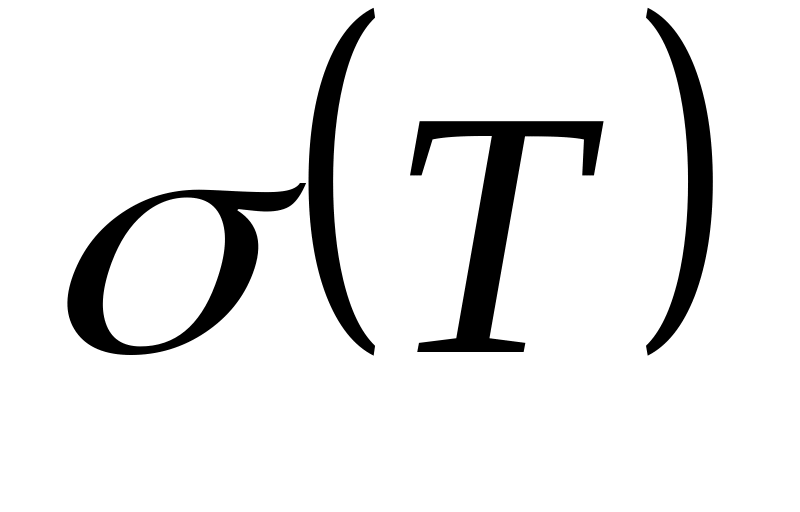 .
Возьмём
.
Т.к.
.
Возьмём
.
Т.к.
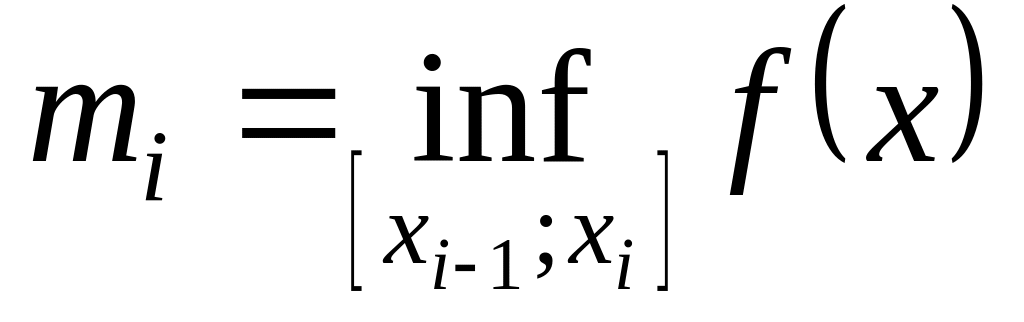 ,
то для нашего
,
то для нашего
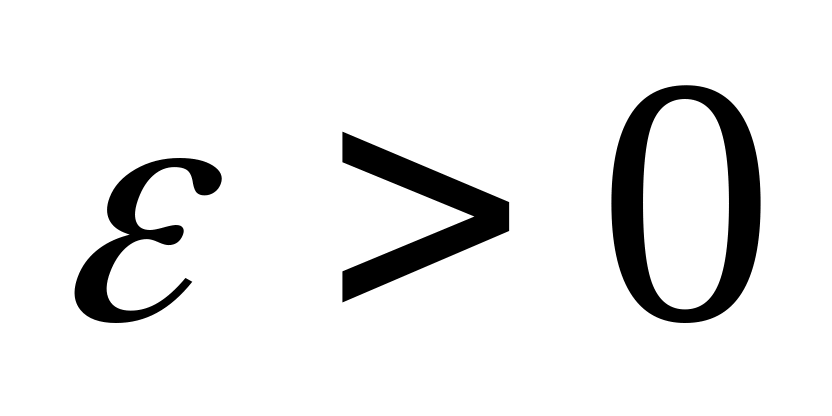

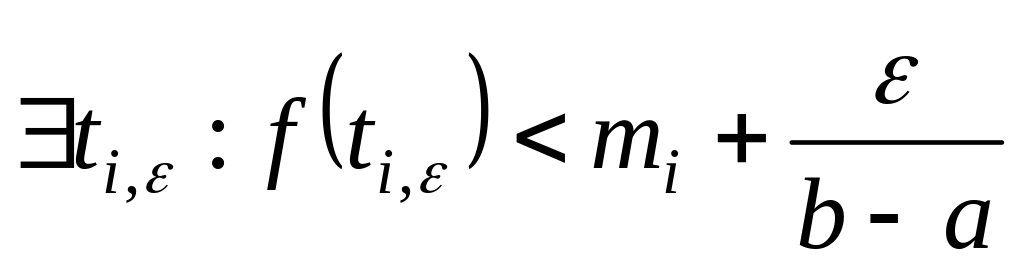 .
Тогда
.
Тогда
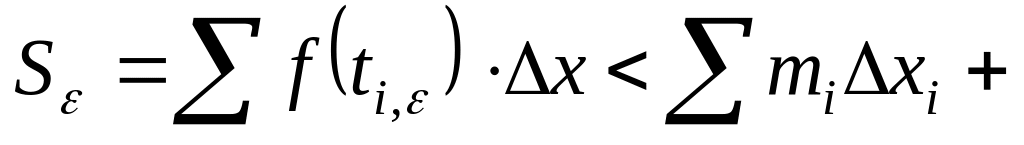
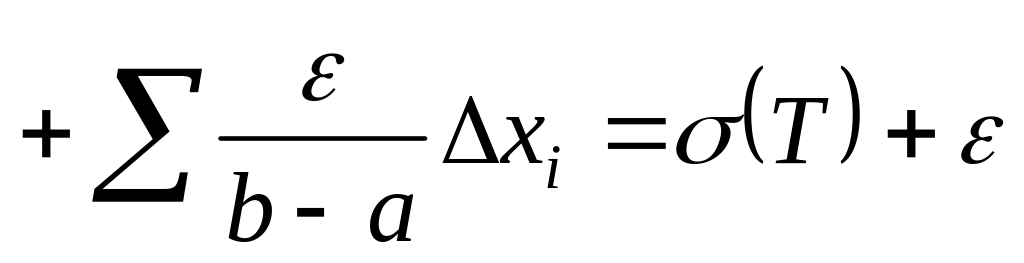 .
Т.к. кроме того, для
.
Т.к. кроме того, для
 будет
будет
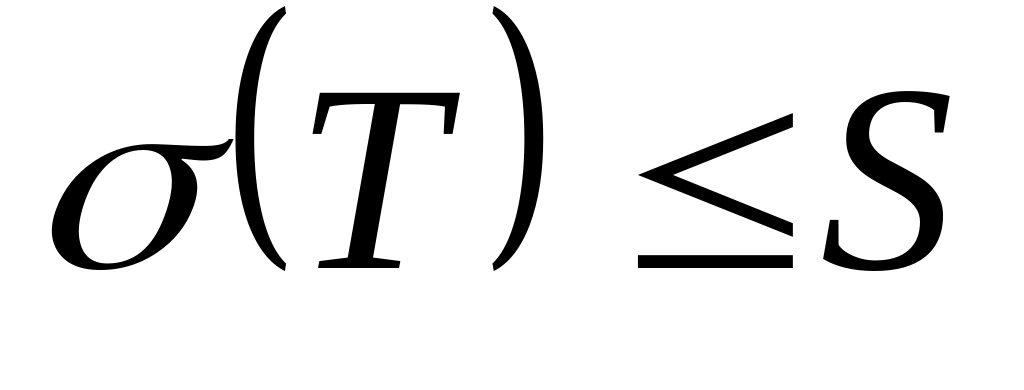 ,
то
,
то
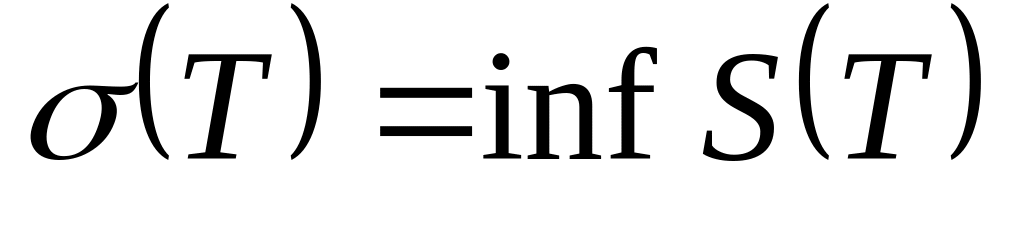 .
.При измельчении разбиения нижняя сумма Дарбу либо останется прежней, либо возрастёт, верхняя – либо останется прежней, либо уменьшится. Достаточно доказать при добавлении одной точки. Для нижней суммы.
 и
и
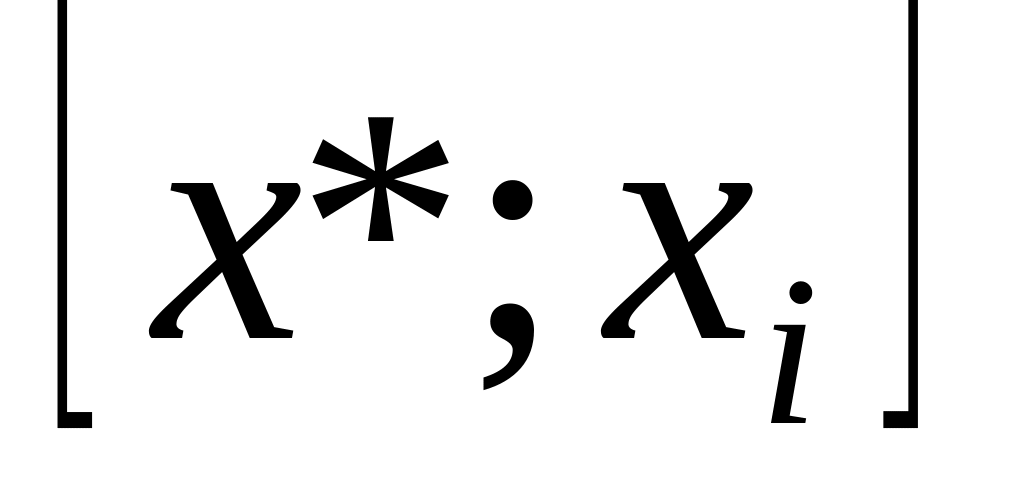 ,
,
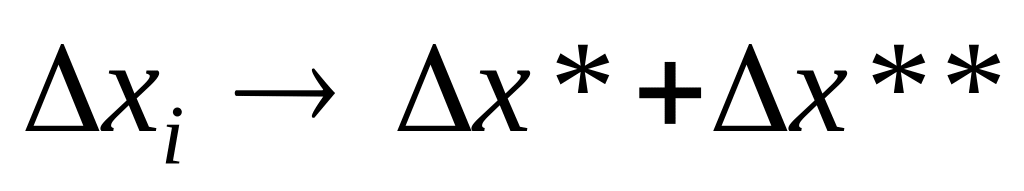 ,
,
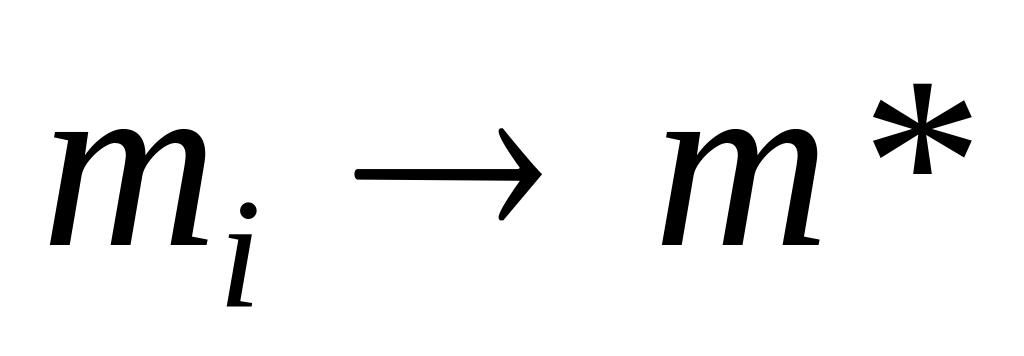 и
и
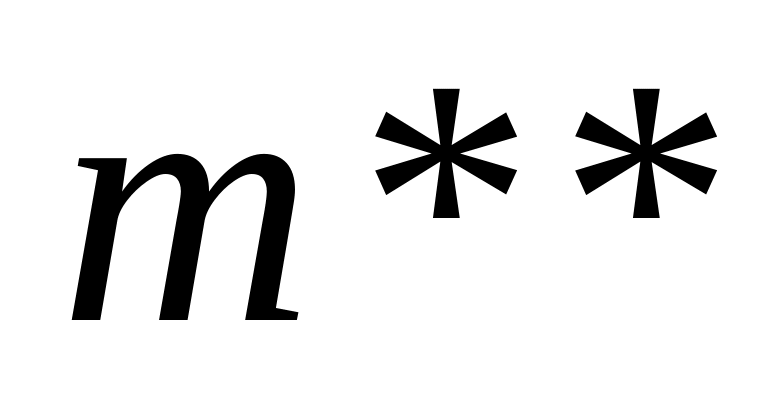 ,
где
,
где
 и
и
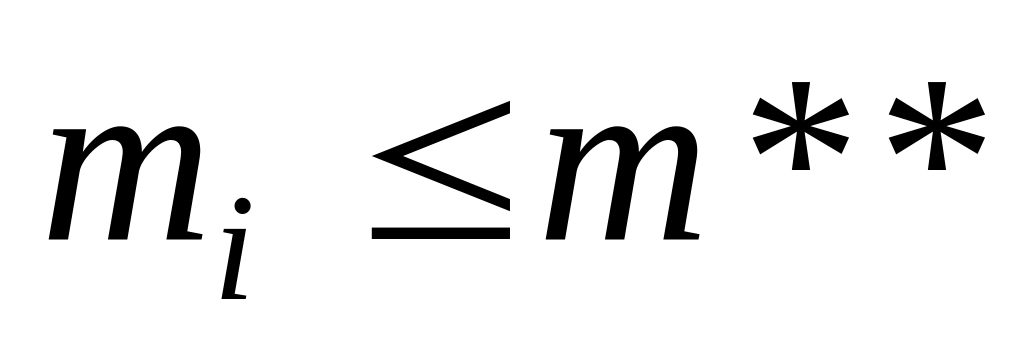 .
.
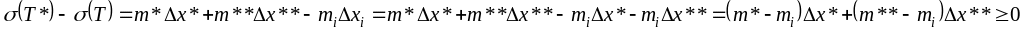 ,
т.е.
,
т.е.
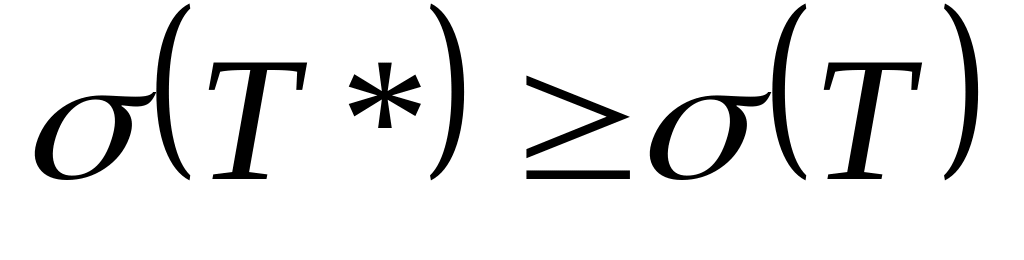 .
.Для любых двух разбиений
 и
и
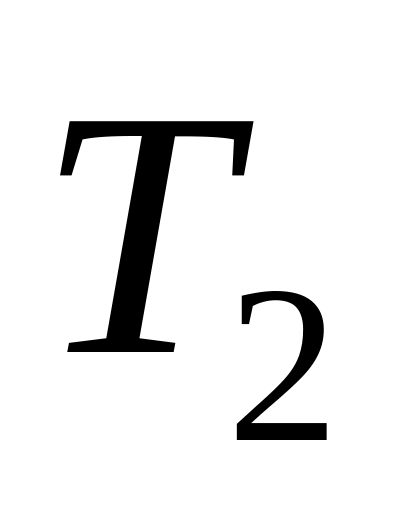 будет
будет
 .
Пусть даны разбиения
и
.
Введём
.
Пусть даны разбиения
и
.
Введём
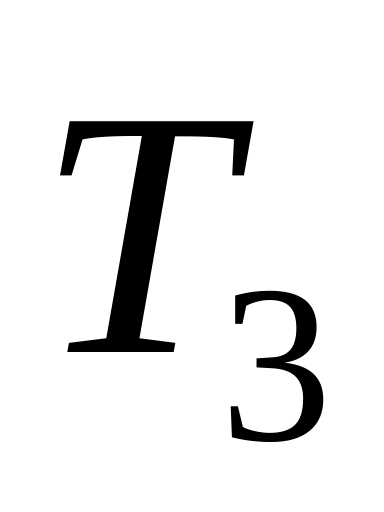 – их общее измельчение. Тогда
– их общее измельчение. Тогда
 ,
т.е.
.
,
т.е.
.
![]() – нижний интеграл Дарбу,
а
– нижний интеграл Дарбу,
а
![]() – верхний интеграл
Дарбу.
– верхний интеграл
Дарбу.
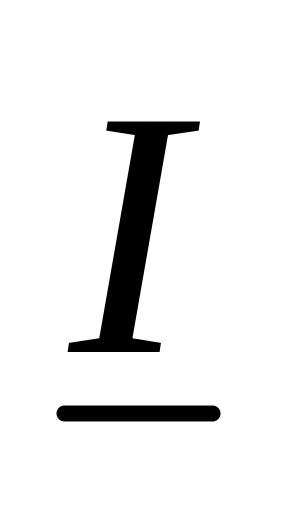 и
и
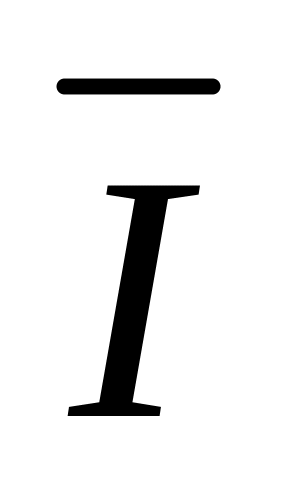 существуют. Рассмотрим
существуют. Рассмотрим
 .
Оно не пусто, т.к. содержит, например,
.
Оно не пусто, т.к. содержит, например,
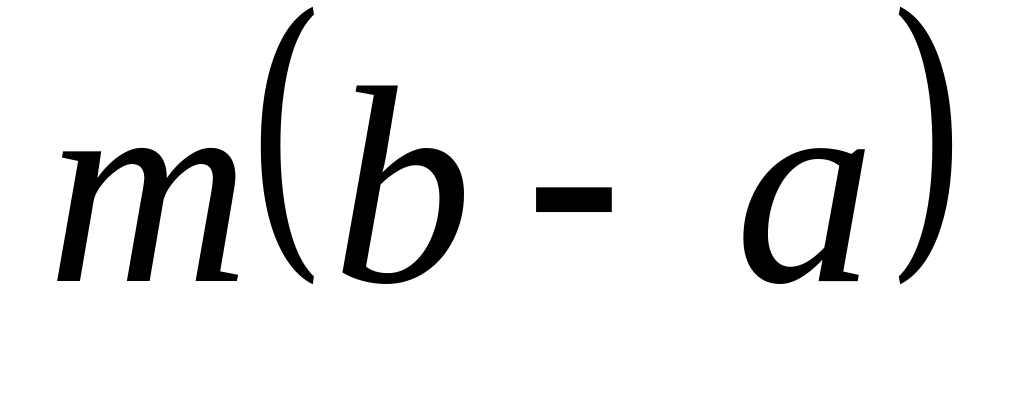 и ограничено сверху любой фиксированной
верхней суммой, например,
и ограничено сверху любой фиксированной
верхней суммой, например,
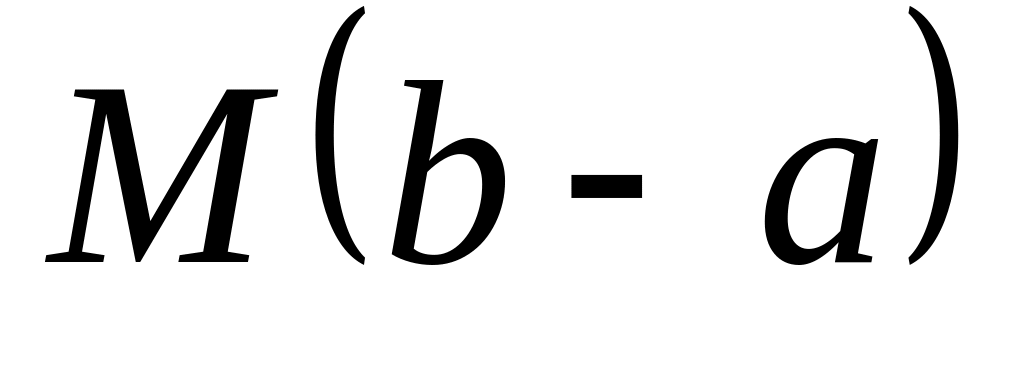 ,
следовательно
,
следовательно
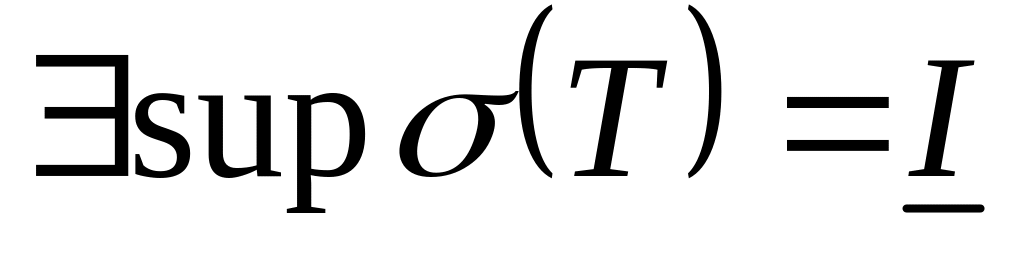 .
Для
– аналогично.
.
Для
– аналогично.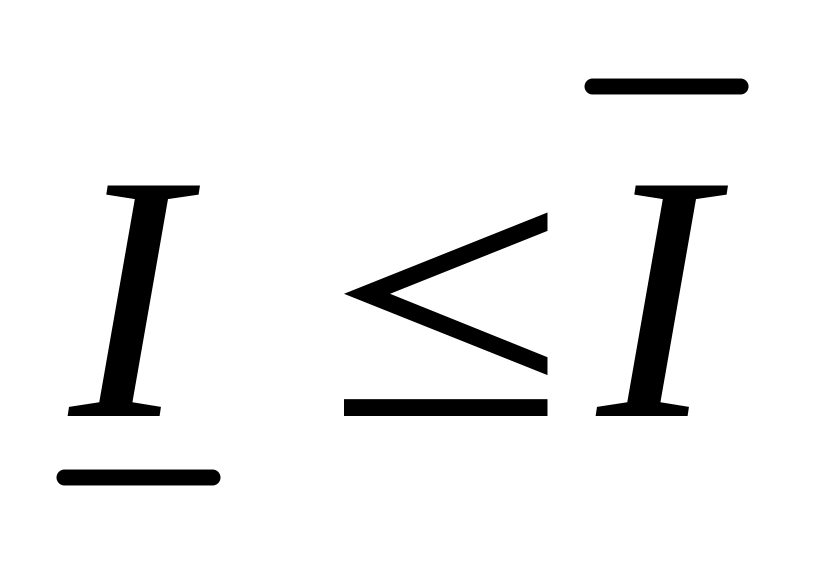 .
Предположим, что
.
Предположим, что
 .
Пусть
.
Пусть
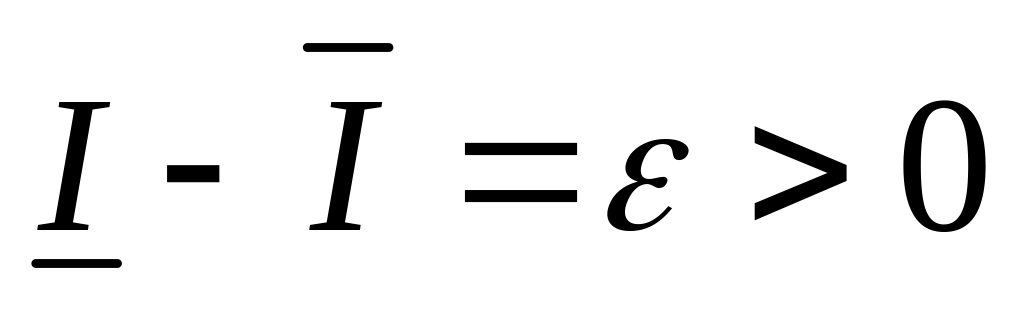 .
По определению
и
.
По определению
и
 и
и
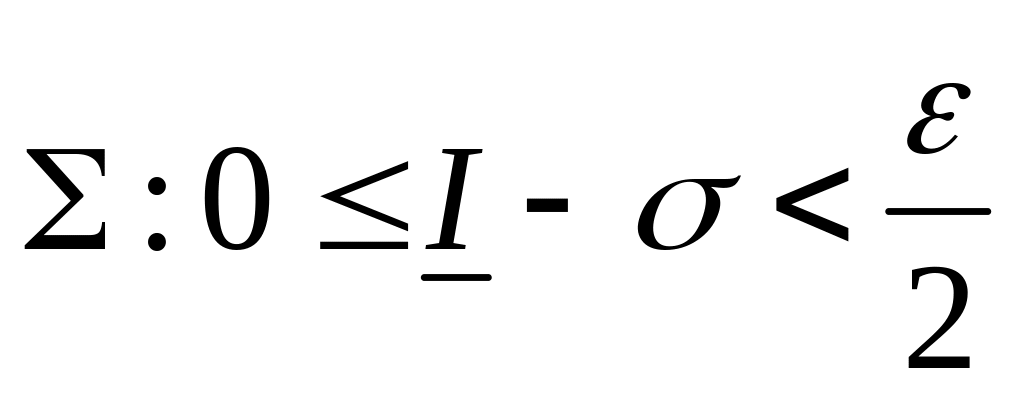 ,
,
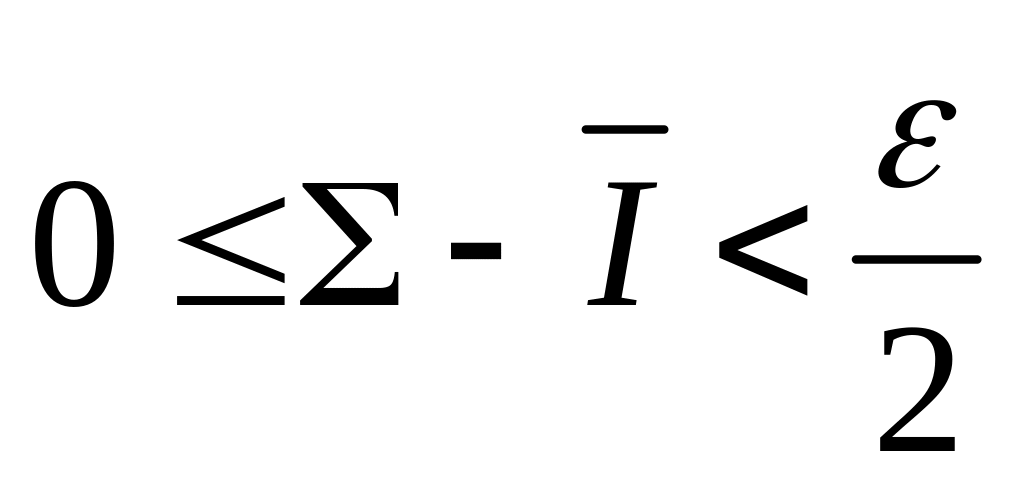 .
Сложим эти неравенства:
.
Сложим эти неравенства:
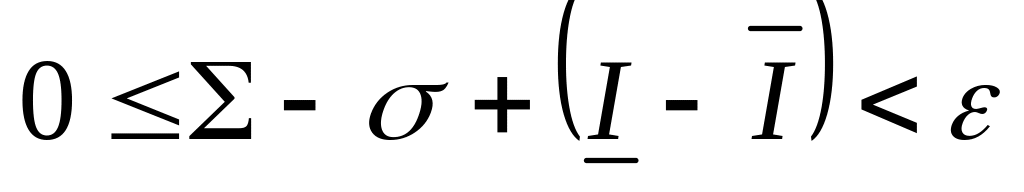 ,
т.е.
,
т.е.
 или
или
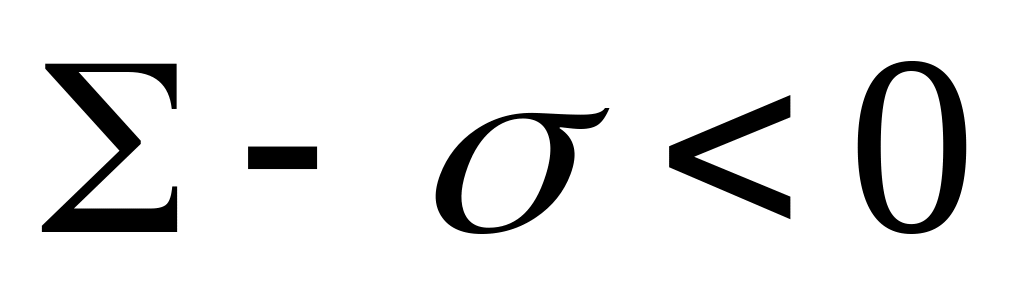 ,
т.е.
,
т.е.
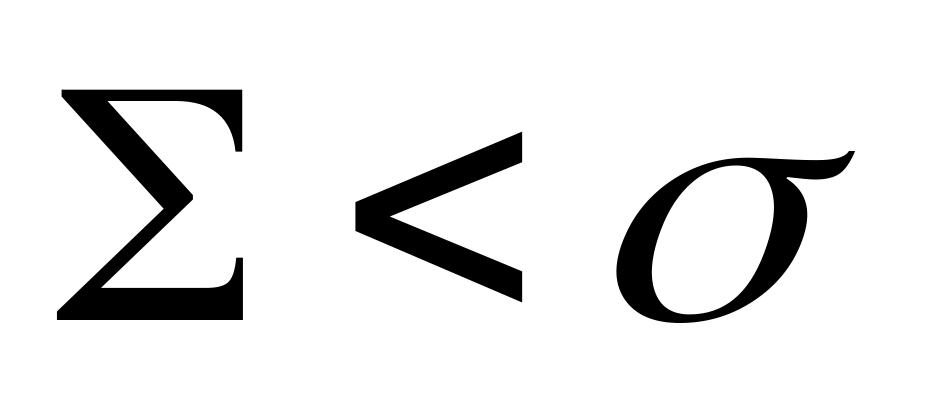 ,
чего быть не может.
,
чего быть не может.Если к разбиению T добавлено p точек и получено разбиение
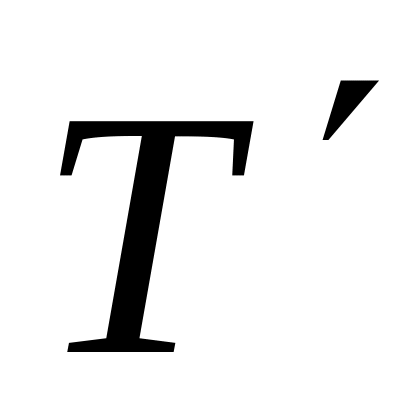 ,
причём
,
причём
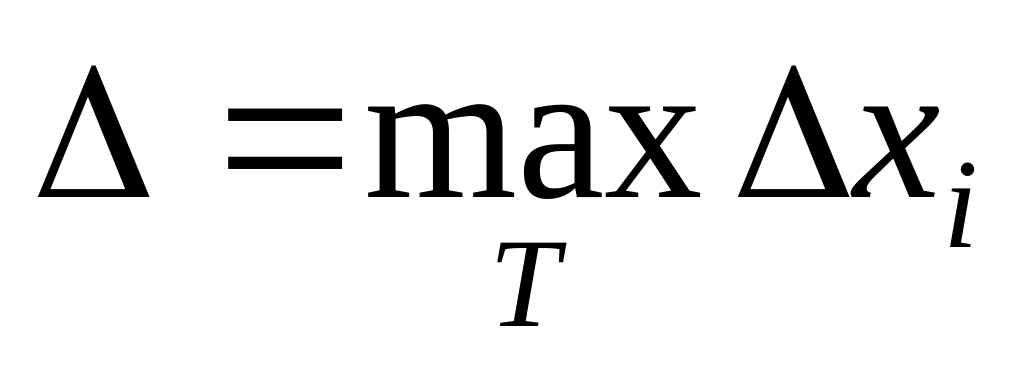 ,
то выполняются неравенства
,
то выполняются неравенства
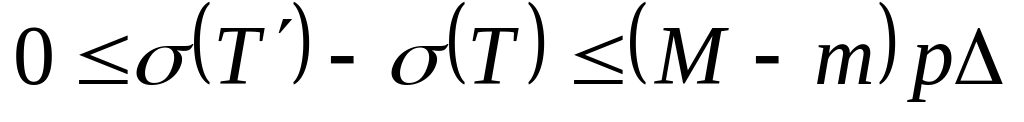 ,
,
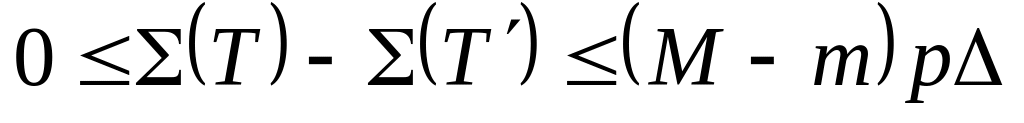 .
Достаточно рассмотреть для
.
Достаточно рассмотреть для
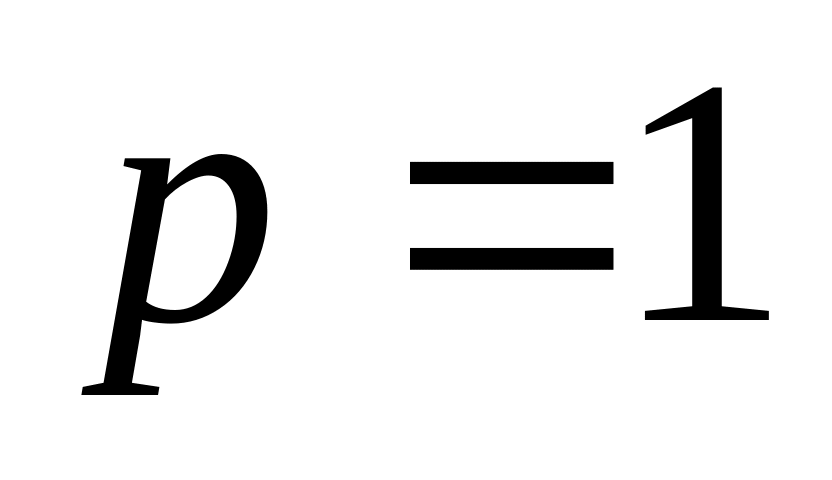 .
Добавим точку
.
Добавим точку
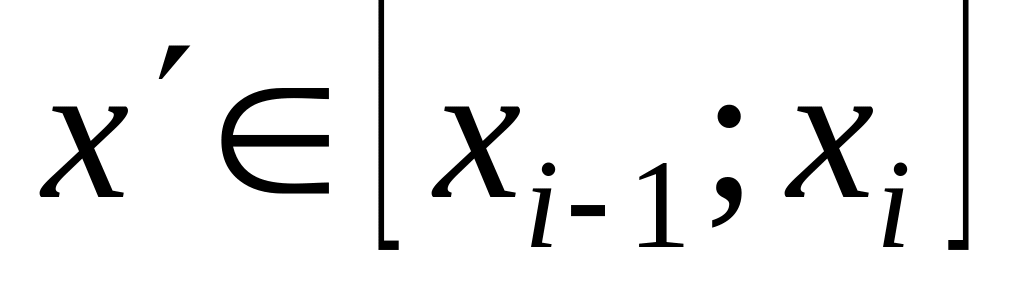 .
Тогда
.
Тогда
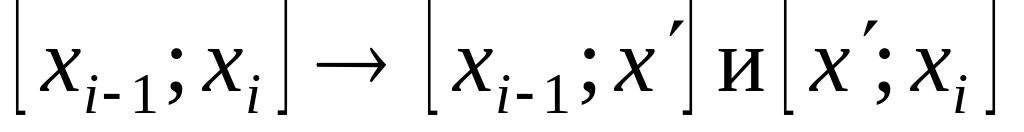 ,
,
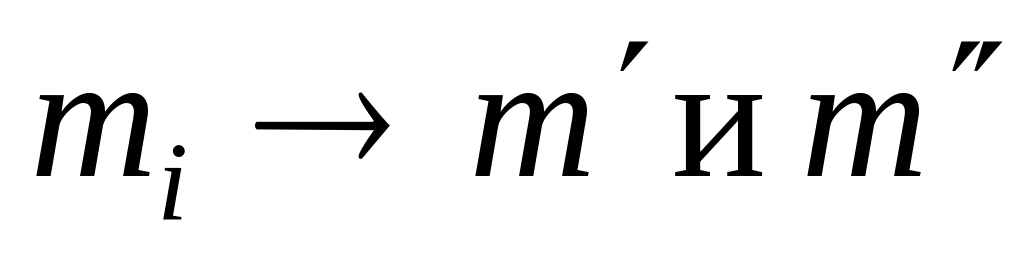 ,
,
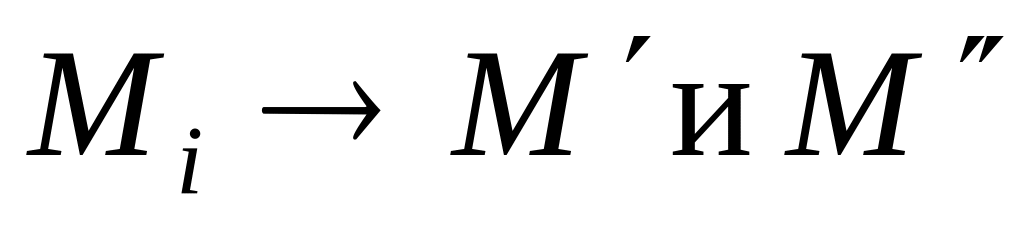 ,
,
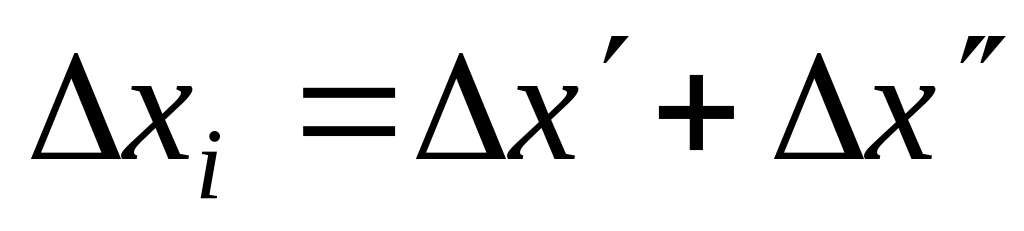 ,
,
 .
Имеем
.
Имеем
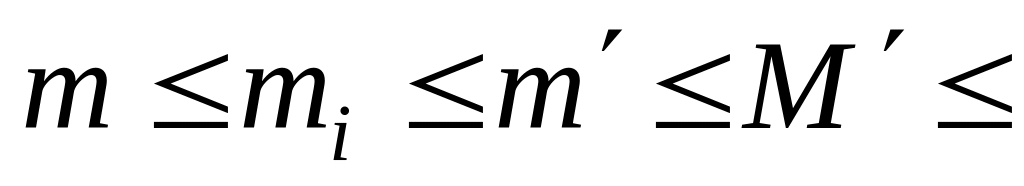
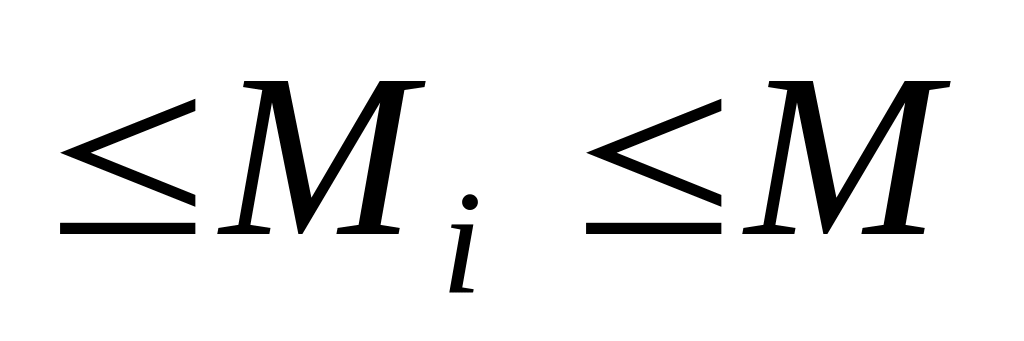 ,
,
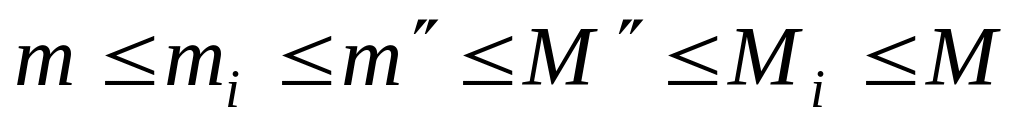 ,
откуда
,
откуда
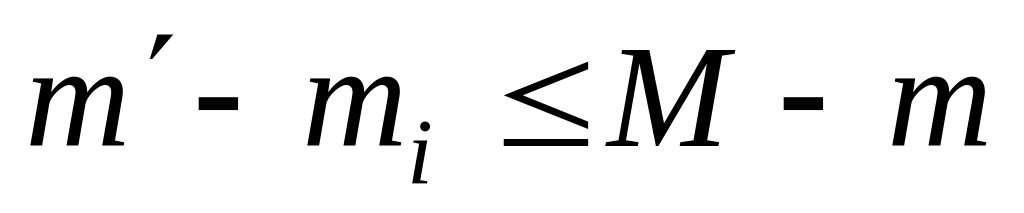 ,
,
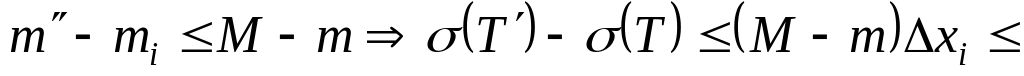
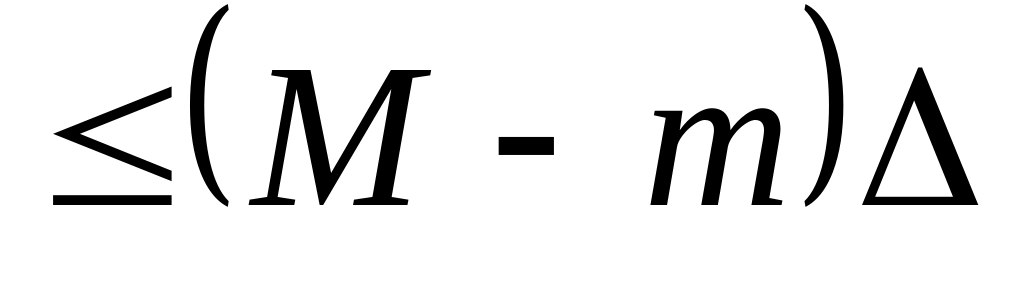 .
.Лемма Дарбу:
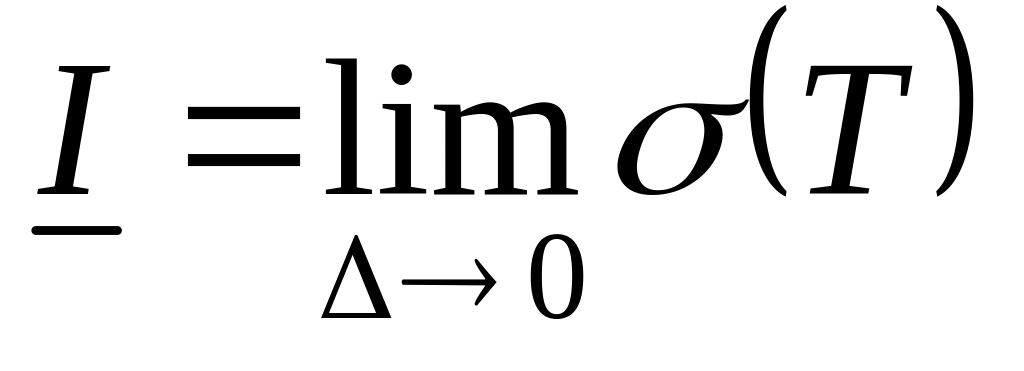 ,
,
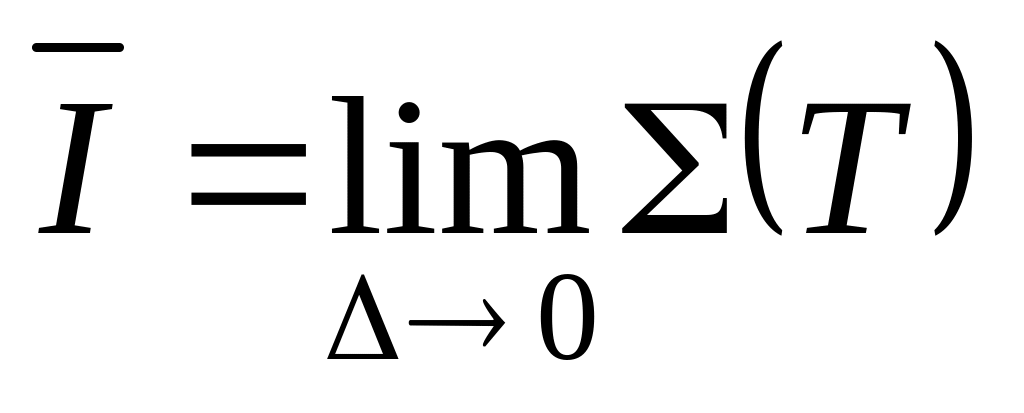 .
Достаточно рассмотреть случай,
когда
.
Достаточно рассмотреть случай,
когда
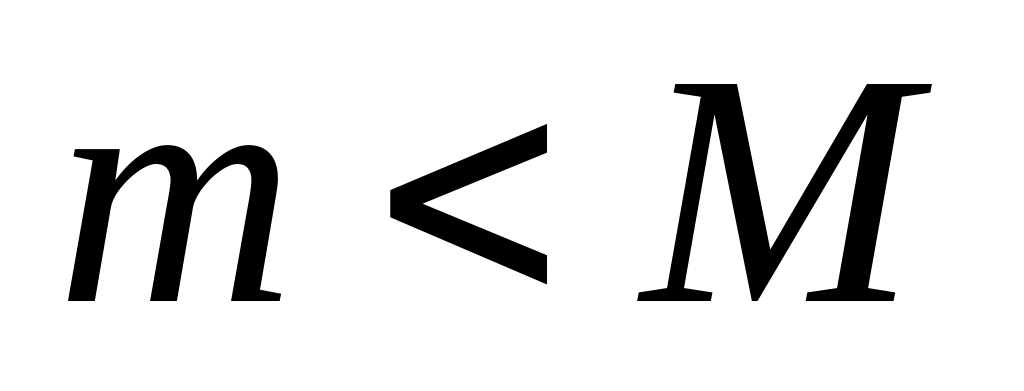 (Т.к. если
(Т.к. если
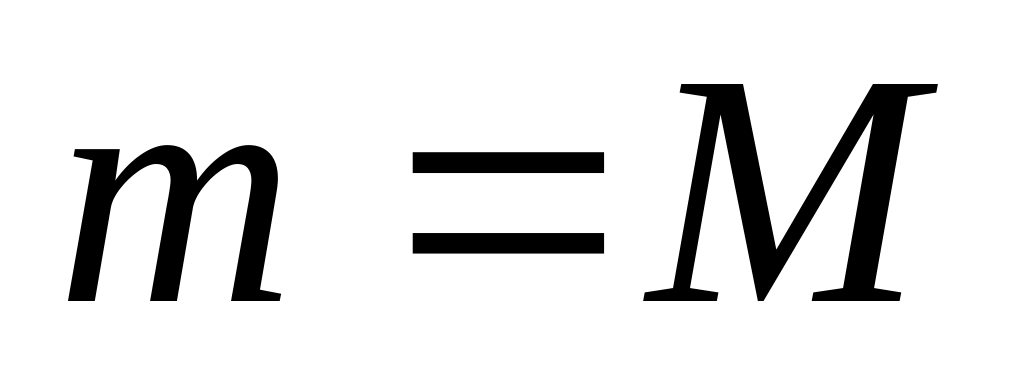 ,
то
,
то
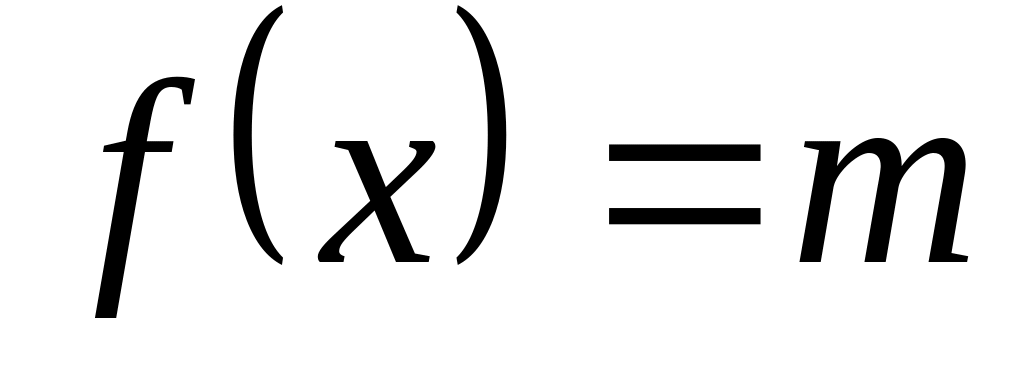 и все
и все
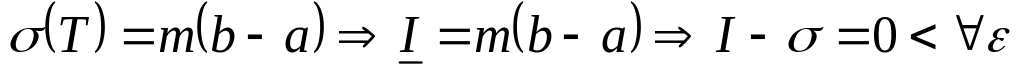 ).
Возьмём
.
Т.к.
).
Возьмём
.
Т.к.
 ,
то
,
то
 .
Пусть p – количество
точек разбиения T*,
лежащих внутри
.
Пусть p – количество
точек разбиения T*,
лежащих внутри
 .
Положим
.
Положим
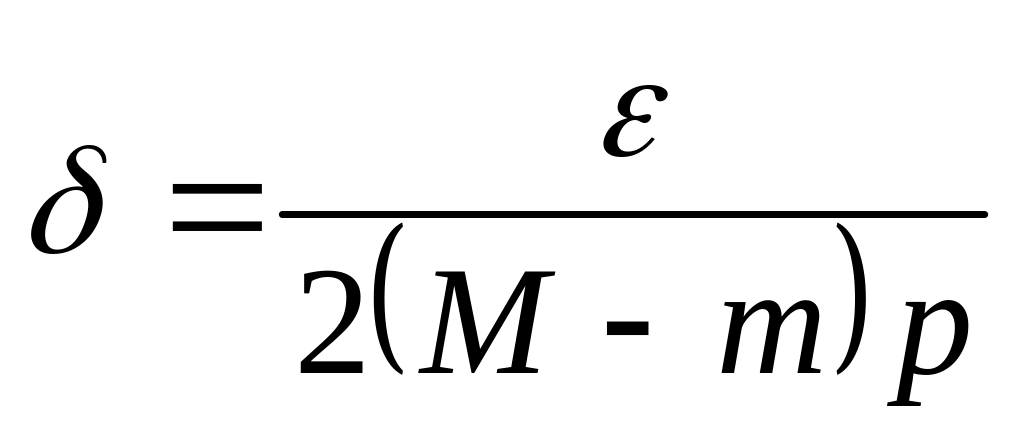 и рассмотрим произвольное разбиение
T с
и рассмотрим произвольное разбиение
T с
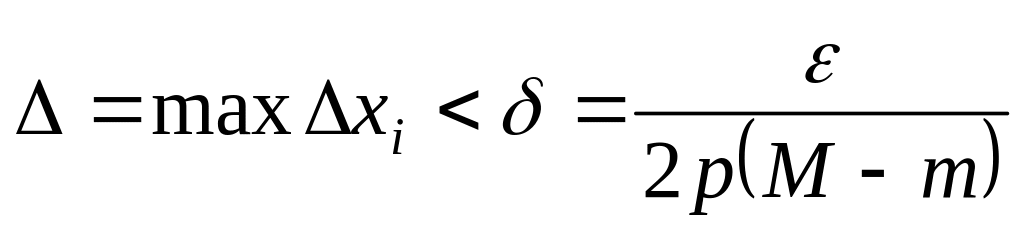 .
Добавим к Т точки T*
и получим разбиение
.
Тогда, по седьмому свойству,
.
Добавим к Т точки T*
и получим разбиение
.
Тогда, по седьмому свойству,

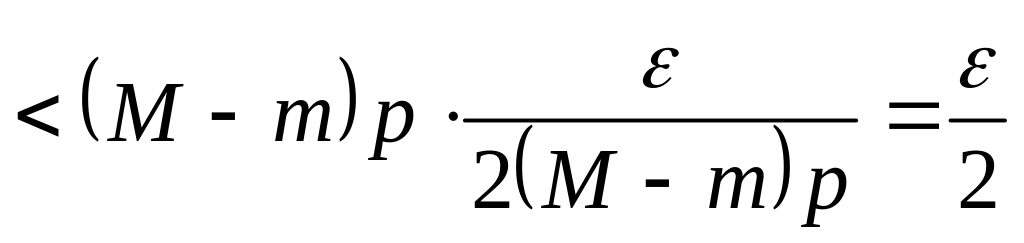 .
С другой стороны,
– измельчение T*,
поэтому
.
С другой стороны,
– измельчение T*,
поэтому
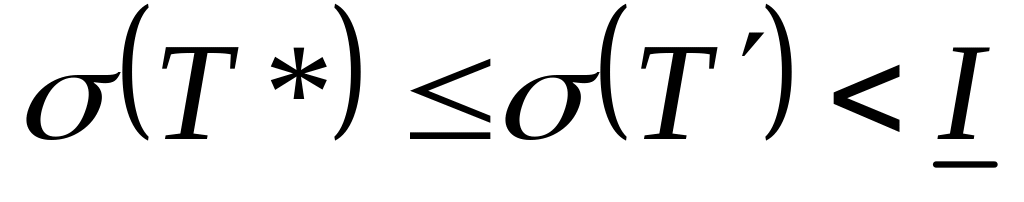 ,
откуда
,
откуда
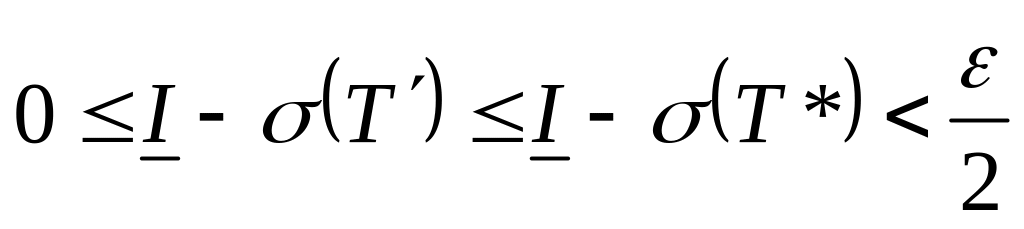 .
Итак,
.
Итак,
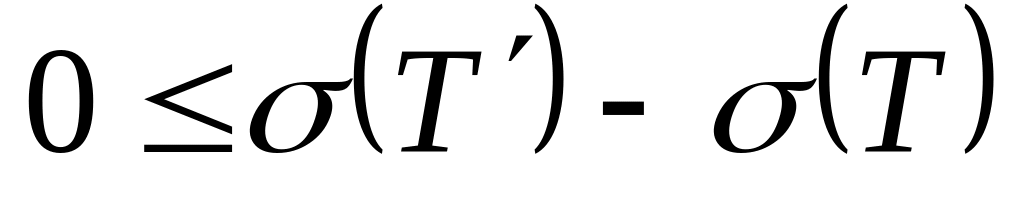 ,
,
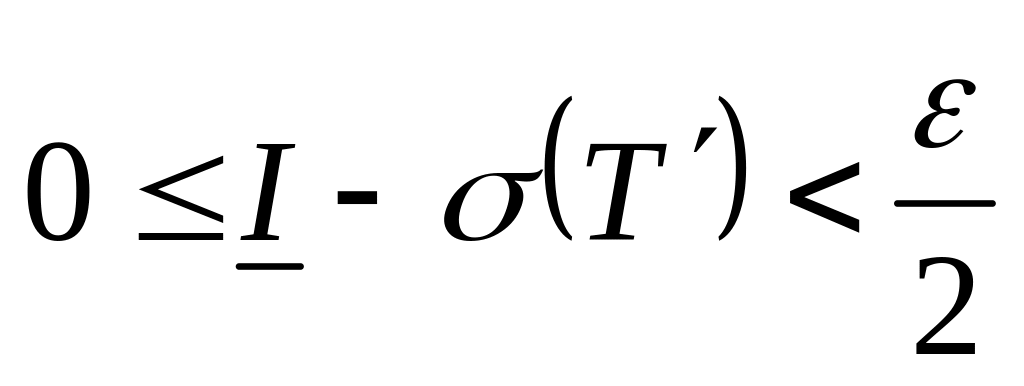 .
Сложим и получим
.
Сложим и получим
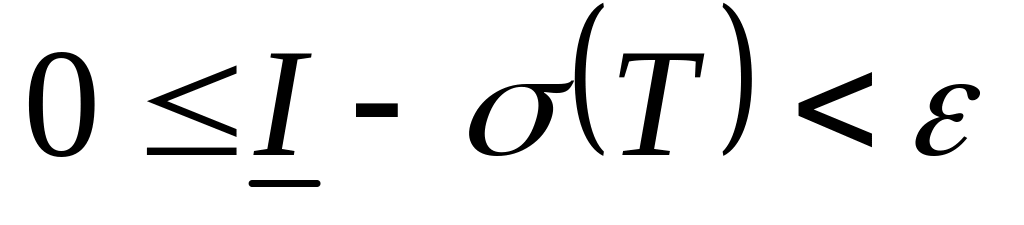 .
Т.к. T – произвольное
разбиение, то это и значит, что
.
.
Т.к. T – произвольное
разбиение, то это и значит, что
.
I формулировка
критерия интегрируемости: Для
того, чтобы ограниченная функция была
интегрируема на
,
необходимо и достаточно, чтобы для
существовало бы разбиение
![]() .
.
Пусть
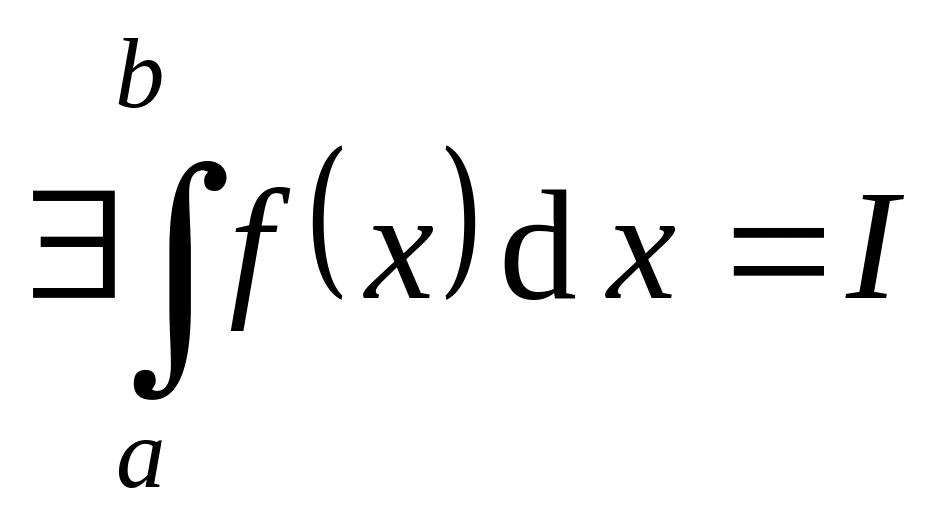 .
Возьмём
.
По определению интеграла существует
разбиение T такое,
что при любом выборе точек
.
Возьмём
.
По определению интеграла существует
разбиение T такое,
что при любом выборе точек
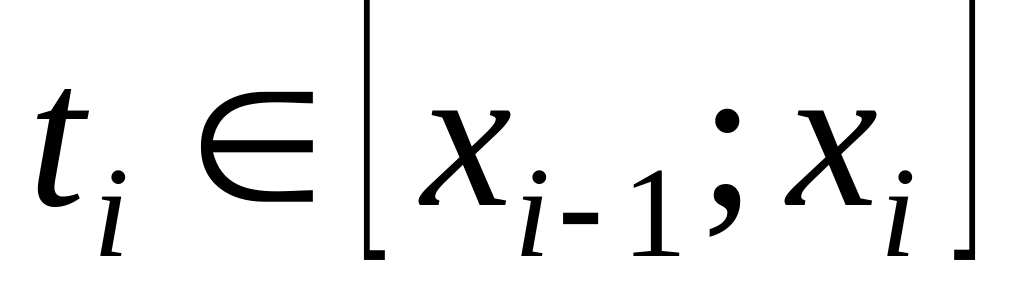 будет
будет
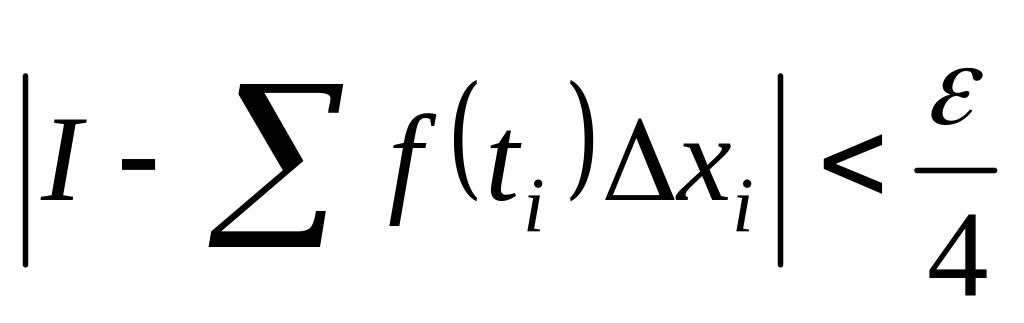 .
Т.к. для фиксированного T
будет
.
Т.к. для фиксированного T
будет
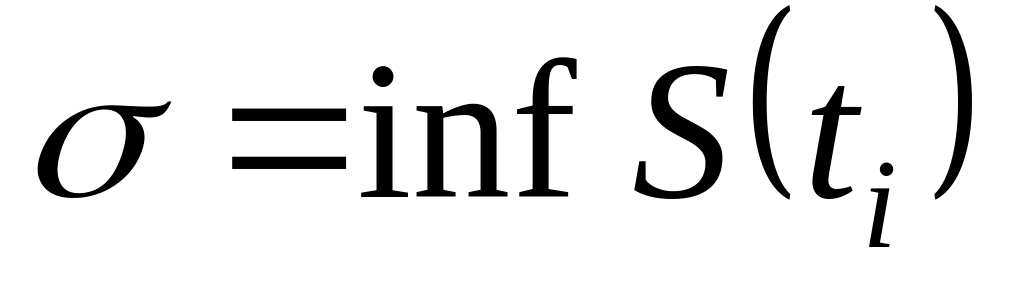 ,
,
 ,
то для того же
,
то для того же
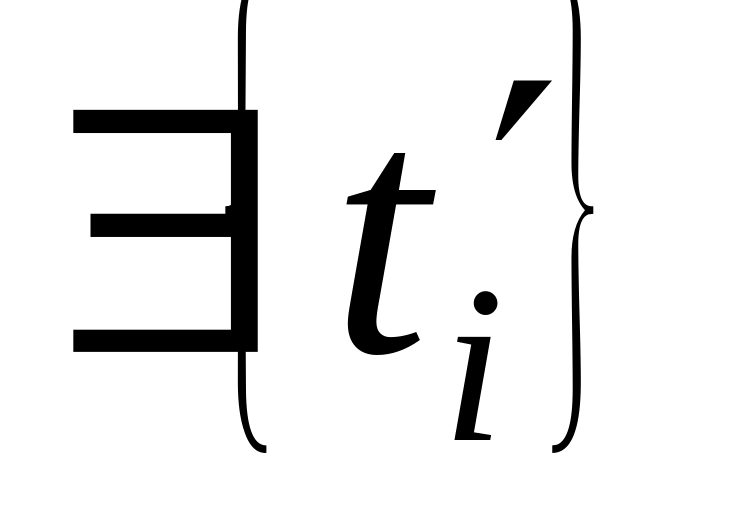 и
и
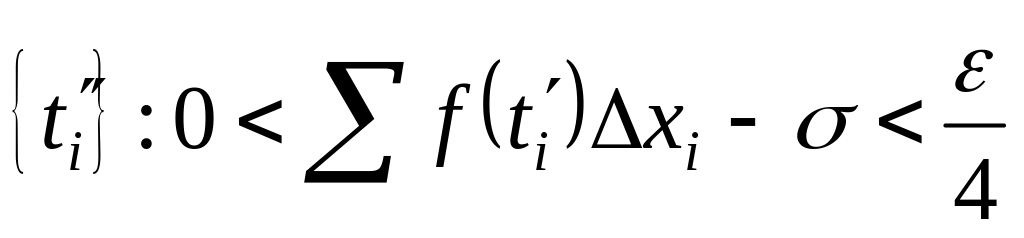 ,
,
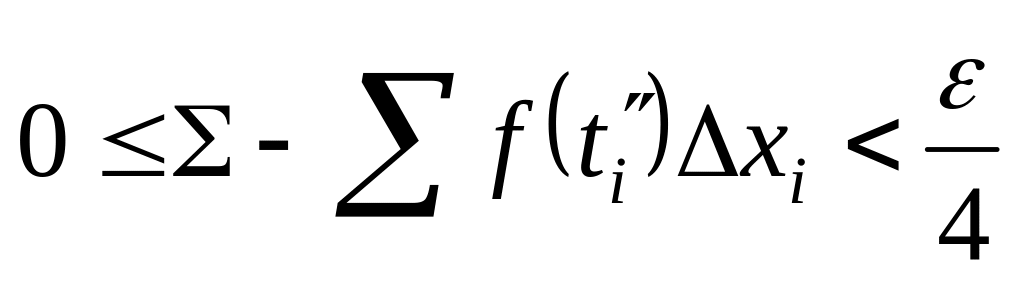 .
Отсюда
.
Отсюда
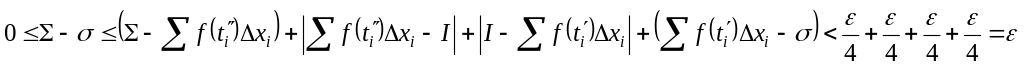 .
.Пусть для
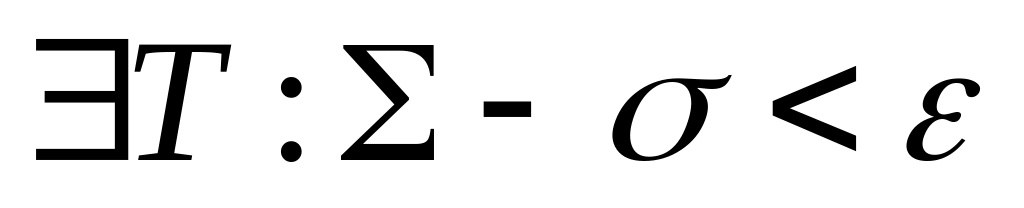 .
Т.к.
.
Т.к.
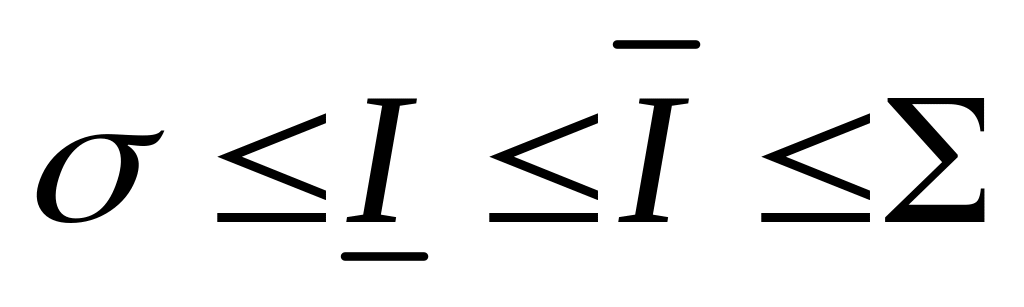 ,
то для
будет
,
то для
будет
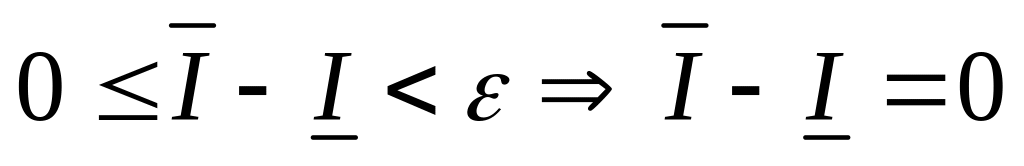 ,
т.е.
,
т.е.
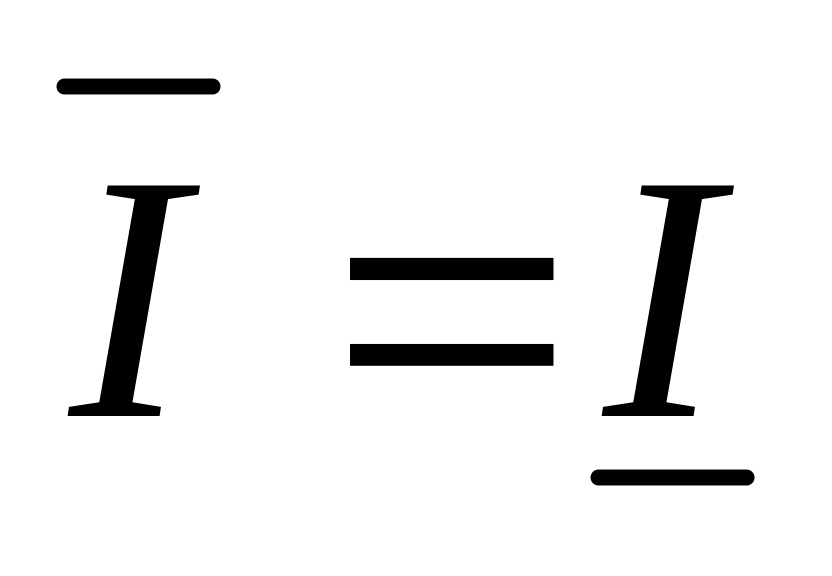 .
Обозначим
.
Обозначим
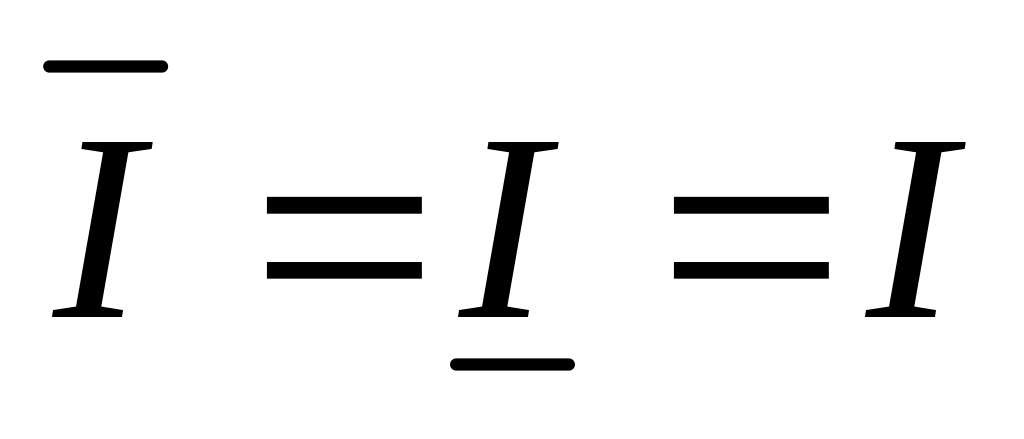 и докажем, что
и докажем, что
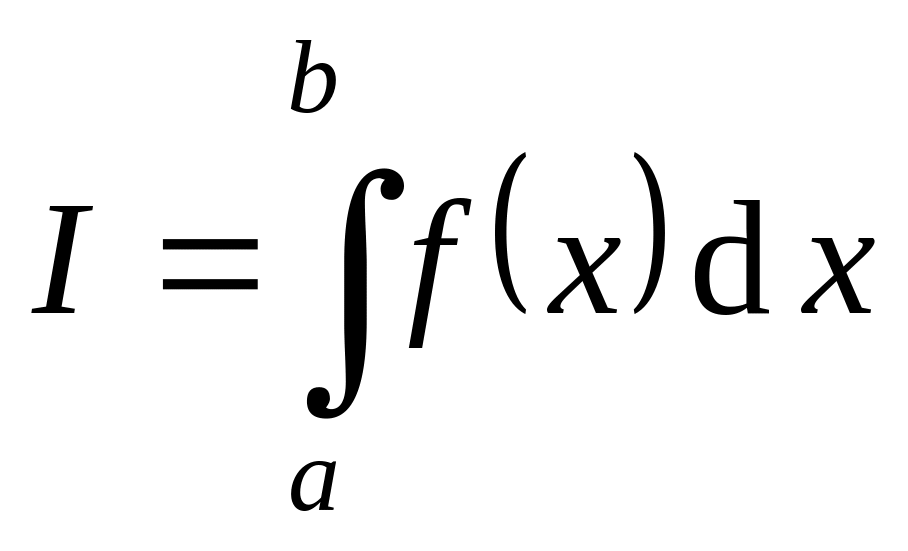 .
Т.к.
.
Т.к.
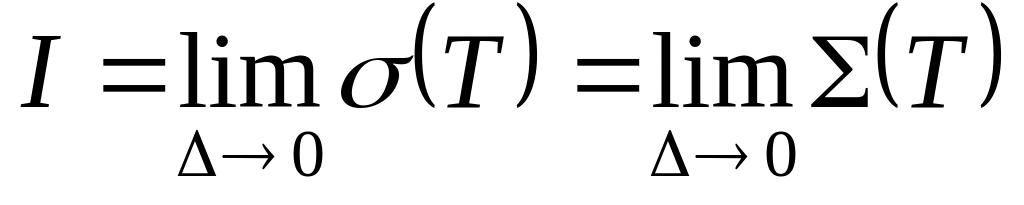 ,
то для
для
,
то для
для
 будет
будет
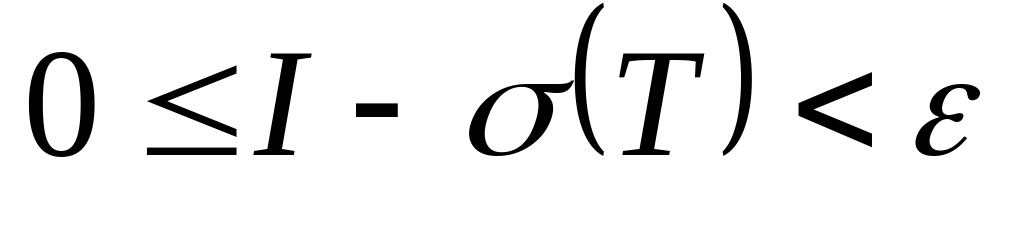 ,
,
 ,
а т.к. при
,
а т.к. при
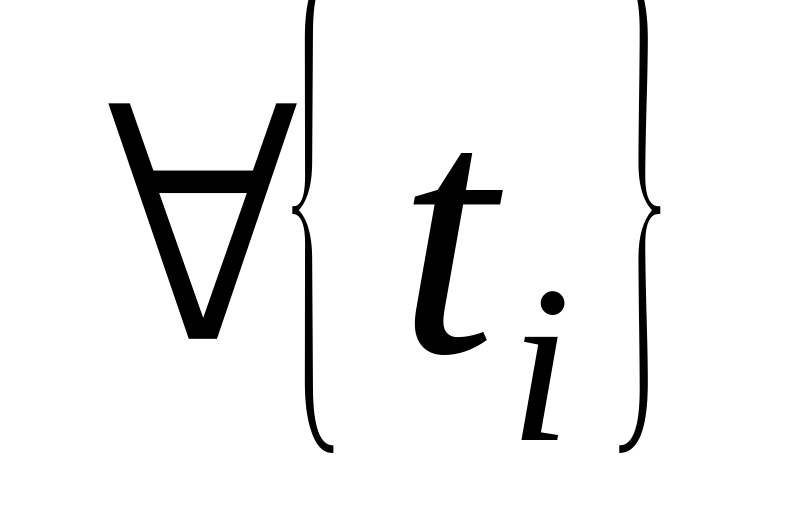 будет
будет
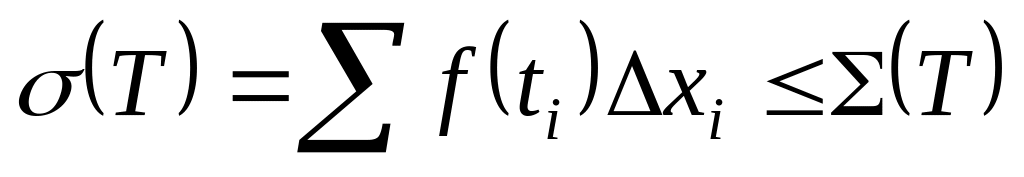 ,
то для
при
будет
,
то для
при
будет
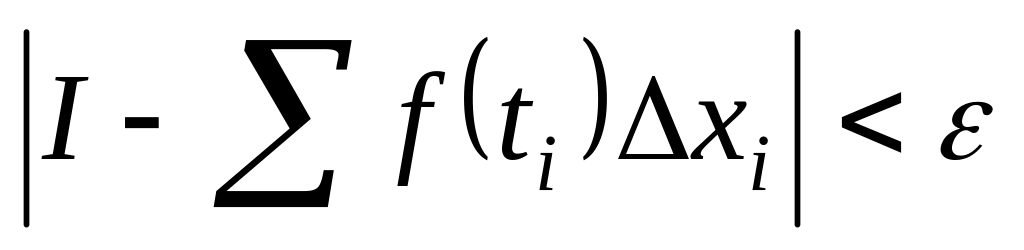 ,
т.е.
.
,
т.е.
.
Если
![]() ,
то
называется интегрируемой
по Дарбу и I
– интеграл по Дарбу.
,
то
называется интегрируемой
по Дарбу и I
– интеграл по Дарбу.
Понятия интеграла Римана
и интеграла Дарбу совпадают:
![]() .
.
В критерии достаточно
существование
и
![]() .
.
Т.к.
![]() ,
то
,
то
![]() .
.
II формулировка
критерия интегрируемости: Для
интегрируемости
,
ограниченной на
,
необходимо и достаточно, чтобы для
существовало разбиение T
такое, что
![]() .
.
