Оценки интегралов

Если и интегрируема на и , то .

Т.к. , то и .

Если и обе функции интегрируемы на , то .

, т.к. .

Если интегрируема на , то .

Пусть, например, . Т.к. , то , т.е. .

I теорема о среднем: Пусть интегрируема на и . Тогда и . Если же непрерывна на , то .

Пусть, например, . Т.к. , то , т.е. 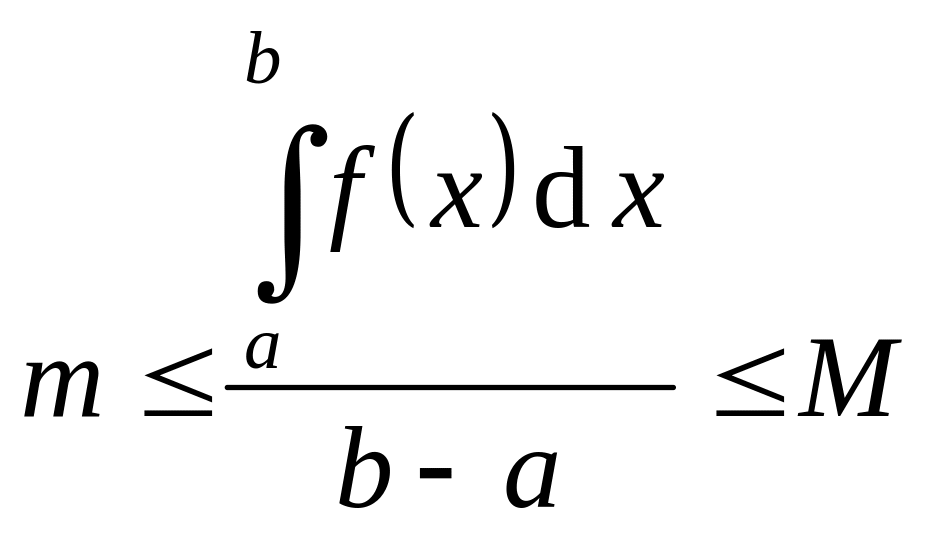. Обозначим . Тогда и . Если непрерывна на , то положим , . Т.к. , то .

Обобщённая I теорема о среднем: Пусть и интегрируемы на , сохраняет знак на и . Тогда и . Если, кроме того, непрерывна на , то .

Пусть, например, . Тогда при , откуда . Если , то , т.е. при будет . Если же , то . Положив , получим . Для непрерывной – как в предыдущей теореме.

Пусть непрерывна на , , и на всём . Тогда .

По условию . Т.к. непрерывна на , то найдётся на будет (естественно, выбираем  так, чтобы ). Тогда .

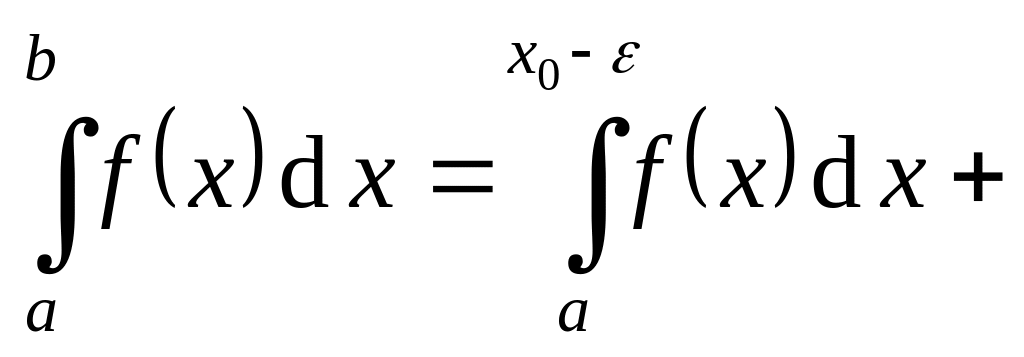
Пусть интегрируема на , а только в конечном числе точек . Тогда тоже интегрируема на и .

Имеем при . Но тогда отличается от не более чем в слагаемых, которые стремятся к 0 при , т.е. интегрируема на . Тогда , т.к. при вычислении предела можно брать для .

Интеграл как функция верхнего предела

Пусть интегрируема на . Тогда для – интеграл с верхним пределом.

Если интегрируема на , то непрерывна.

Возьмём и и рассмотрим . Имеем (по I теореме о среднем) , где . Отсюда при будет и, следовательно, при непрерывна на .

Если непрерывна на , то дифференцируема на , причём для , т.е. – первообразная для на .

Имеем для и будет (по I теореме о среднем для непрерывной функции) , где . Т.к. непрерывна на , то при будет , т.е. существует .

Формула Ньютона-Лейбница: Если непрерывна на и – какая-то первообразная для на , то .

Заметим вначале, что первообразные у существуют. Например, . Т.к. две первообразные на одном множестве отличаются на постоянную, то . Отсюда и, значит, . В частности, .

Если на заданы и , причём и непрерывны на (тогда и тем более непрерывны на ), то .

Заметим, что – первообразная для , т.к. . Т.к. непрерывна на , то к ней применима формула Ньютона-Лейбница: .

Пусть

1. непрерывна на .

2. – функция такая, что значения заполняют , когда 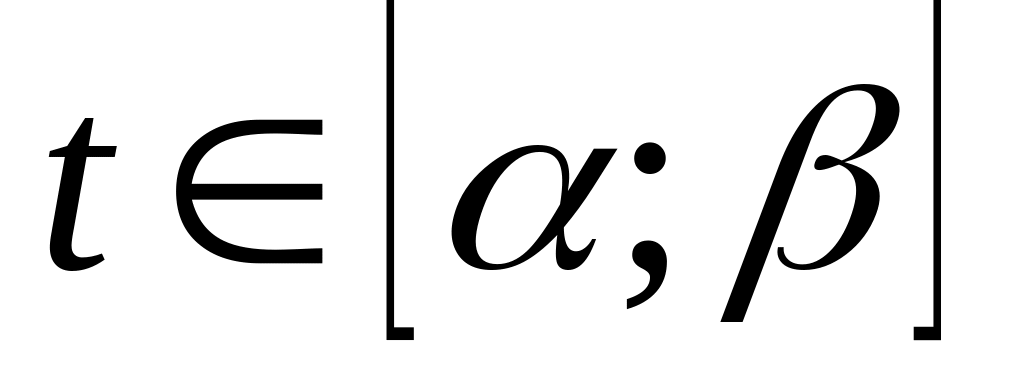, причём непрерывна на (тогда и непрерывна на ).

3. .

Тогда .

Пусть – первообразная для на . Тогда – первообразная для на , т.к. . Т.к. на и на непрерывны, то применима формула Ньютона-Лейбница: , .

Пусть интегрируема на и – такая функция, что непрерывна на , всюду на или всюду, исключая конечное число точек. Тогда .

Разобьем точками так, что все точки, в которых не попадают в число точек разбиения. Тогда (по т. Лагранжа для каждого ) (где ) . Т.к. интегрируема на , то при любых разбиениях T с при любом выборе , где , т.е., в частности, при нашем разбиении и нашем выборе . Но при таком разбиении и выборе .