Ряды со знакопеременными членами

Ряд , где называется знакопеременным рядом.

Признак Лейбница: Пусть не возрастает, при . Тогда сходится.

1. Рассмотрим . Имеем , т.е. не убывает. Далее, , т.е. ограничена сверху. Следовательно, существует конечный .

2. Т.к. и , то 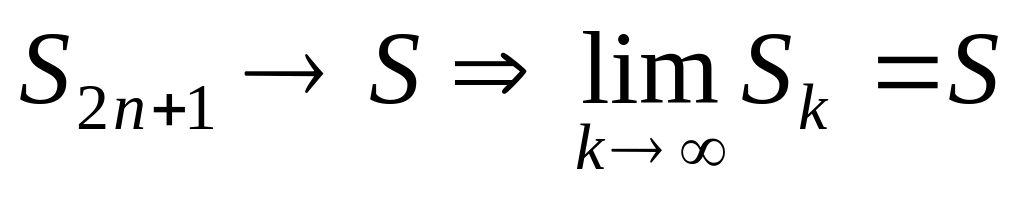, т.е. сходится.

Если , где , то .

Заметим, что , т.е. . Следовательно, или для . Т.е. при , откуда видно, что .

Признак Дирихле: Если

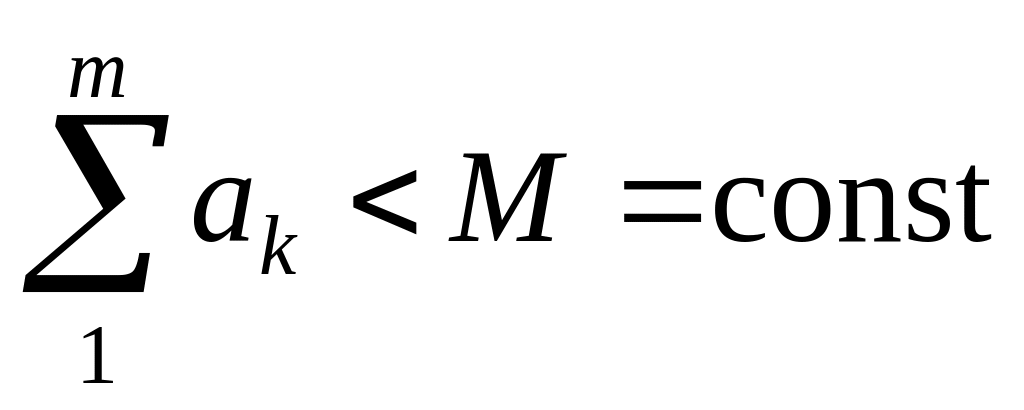1. для ,

2. монотонна,

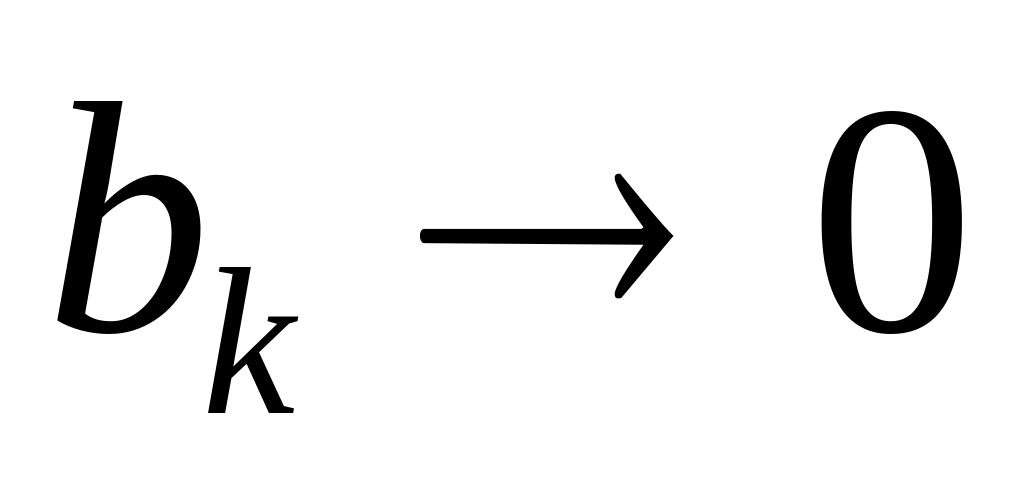3. при ,

то сходится.

Обозначим и оценим (пусть, например, ) (т.к. и , то ). Теперь возьмём . Т.к. при , то для будет . Тогда для и натуральных будет . Отсюда по критерию Коши сходится.

Признак Абеля: Пусть

1. сходится.

2. монотонна и ограничена.

Тогда сходится.

Т.к. монотонна и ограничена, то существует конечный , т.е. при , к тому же, т.к. сходится, то ограничены. Наконец, имеем – сходится, т.к. сходится по условию, а сходится по признаку Дирихле.

Действия над рядами

Лемма: Пусть сходится: и – некоторая перестановка . Тогда тоже сходится и .

Т.к. и , то . Заметим, что и рассмотрим . Тогда , где , т.е. ограничена сверху, следовательно, сходится: . Т.к. все , то и . Повторяя все эти рассуждения для и считая его перестановкой , получим, что .

Если сходится абсолютно и – любая перестановка , то сходится абсолютно, причём .

1. Абсолютная сходимость следует из применения леммы к рядам и .

2. Обозначим – положительные члены , взятые в их прежнем порядке, – модули отрицательных членов , взятые в их прежнем порядке. Заметим, что , где таково, что в находятся все . Но сходится, следовательно, для m и, значит, , откуда следует, что сходится: . Аналогично для – он сходится и равен Q. Теперь рассмотрим при , т.к. при этом и , следовательно, . Теперь рассмотрим . Т.к. и – перестановка и , то они сходятся к тем же суммам: , а, значит, , т.е. .

Для абсолютно сходящегося ряда . Очевидно, что для неабсолютно сходящегося и .

Теорема Римана: Если неабсолютно (условно) сходится, то для можно так переставить члены , что полученный ряд будет сходиться к A.

Пусть и абсолютно сходятся. Тогда ряд , составленный из всех попарных произведений членов рядов и , тоже абсолютно сходится, причём .

Рассмотрим , где . Т.к. и ограничены, то для n и m тоже ограничена, следовательно, сходится, т.е. сходится абсолютно. Значит, при перестановке его членов сумма его не меняется, следовательно, для вычисления её достаточно взять какую-то конкретную перестановку и посчитать предел подпоследовательности частичных сумм. Например: . Тогда, если обозначить , , то .

Часто располагают .

Функциональные ряды и последовательности

Пусть на множестве E задана последовательность функций . Говорят, что на E по точкам, если для , т.е. для и для будет .

Пусть на множестве E задана последовательность функций . Говорят, что (равномерно сходится к на E), если для для будет сразу для .

Обозначим . Тогда на E тогда и только тогда, когда при .

1. Пусть при , т.е. для для будет сразу для , т.е. .

2. Пусть на E. Возьмём . Тогда при и сразу при будет , откуда , что равносильно тому, что лежат в -полоске вокруг .

Пусть на множестве E задан ряд . Говорят, что равномерно сходится к сумме на E , если , т.е. для для будет сразу для .

Простейшие свойства:

1. Если , то . (Следует из того, что для ­ и )

2. Если и , то .

Возьмём . Тогда для и будет . Тогда для и будет , т.е. .

Очевидно, что эти свойства справедливы и для рядов.