
- •II семестр – весенний семестр 2003 года
- •Необходимое и достаточное условия интегрируемости
- •Классы интегрируемых функций
- •Интегралы как функции множества
- •Оценки интегралов
- •Интеграл как функция верхнего предела
- •Приложение определённого интеграла
- •Площади фигур
- •Условная сходимость
- •Ряды со знакопеременными членами
- •Действия над рядами
- •Функциональные ряды и последовательности
- •Признаки равномерной сходимости
- •Степенные ряды
- •Понятие о рядах Фурье
- •Функции нескольких переменных
- •Последовательности точек
- •Дифференцирование функций нескольких переменных
- •Производные и дифференциалы высших порядков
- •Зависимость функций
Условная сходимость
Говорят, что сходится условно, если сходится, а расходится.
Пример:
![]() .
.
Специальный признак сходимости:
Пусть на
![]() и
и
![]() непрерывны,
непрерывны,
![]() интегрируема на каждом
интегрируема на каждом
![]() и пусть
– какая-то первообразная для
и пусть
– какая-то первообразная для
![]() .
Если существует конечный
.
Если существует конечный
![]() и сходится
и сходится
![]() ,
то сходится и
,
то сходится и
![]() .
.
По формуле интегрирования по частям
![]()
![]() имеет конечный предел при
имеет конечный предел при
![]() сходится.
сходится.
Условия специального
признака выполнены, если
и
непрерывны на
![]() ,
интегрируема на
,
интегрируема на
![]() и выполнены условия:
и выполнены условия:
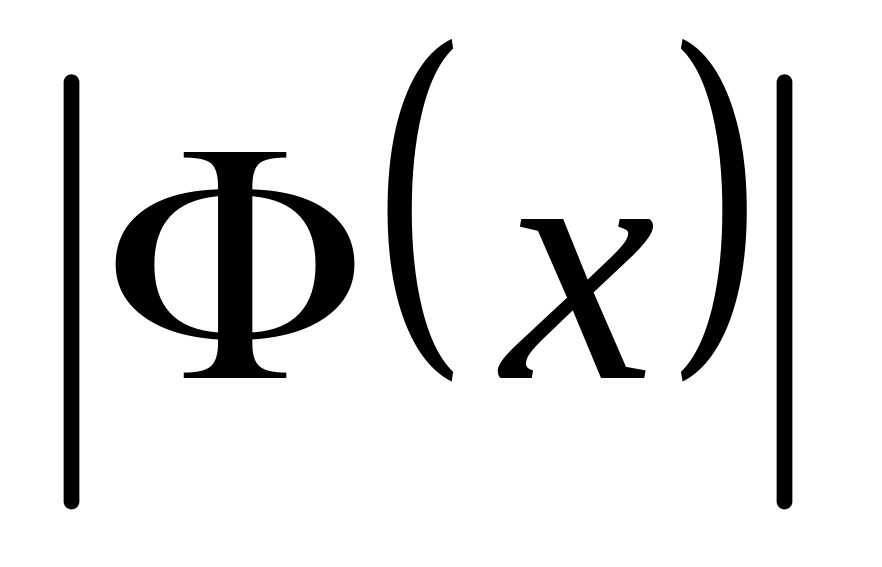 ограничена на
.
ограничена на
.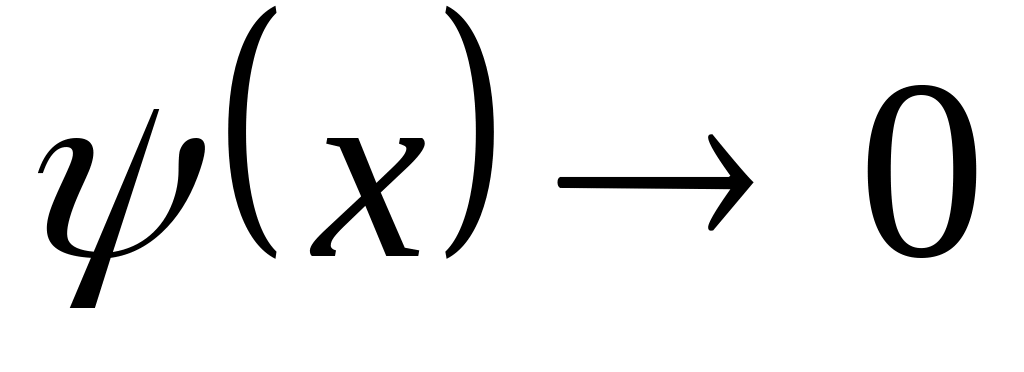 при
при
 .
.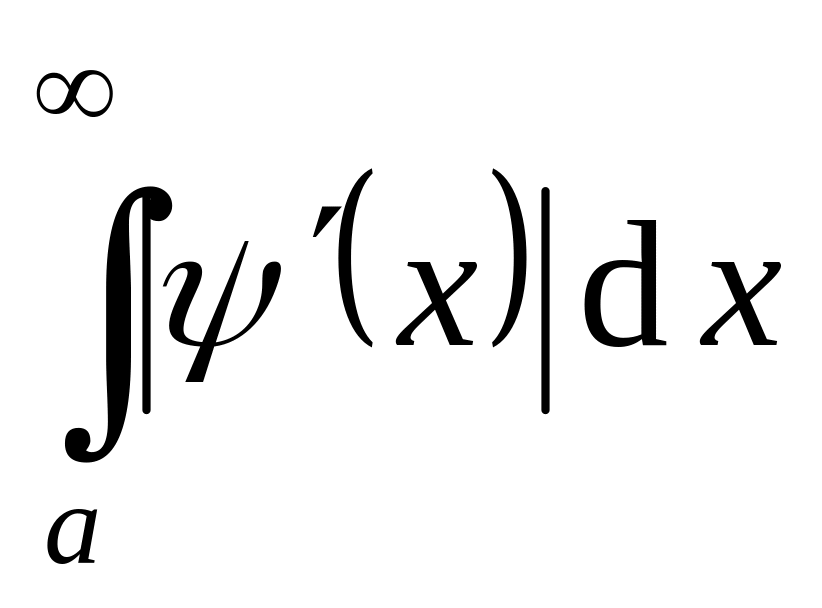 сходится.
сходится.
Действительно, т.к.
ограничена и
при
,
то
![]() ,
кроме того,
,
кроме того,
![]() ограничена, а т.к.
сходится, то сходится и
ограничена, а т.к.
сходится, то сходится и
![]() сходится
сходится
![]() .
.
Признак Дирихле: Пусть и непрерывны на , интегрируема на и пусть
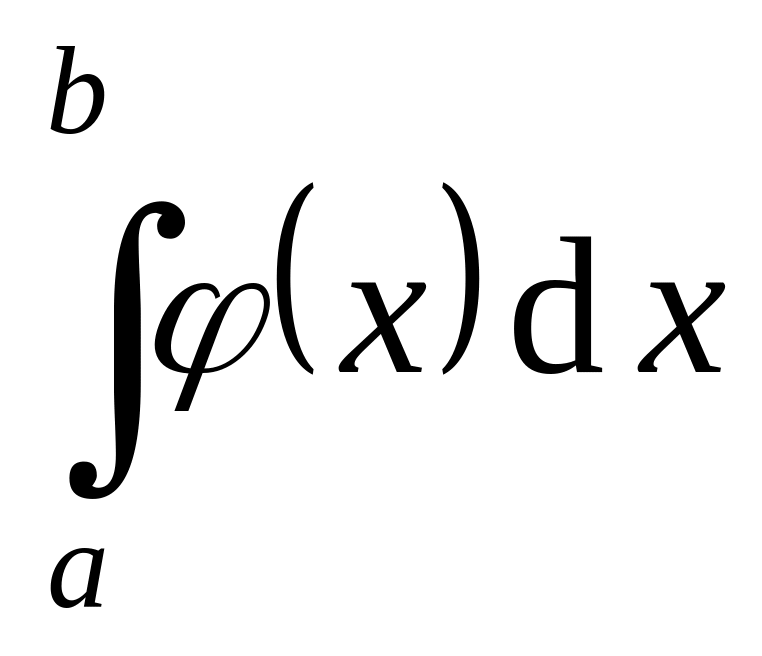 ограничен для
ограничен для
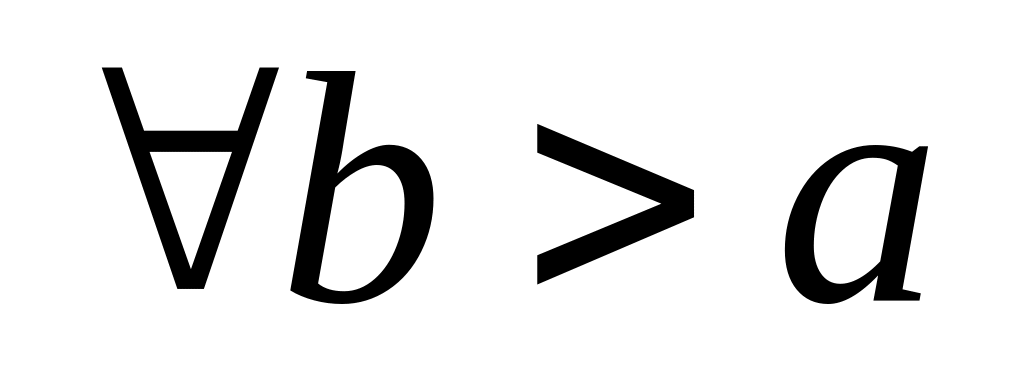 .
.монотонна на .
при .
Тогда сходится.
Проверим выполнение условий следствия специального признака.
Обозначая
 ,
видим, что
ограничена на
.
,
видим, что
ограничена на
.По условию при .
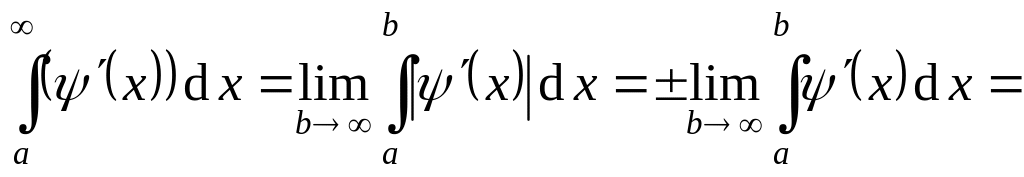 («+»,
если
(«+»,
если
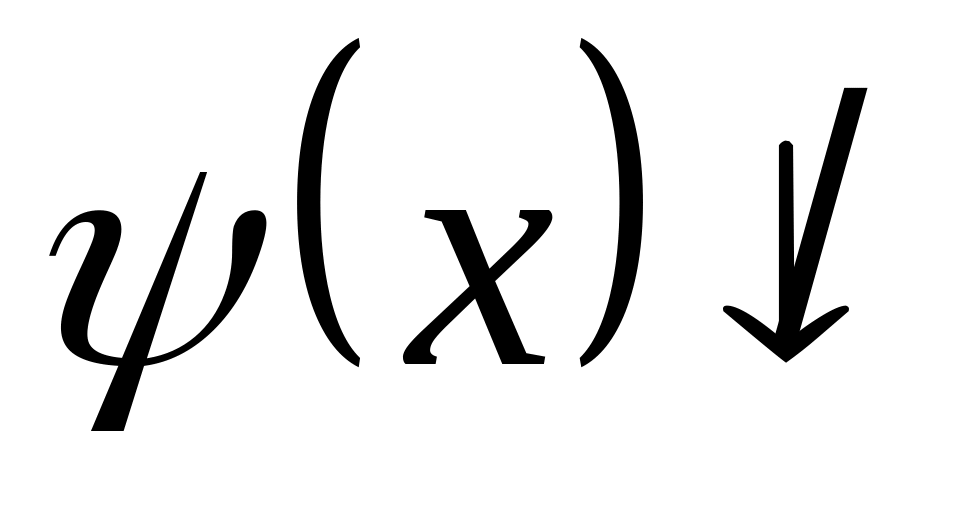 ,
«–», если
,
«–», если
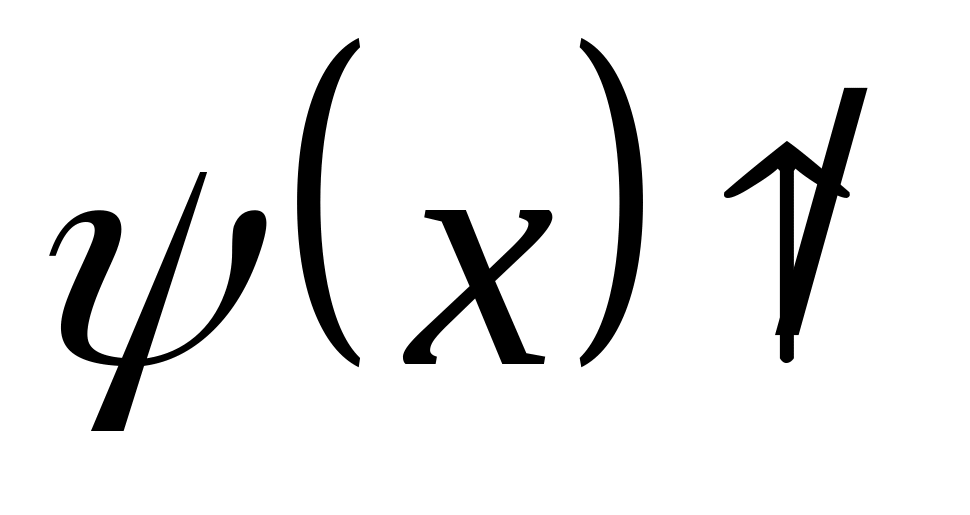 )
)
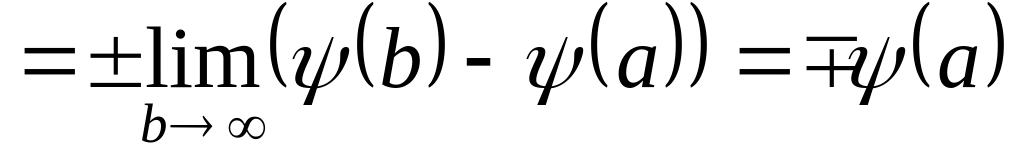 ,
т.е.
,
т.е.
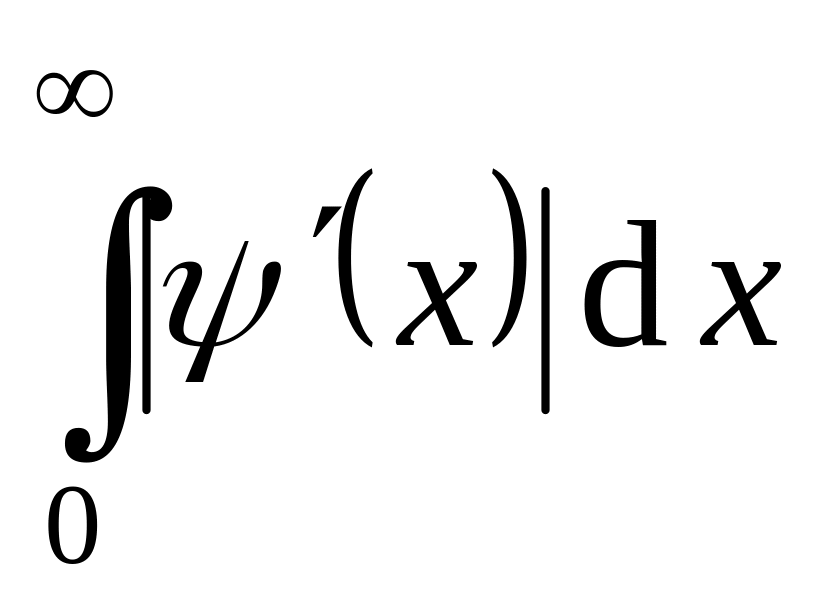 сходится.
сходится.
Следовательно, выполнены все условия специального признака и, значит, сходится.
Признак Абеля: Пусть
и
непрерывны на
,
интегрируема на
![]() и пусть
и пусть
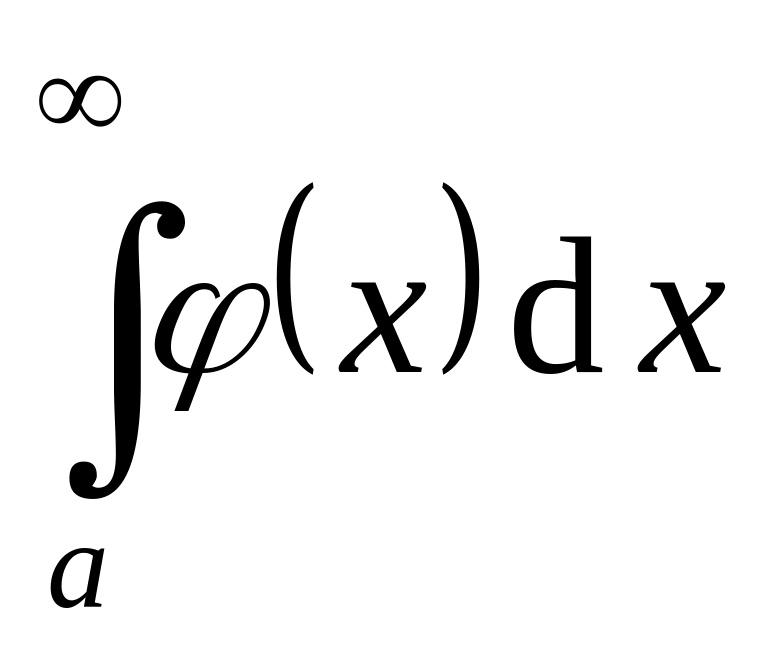 сходится.
сходится.монотонна и ограничена.
Тогда сходится.
Т.к.
монотонна и ограничена, то существует
конечный
![]() .
Тогда
.
Тогда
![]()
![]() .
Т.к.
сходится, то сходится
.
Т.к.
сходится, то сходится
![]() ,
а
,
а
![]() сходится по признаку Дирихле, т.к.
ограничен,
сходится по признаку Дирихле, т.к.
ограничен,
![]() монотонна и
монотонна и
![]() при
.
Следовательно,
сходится.
при
.
Следовательно,
сходится.
Признаки Дирихле и Абеля только достаточны. Расходимость с их помощью показать нельзя.
Числовые ряды
Простейшие свойства:
Ряды
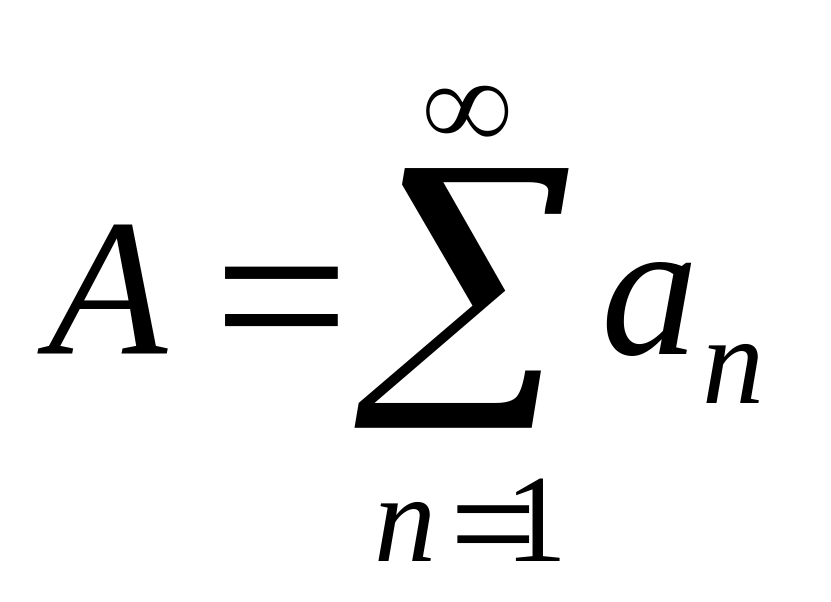 и
и
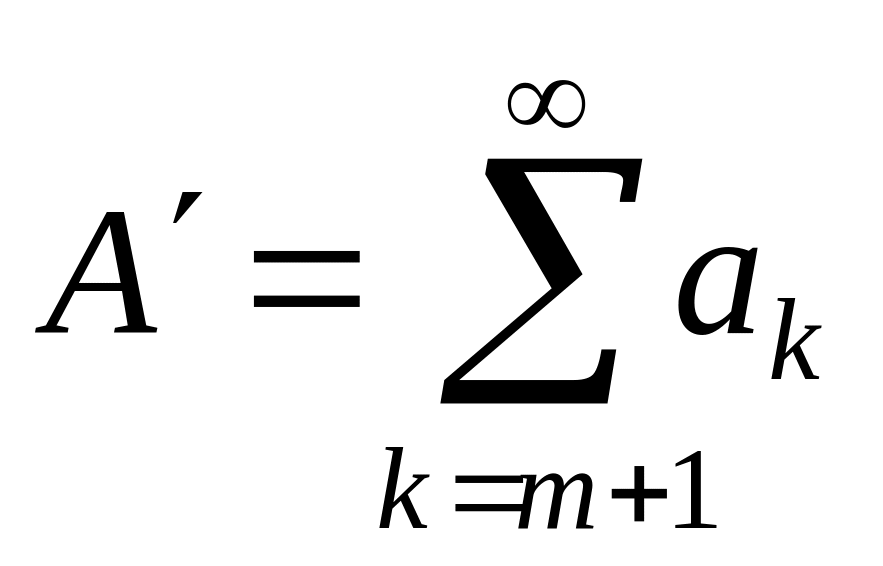 либо оба сходятся, либо оба расходятся.
(Очевидно, т.к. критерий Коши даёт
для обоих рядов одно и то же неравенство.
При этом если ряды сходятся, то
либо оба сходятся, либо оба расходятся.
(Очевидно, т.к. критерий Коши даёт
для обоих рядов одно и то же неравенство.
При этом если ряды сходятся, то
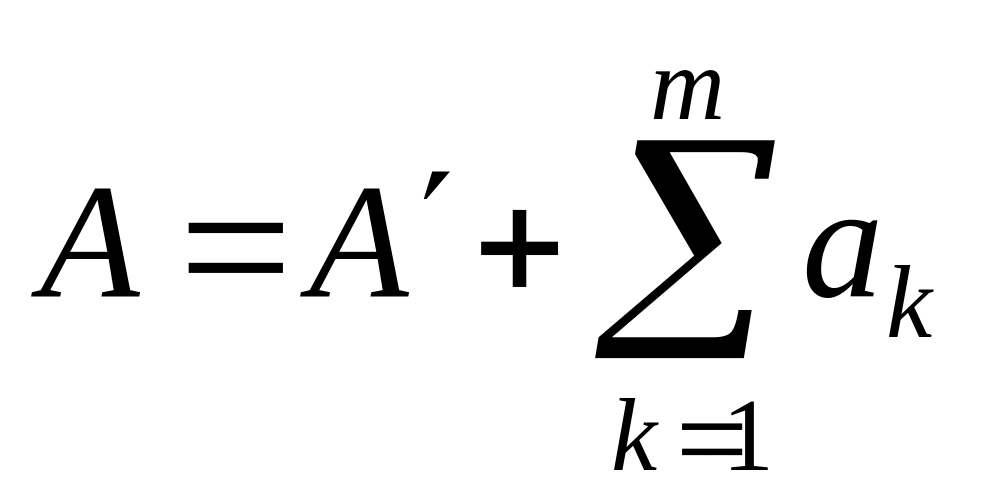 ).
).Пусть
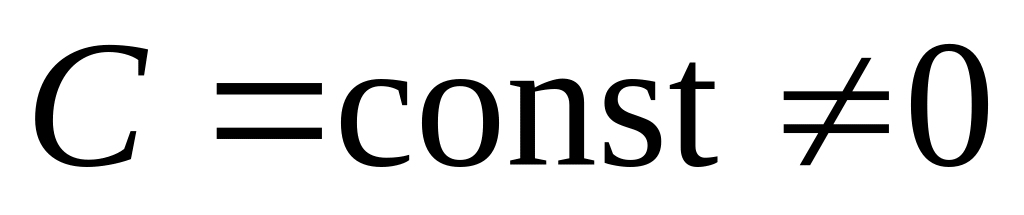 .
Тогда
.
Тогда
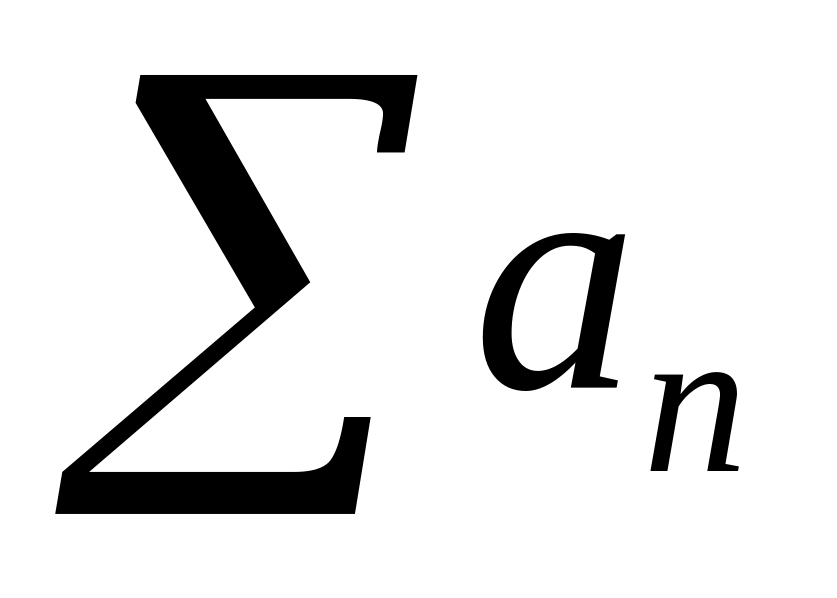 и
и
 либо оба сходятся, либо оба расходятся.
(Если обозначить
либо оба сходятся, либо оба расходятся.
(Если обозначить
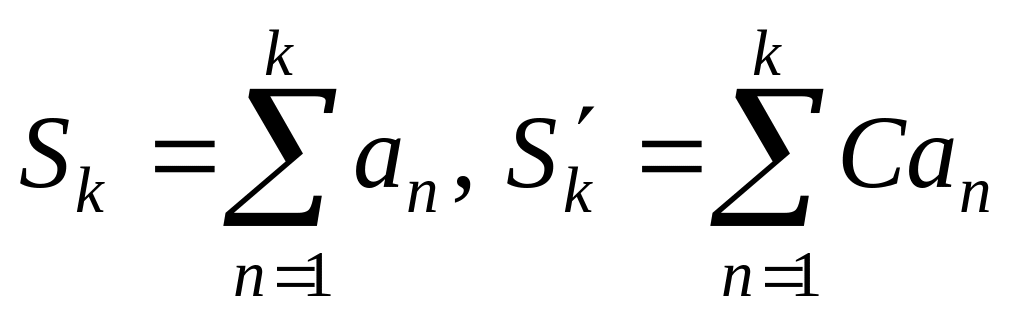 ,
то ясно, что
,
то ясно, что
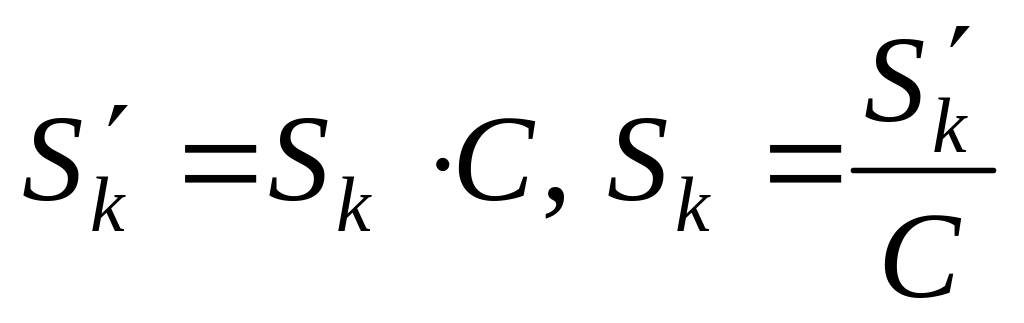 .
Отсюда, если
.
Отсюда, если
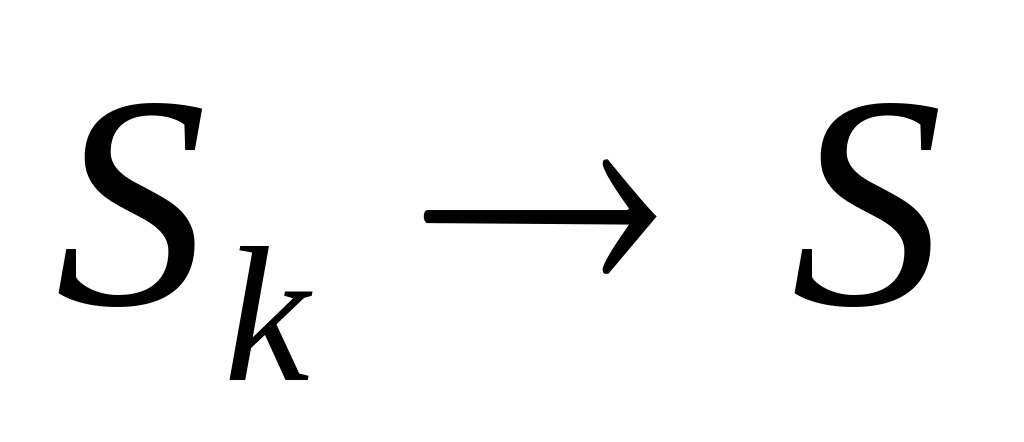 ,
то
,
то
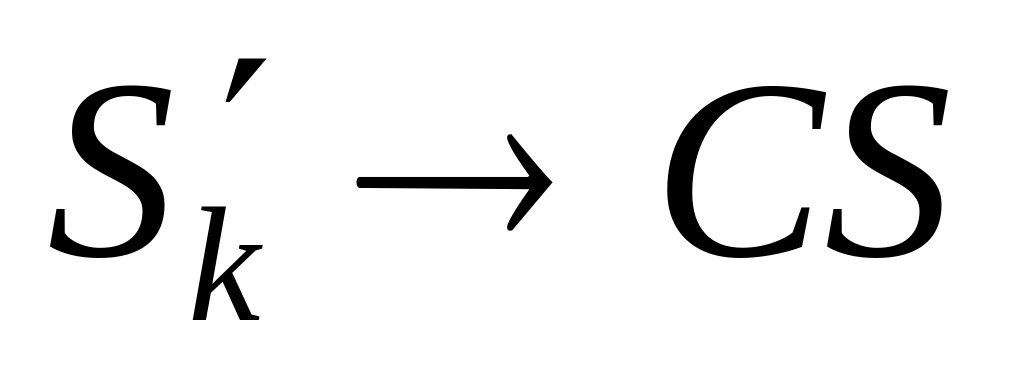 и т.п.).
и т.п.).Если и
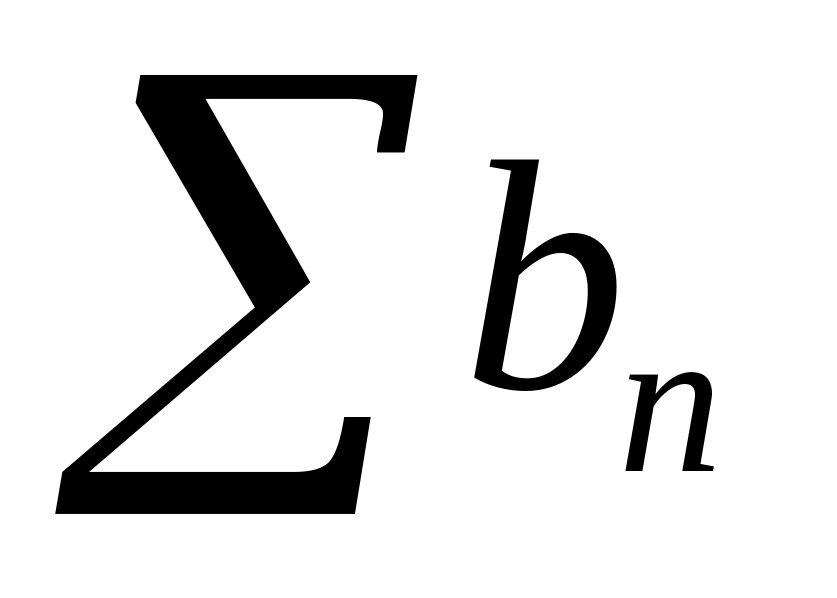 оба сходятся, то при
оба сходятся, то при
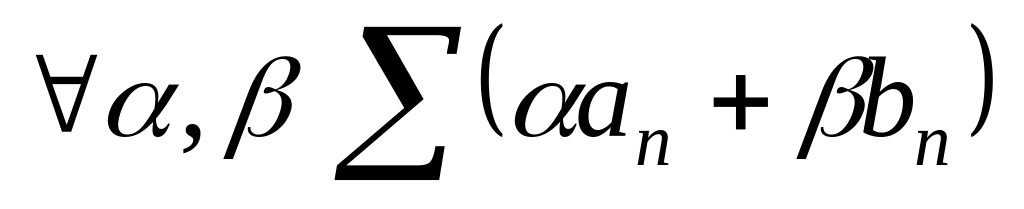 тоже сходится, причём
тоже сходится, причём
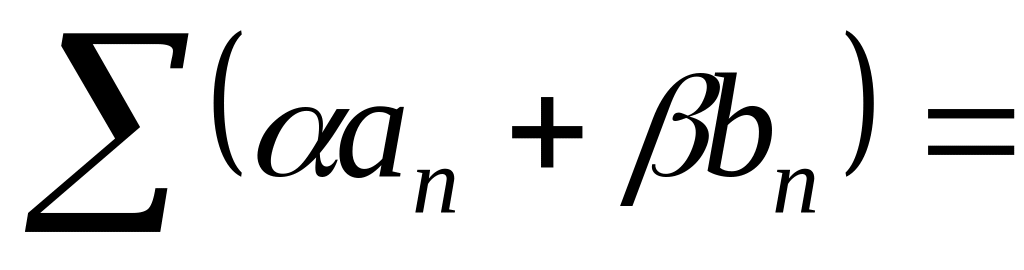
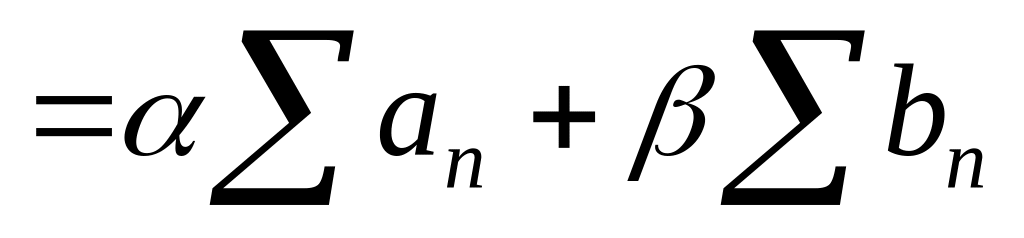 .
(
.
(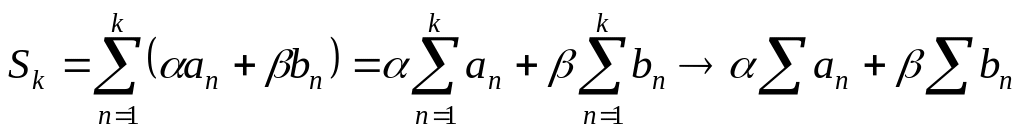 при
при
 ).
).
Ряды с положительными членами
Если
![]() ,
то
,
то
![]() не убывает. (Действительно,
не убывает. (Действительно,
![]() для
для
![]() ,
т.е.
,
т.е.
![]() ).
).
Необходимый и достаточный признак сходимости: Если , то сходится тогда и только тогда, когда ограничена (сверху).
То, что ряд сходится, равносильно тому,
что существует конечный
![]() ,
а это, т.к.
,
а это, т.к.
![]() не убывает, равносильно ограниченности
сверху
.
не убывает, равносильно ограниченности
сверху
.
I признак сравнения:
Если
![]() ,
то из сходимости
следует сходимость
,
из расходимости
следует расходимость
.
,
то из сходимости
следует сходимость
,
из расходимости
следует расходимость
.
Пусть сходится. Обозначим
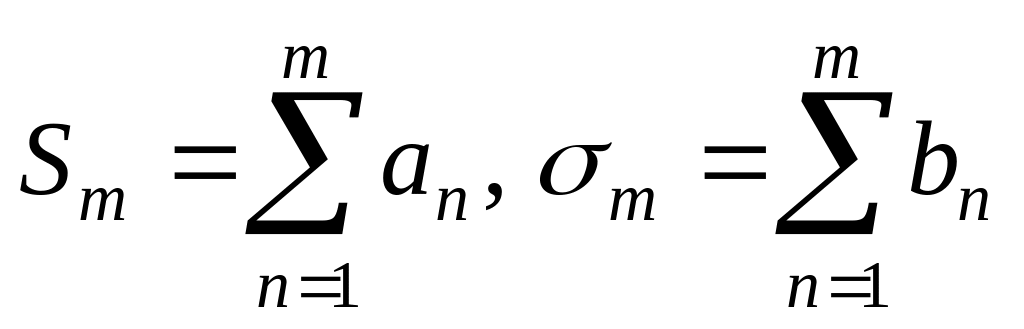 .
По необходимому и достаточному признаку
.
По необходимому и достаточному признаку
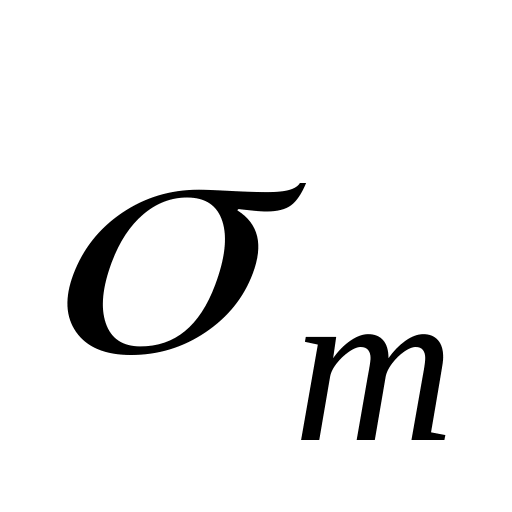 ограничена и
ограничена и
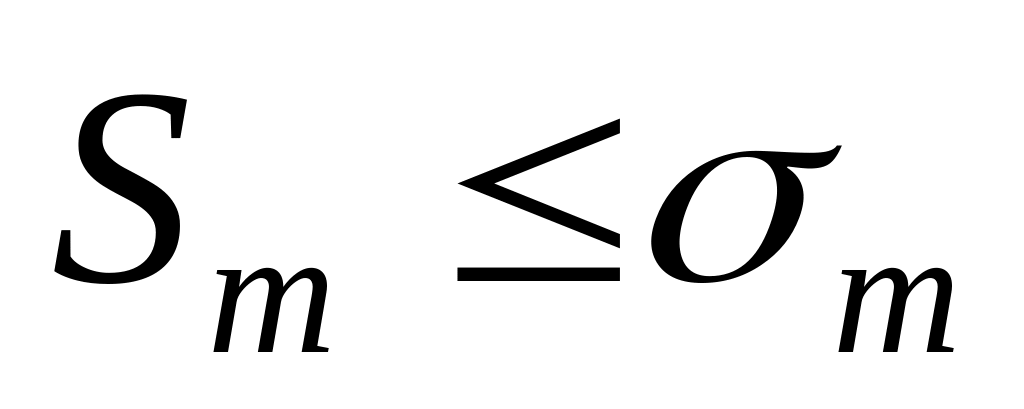 ,
т.е.
тоже ограничена, а значит сходится.
,
т.е.
тоже ограничена, а значит сходится.Пусть расходится. Тогда
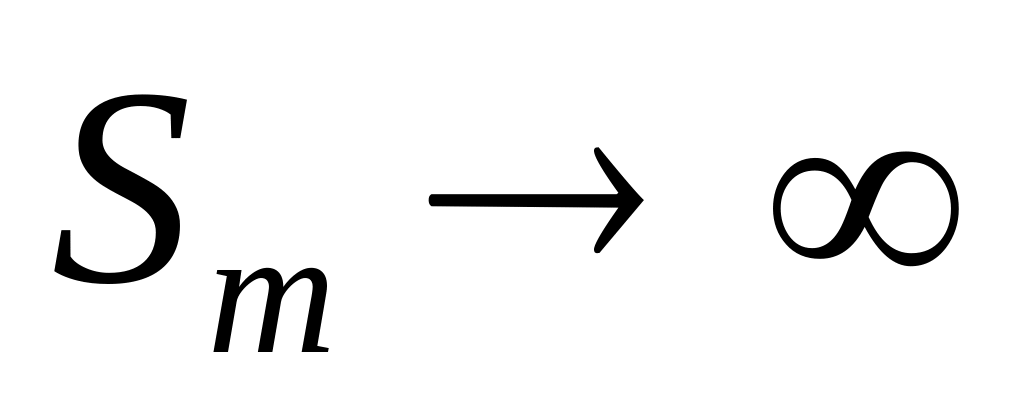 при
при
 .
Но
.
Но
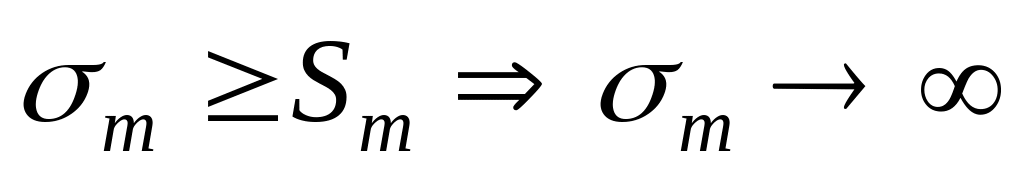 ,
т.е.
расходится.
,
т.е.
расходится.
II признак сходимости:
Если
![]() и существует конечный
и существует конечный
![]() ,
то
и
либо оба сходятся, либо оба расходятся
(в частности, если
,
то
и
либо оба сходятся, либо оба расходятся
(в частности, если
![]() (т.е.
(т.е.
![]() )).
)).
Возьмём
![]() .
Тогда
.
Тогда
![]() для
для
![]() будет
будет
![]() ,
т.е.
,
т.е.
![]() для
.
Отсюда:
для
.
Отсюда:
Если
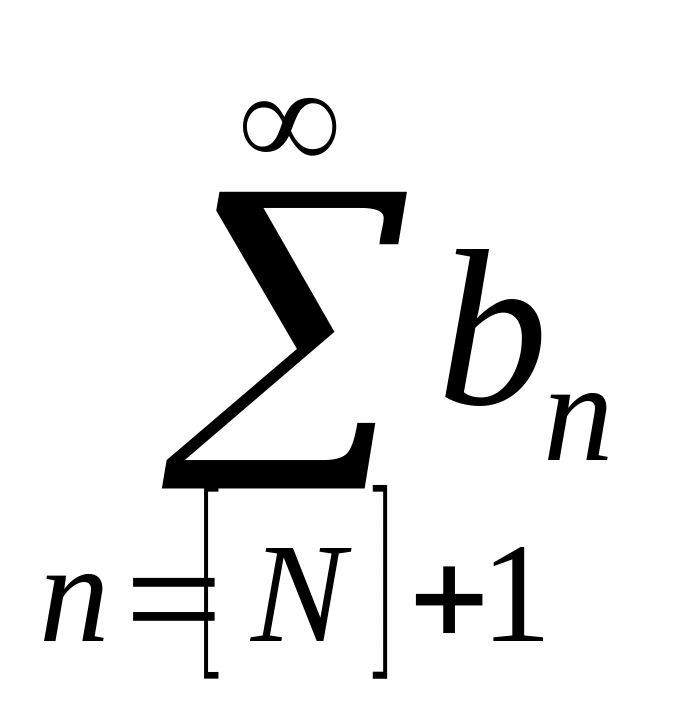 сходится, то
сходится, то
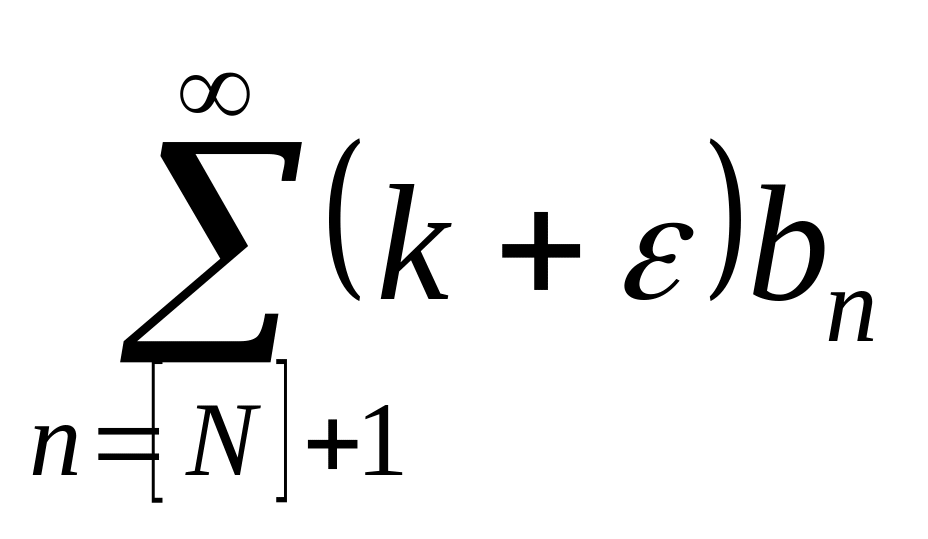 сходится и
сходится и
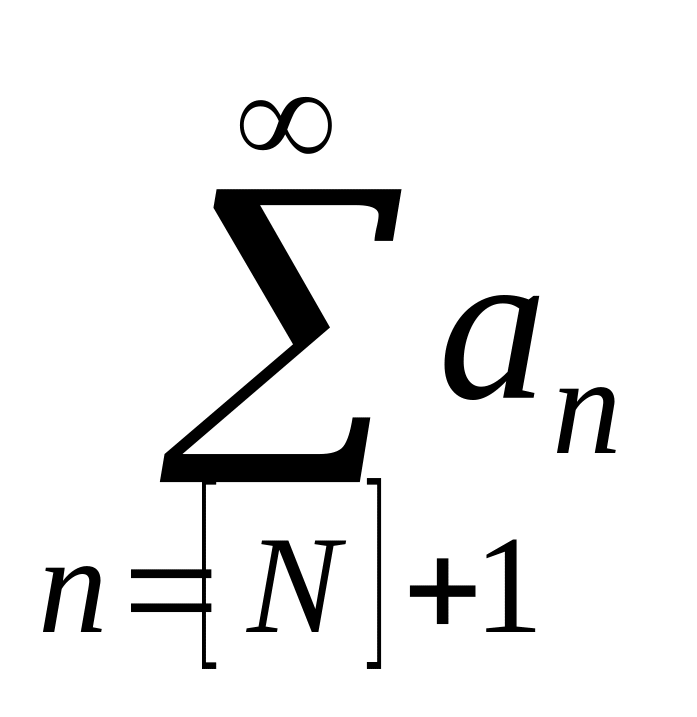 тоже сходится, следовательно,
сходится.
тоже сходится, следовательно,
сходится.Если сходится, то сходится и и
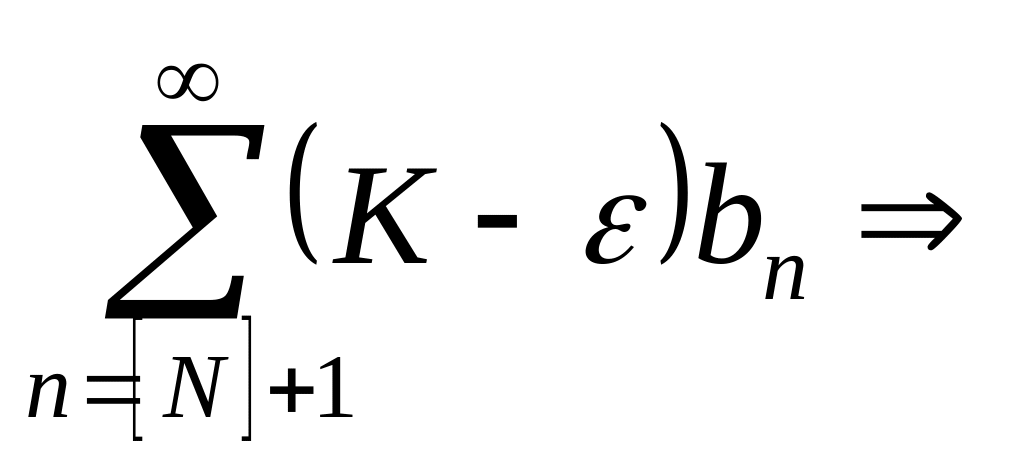 сходится
сходится
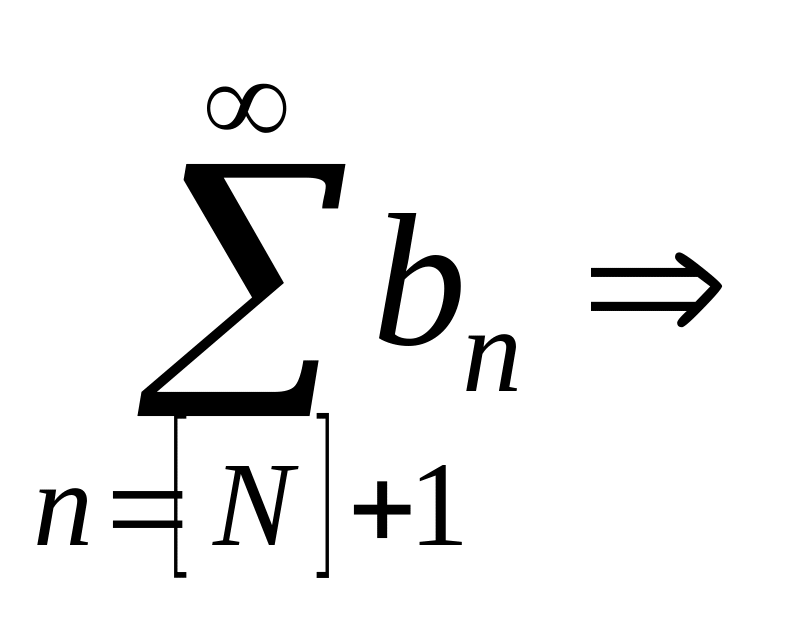 сходится
.
сходится
.
III признак сходимости:
Пусть
и
![]() .
Тогда из сходимости
следует сходимость
,
из расходимости
следует расходимость
.
.
Тогда из сходимости
следует сходимость
,
из расходимости
следует расходимость
.
Имеем
![]() для
для
![]() .
Перемножим эти неравенства. Тогда
.
Перемножим эти неравенства. Тогда
![]() ,
т.е.
,
т.е.
![]() .
Отсюда по первому признаку если
сходится, то и
сходится, если
расходится, то и
расходится.
.
Отсюда по первому признаку если
сходится, то и
сходится, если
расходится, то и
расходится.
Радикальный признак Коши: Пусть
![]() .
.
Если для , начиная с некоторого,
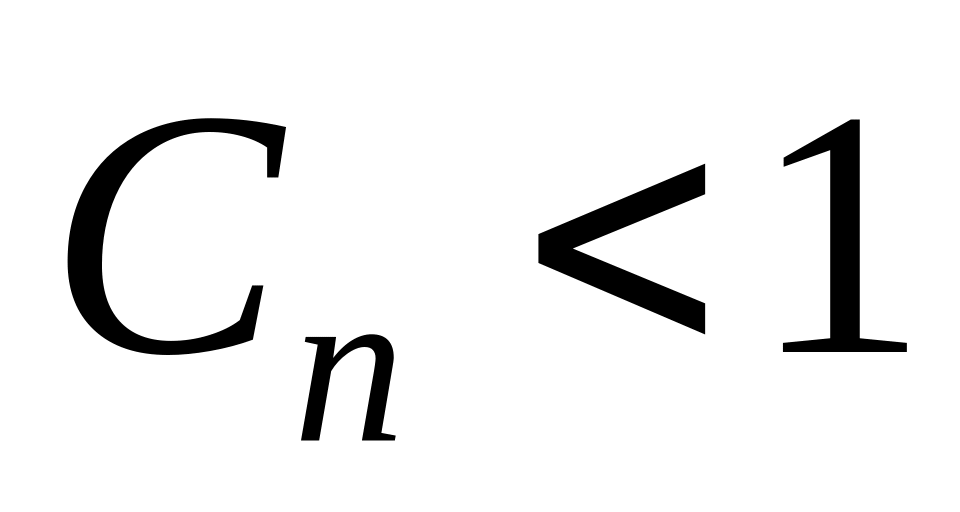 ,
то
сходится. Если же для
,
начиная с некоторого
,
то
сходится. Если же для
,
начиная с некоторого
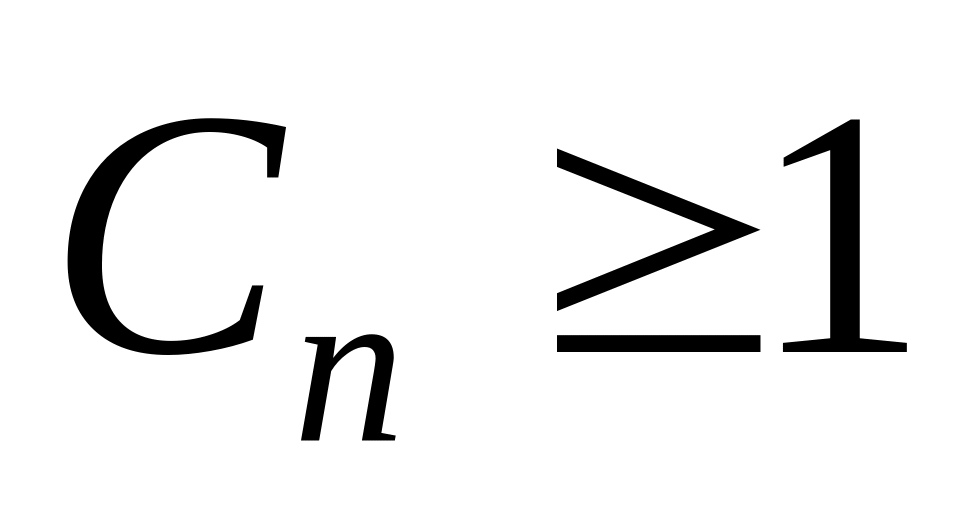 ,
то
расходится.
,
то
расходится.Если
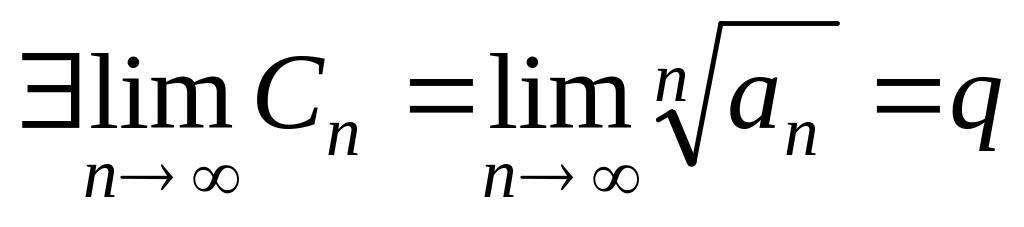 ,
то при
,
то при
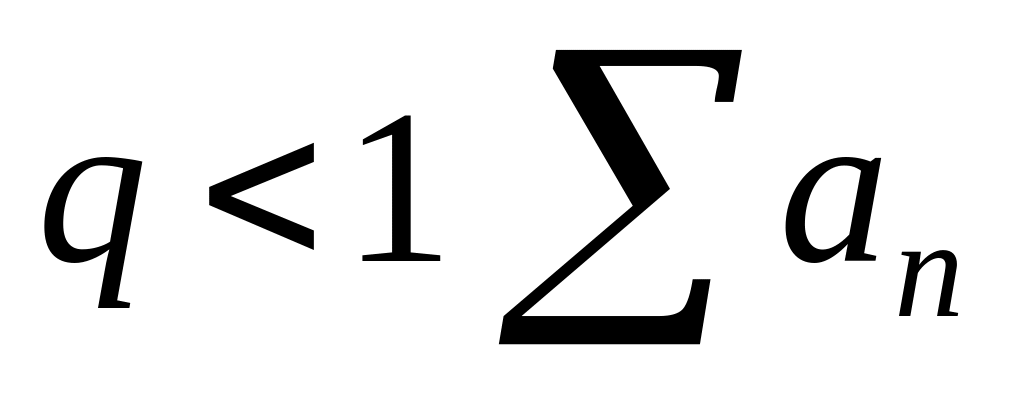 сходится, при
сходится, при
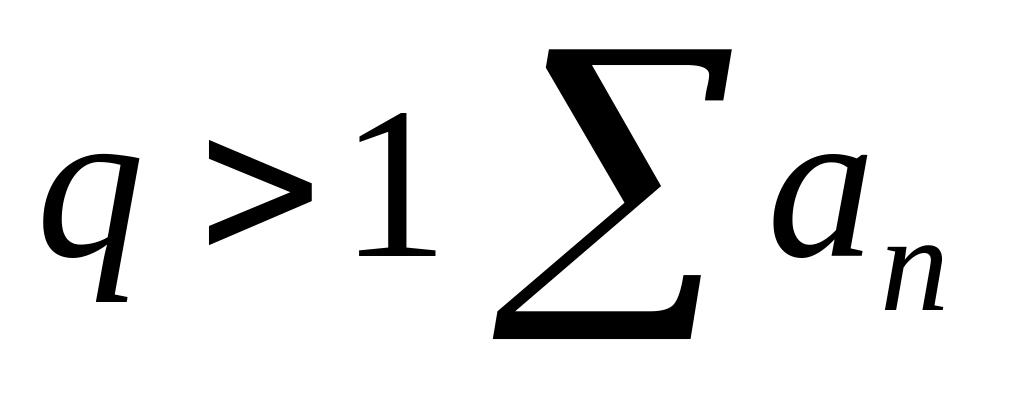 расходится.
расходится.
Сравним с рядом
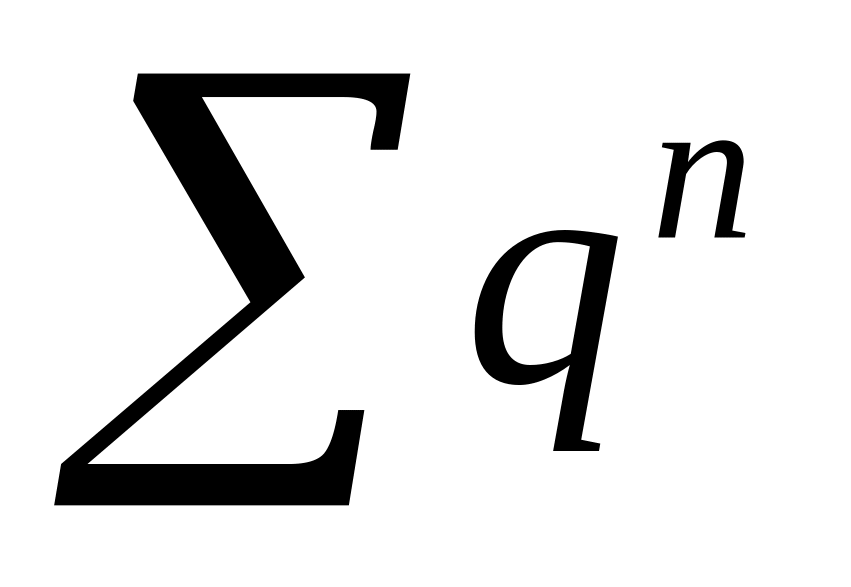 для случая
для случая
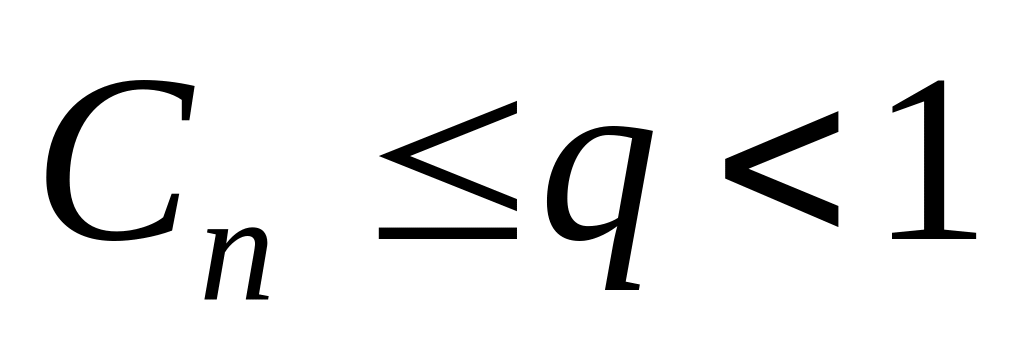 и с
и с
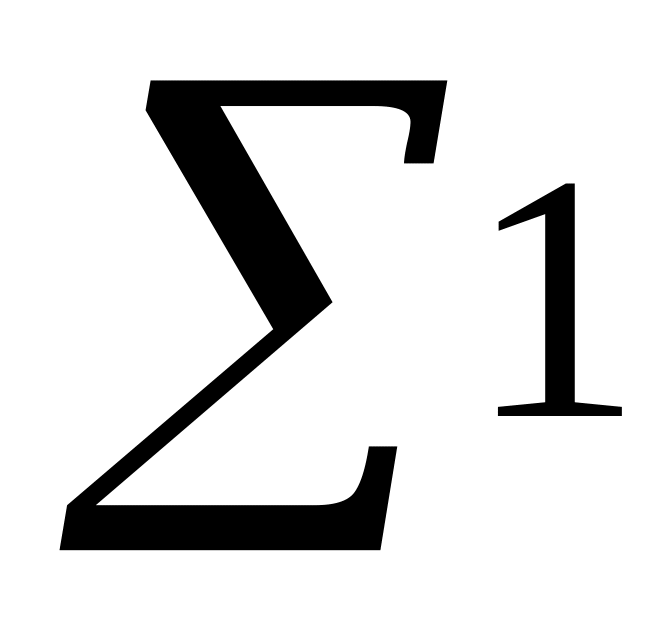 для
.
Тогда в первом случае, т.к.
для
.
Тогда в первом случае, т.к.
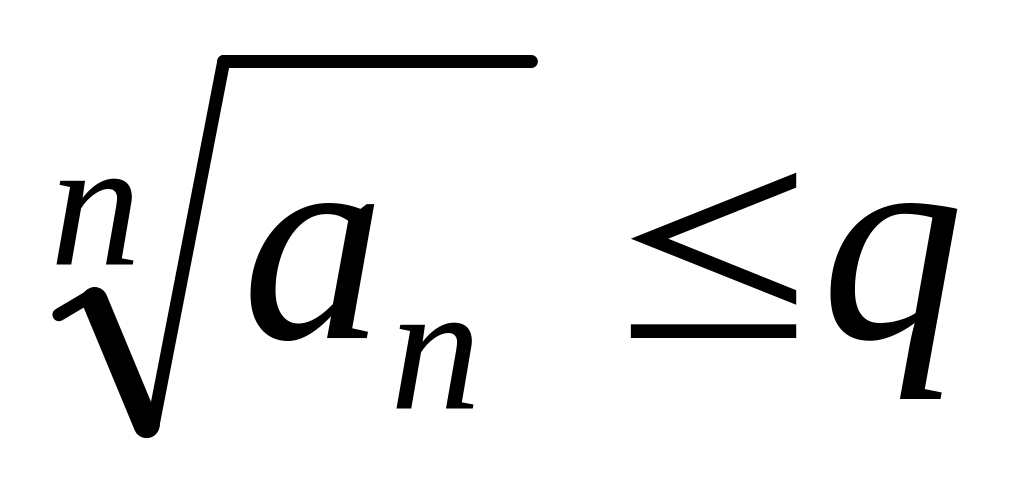 ,
то
,
то
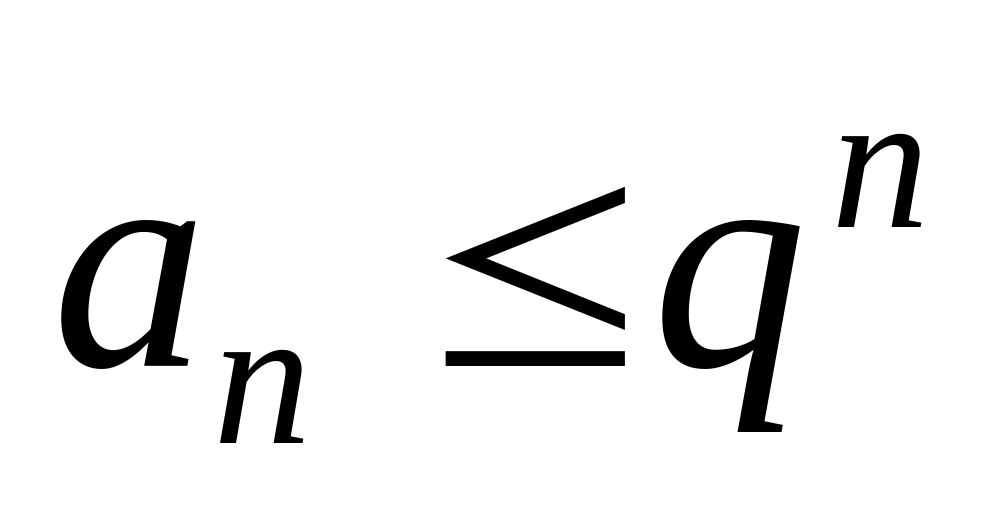 и т.к.
и т.к.
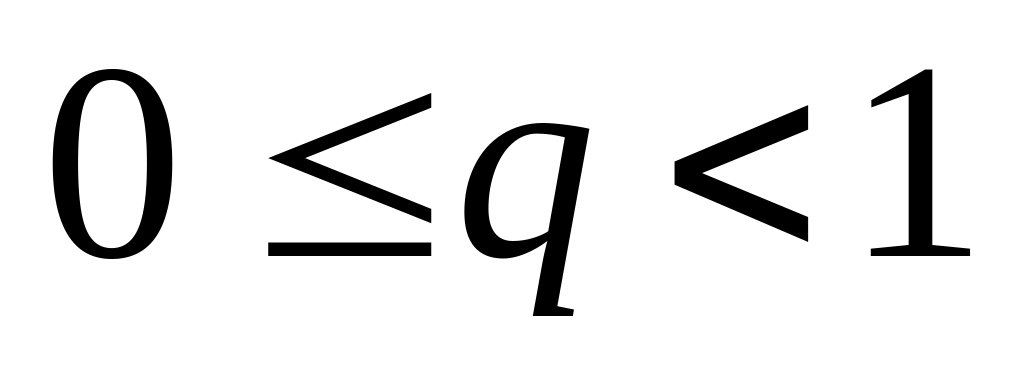 ,
то
сходится
,
то
сходится
 сходится. Во втором случае
сходится. Во втором случае
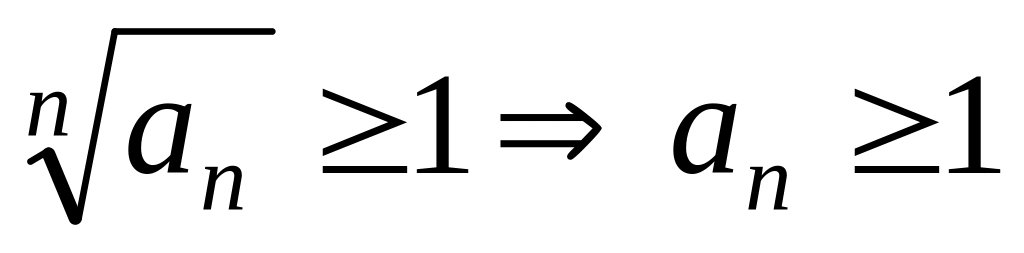 ,
начиная с некоторого n.
расходится
расходится.
,
начиная с некоторого n.
расходится
расходится.Пусть теперь
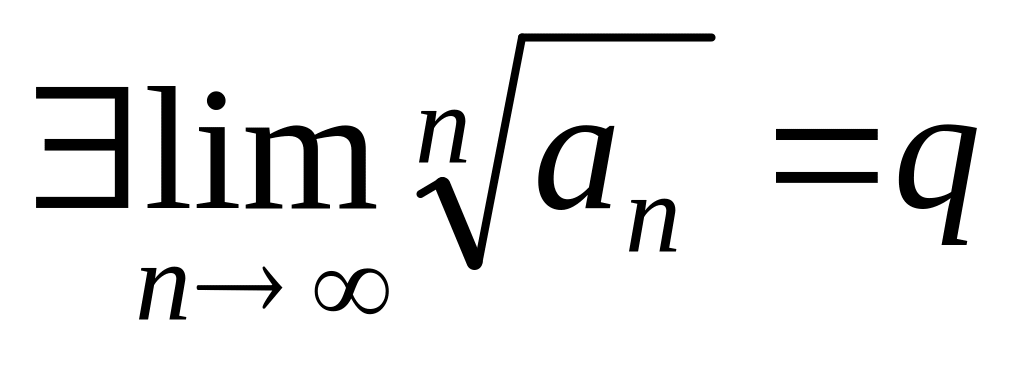 .
Если
.
Если
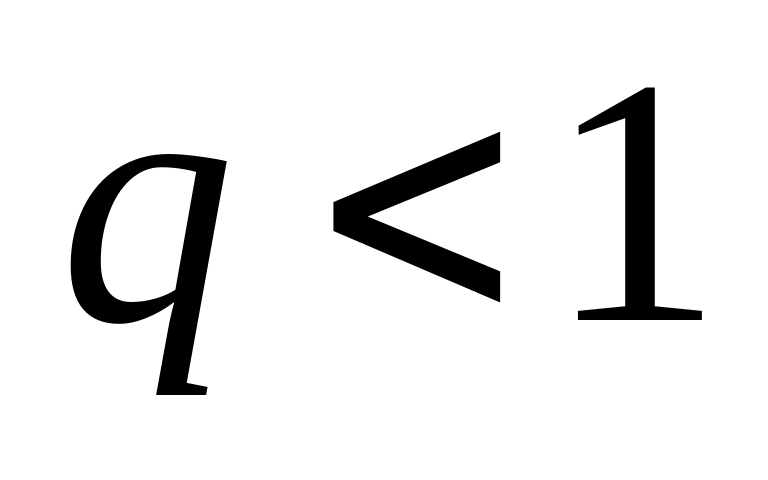 ,
то найдётся
,
то найдётся
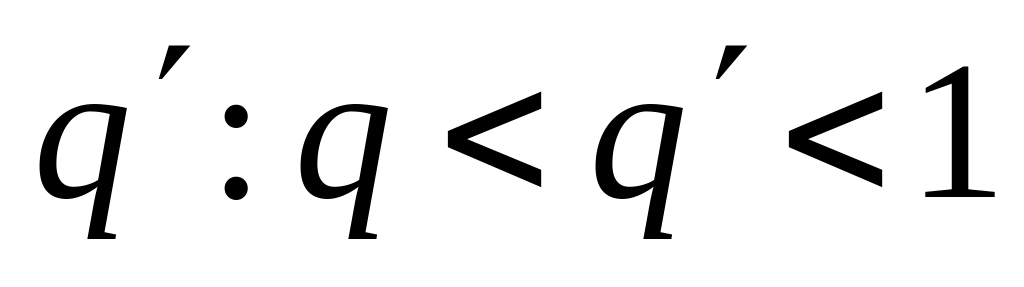 и для
,
начиная с некоторого, будет
и для
,
начиная с некоторого, будет
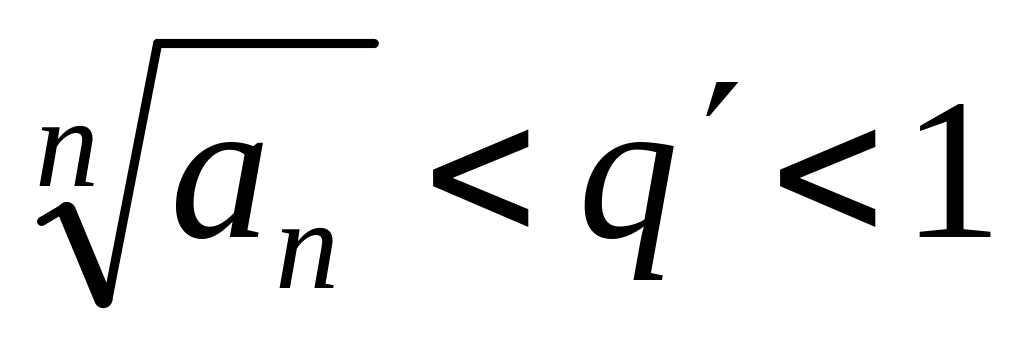 .
Отсюда
сходится.
.
Отсюда
сходится.
Признак Даламбера: Пусть
![]() .
.
Если при , начиная с некоторого, будет
 ,
то
сходится, если же
,
то
сходится, если же
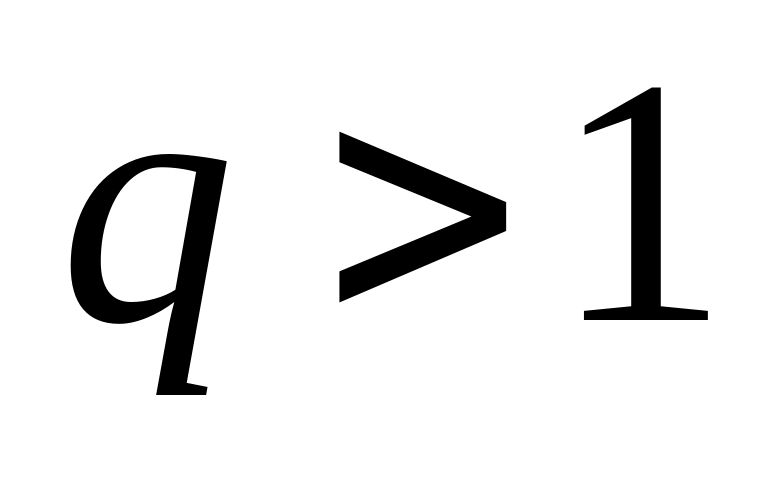 ,
то
расходится.
,
то
расходится.
Если
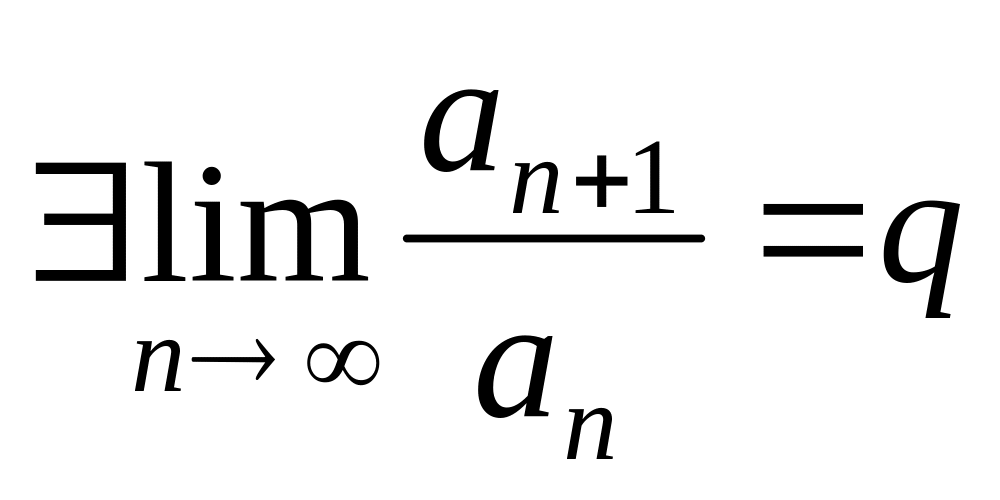 ,
то при
ряд сходится, при
– расходится.
,
то при
ряд сходится, при
– расходится.
Применим к и рядам
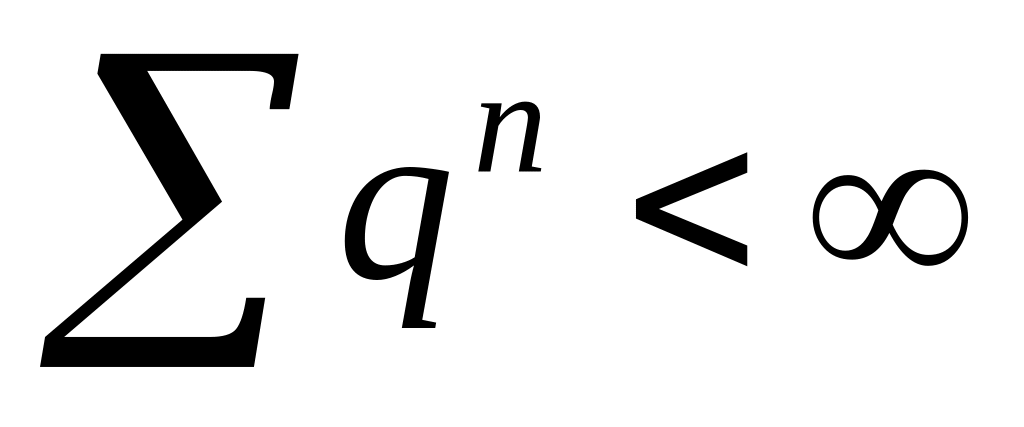 (при
)
и
III признак сходимости.
Тогда в первом случае
(при
)
и
III признак сходимости.
Тогда в первом случае
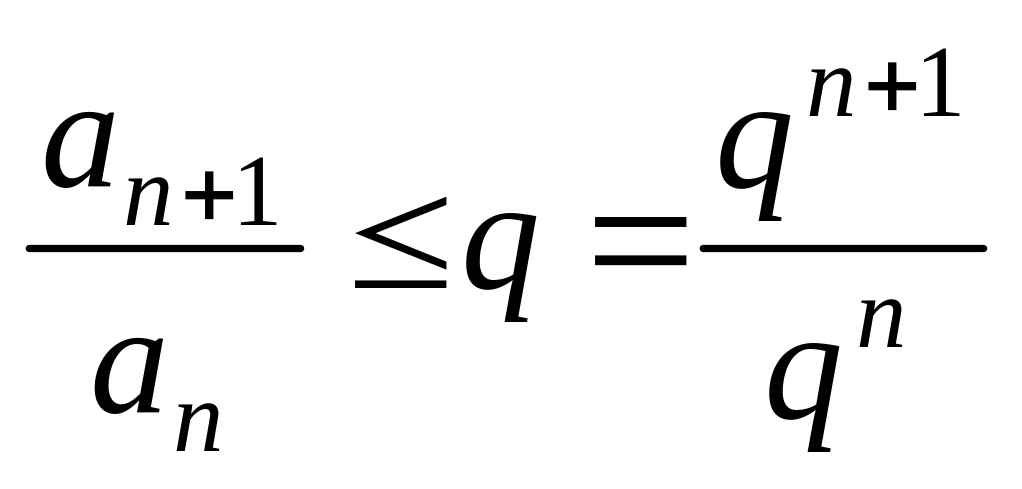 и
сходится. Следовательно,
сходится. Во втором случае
и
сходится. Следовательно,
сходится. Во втором случае
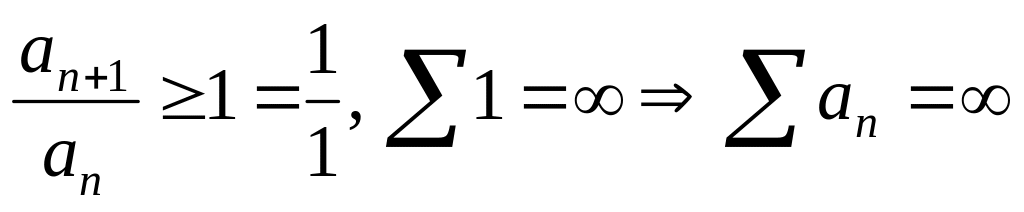 .
.Пусть . Тогда, если , то
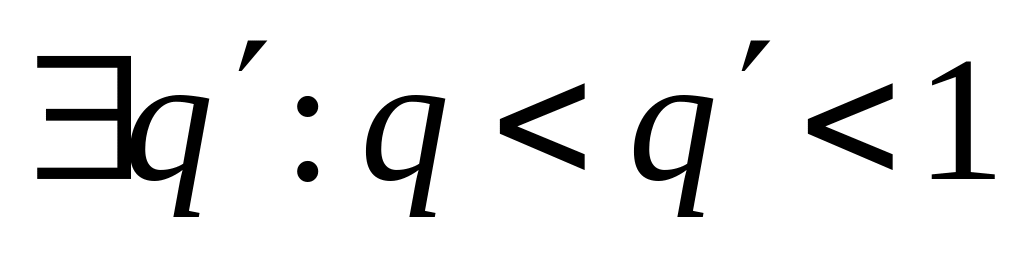 и
для
будет
и
для
будет
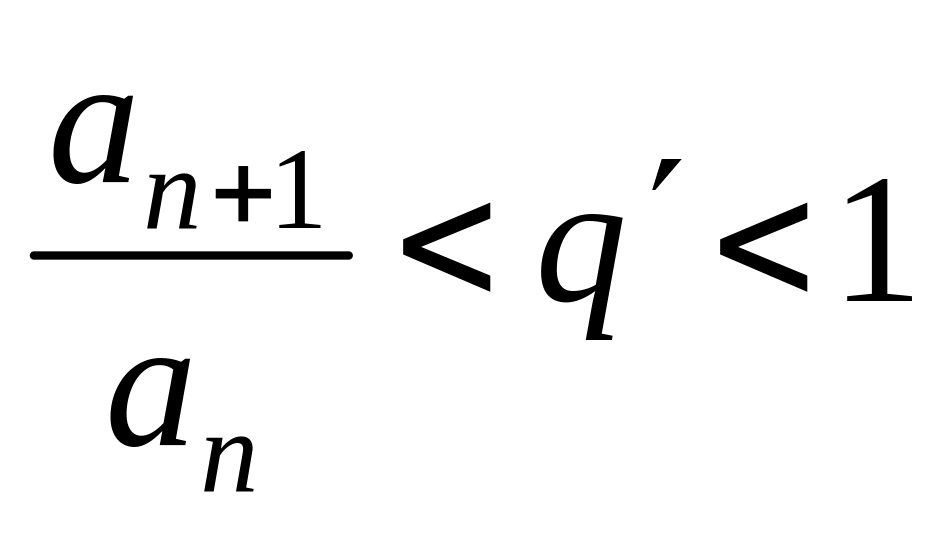 .
Следовательно, по первому случаю
сходится. Если же
,
то
для
будет
.
Следовательно, по первому случаю
сходится. Если же
,
то
для
будет
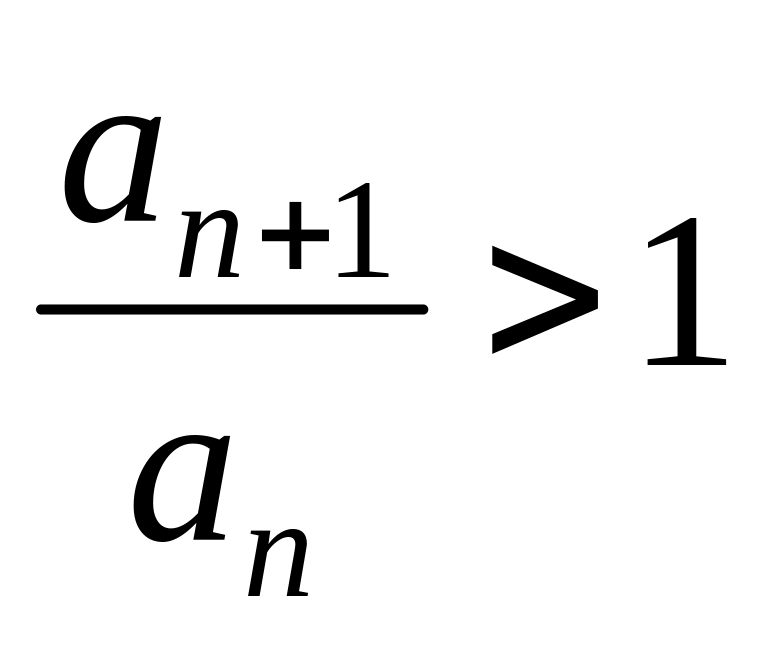 и
расходится.
и
расходится.
При
![]() как в признаке Даламбера, так и в признаке
Коши требуется дополнительное
исследование.
как в признаке Даламбера, так и в признаке
Коши требуется дополнительное
исследование.
Интегральный признак Коши-Маклорена:
Пусть
![]() ,
причём
непрерывна на
,
причём
непрерывна на
![]() ,
монотонно убывает и
.
Тогда
и
,
монотонно убывает и
.
Тогда
и
![]() либо оба сходятся, либо оба расходятся.
либо оба сходятся, либо оба расходятся.
Обозначим
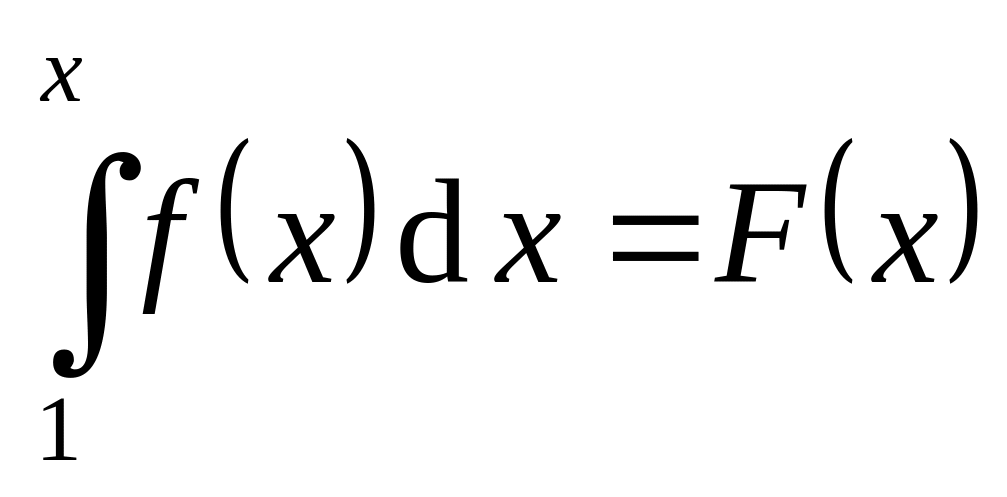 и заметим, что сходимость
эквивалентна существованию конечного
и заметим, что сходимость
эквивалентна существованию конечного
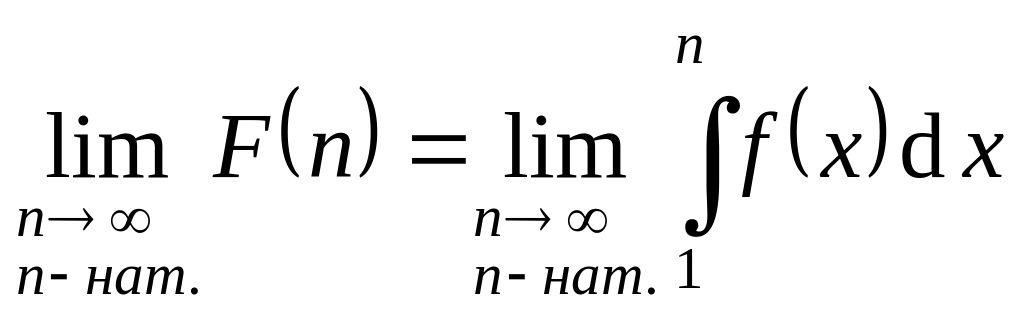 .
Действительно, т.к.
,
то для
.
Действительно, т.к.
,
то для
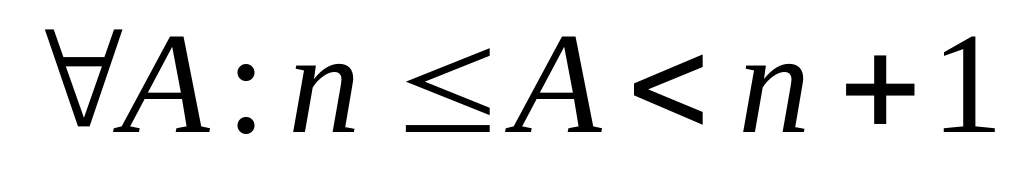 будет
будет
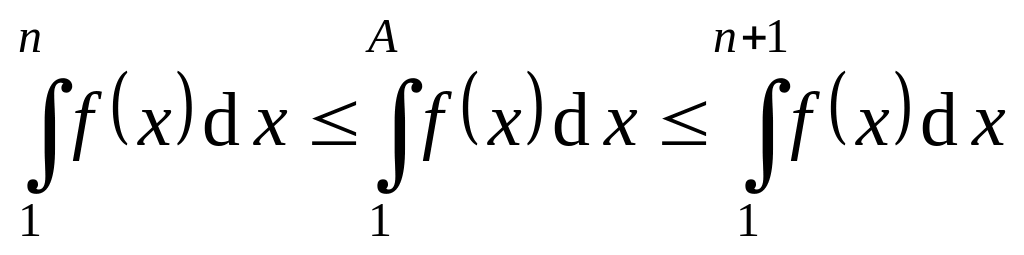 .
Поэтому, если
.
Поэтому, если
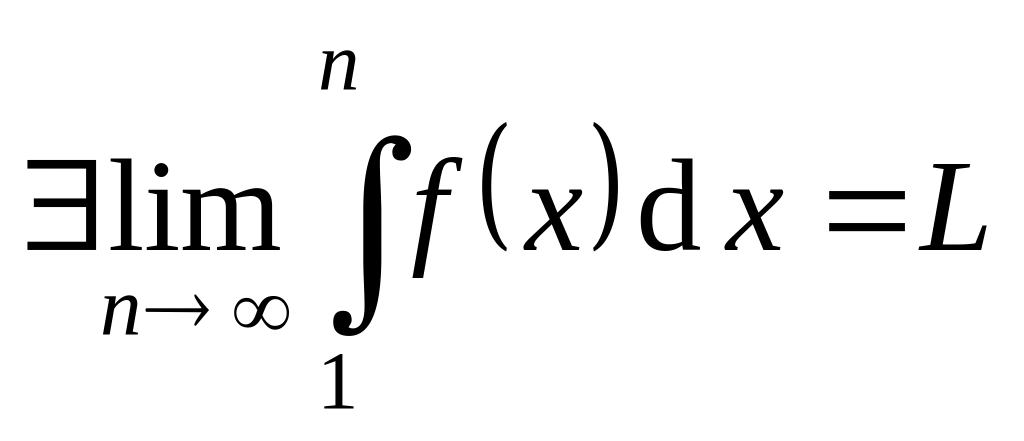 ,
то при
,
то при
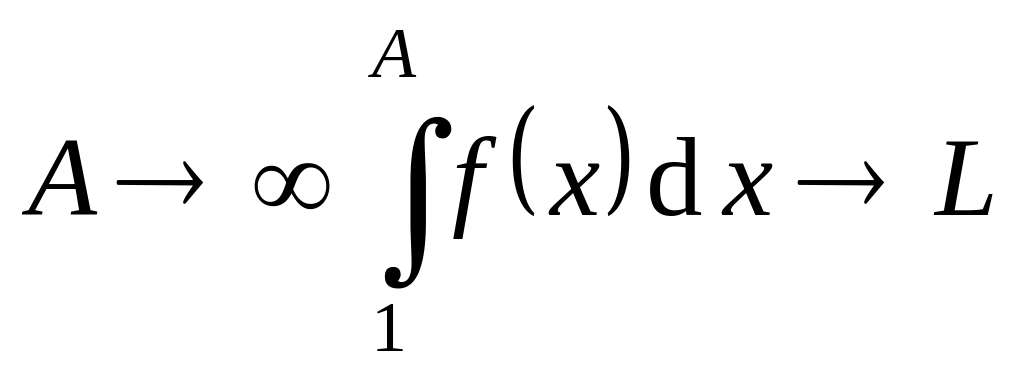 .
Если же
.
Если же
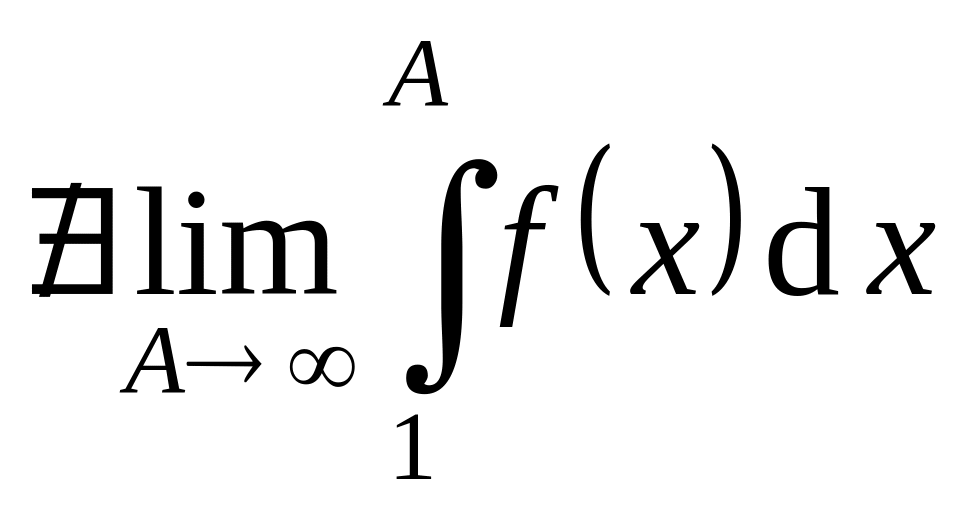 ,
то тем более
,
то тем более
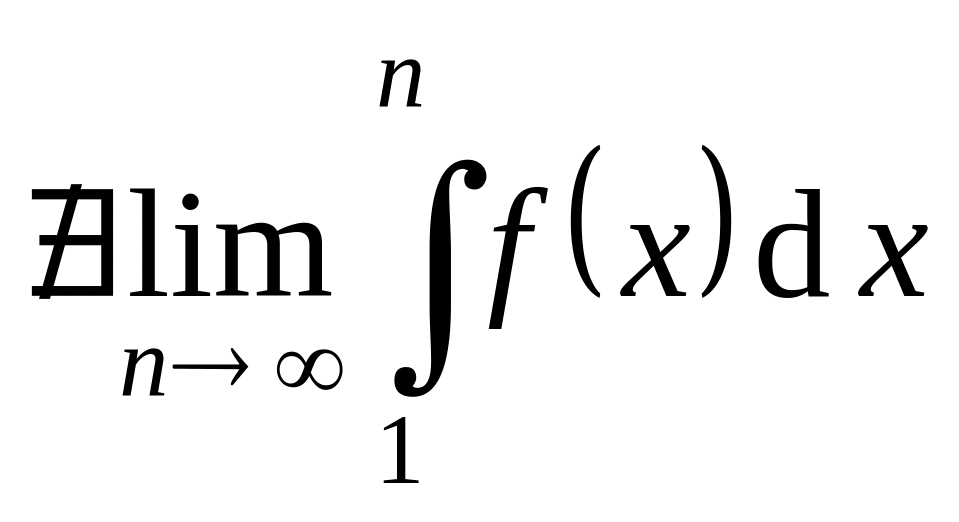 .
.Теперь заметим, что сходимость
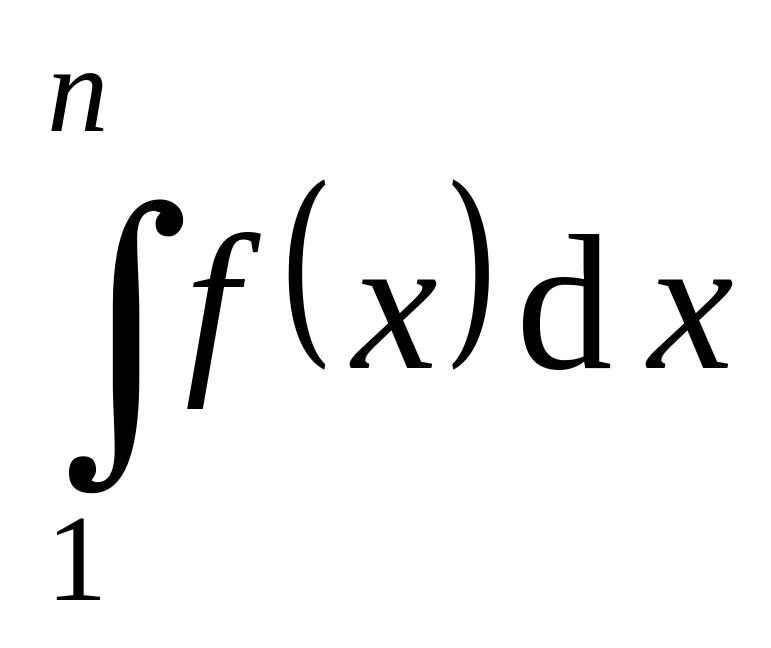 эквивалентна сходимости ряда
эквивалентна сходимости ряда
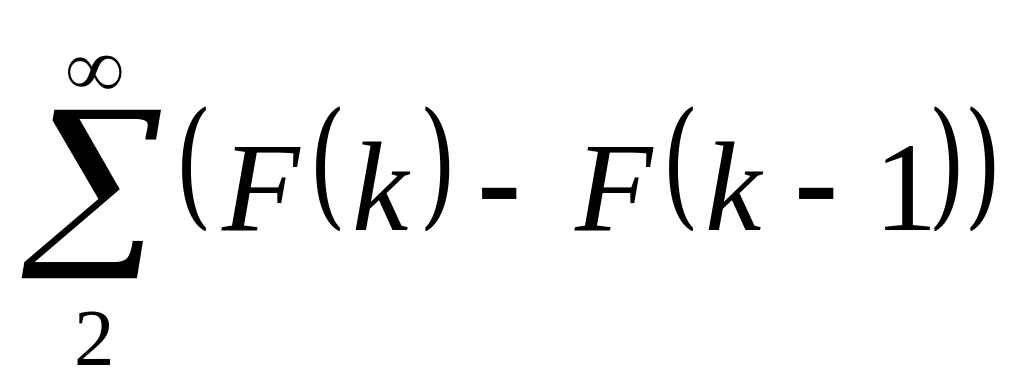 .
Действительно,
.
Действительно,
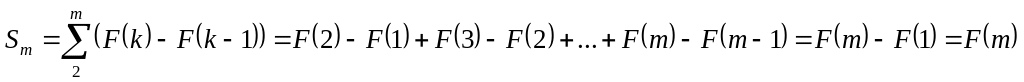 (т.к.
(т.к.
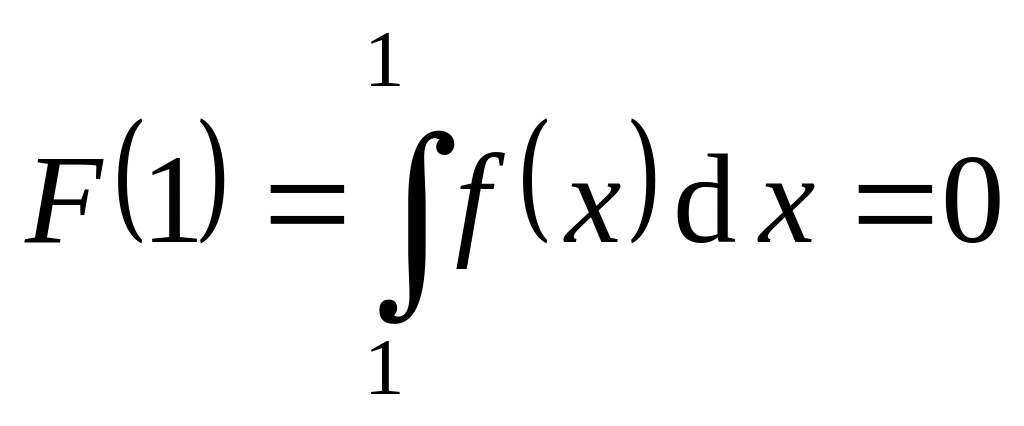 )
и сходимость
есть то же самое, что и сходимость
)
и сходимость
есть то же самое, что и сходимость
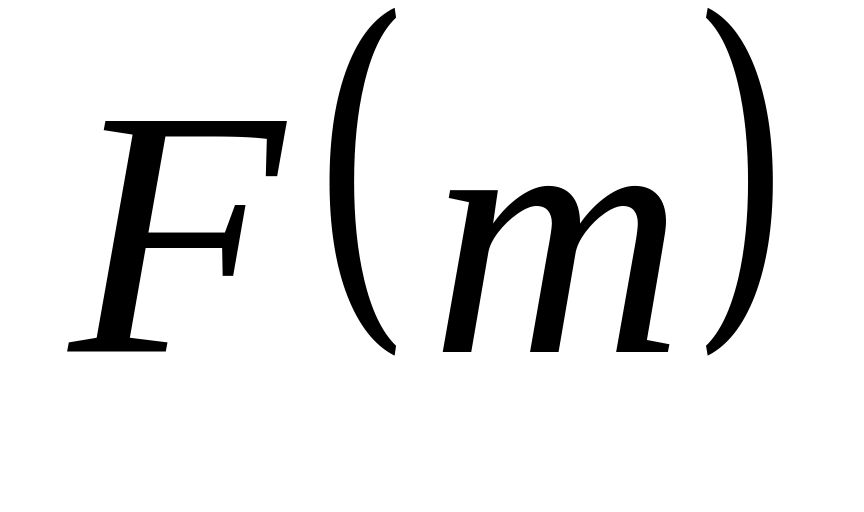 .
.Сравним с
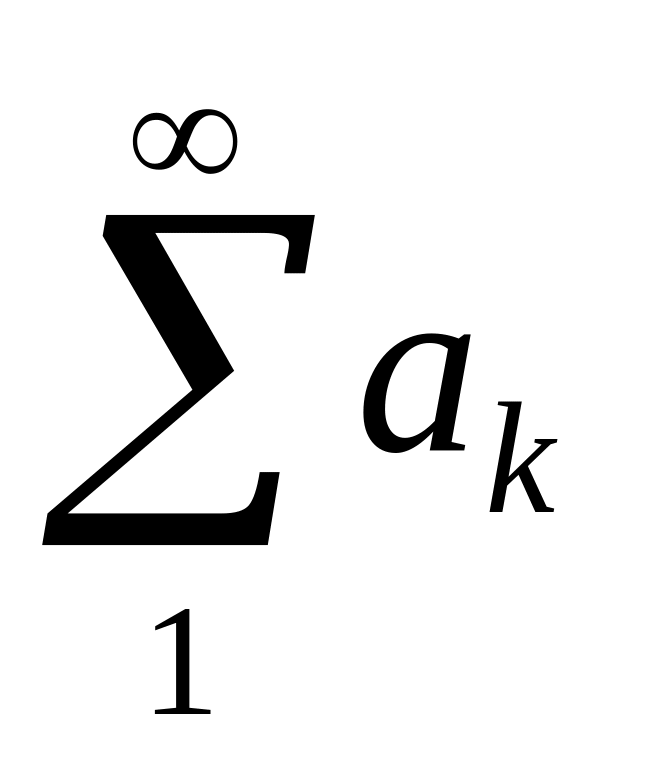 .
Имеем
.
Имеем
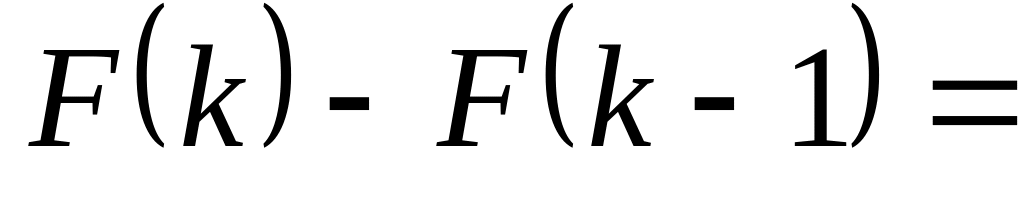 (по
теореме Лагранжа)
(по
теореме Лагранжа)
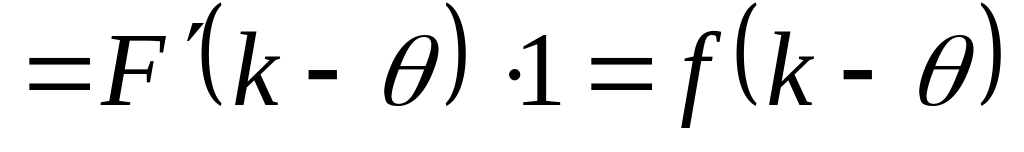 ,
где
,
где
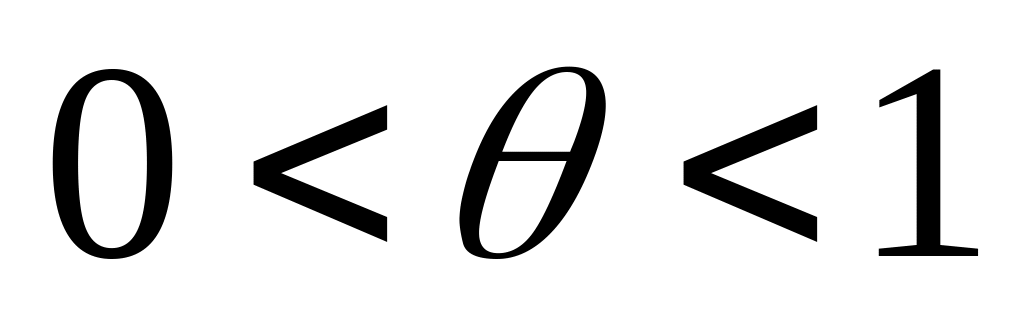 . По монотонности
будет
. По монотонности
будет
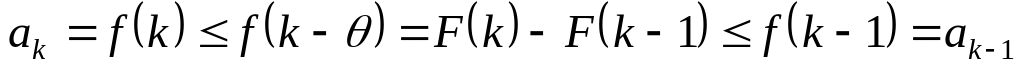 .
Отсюда видно, что если сходится
.
Отсюда видно, что если сходится
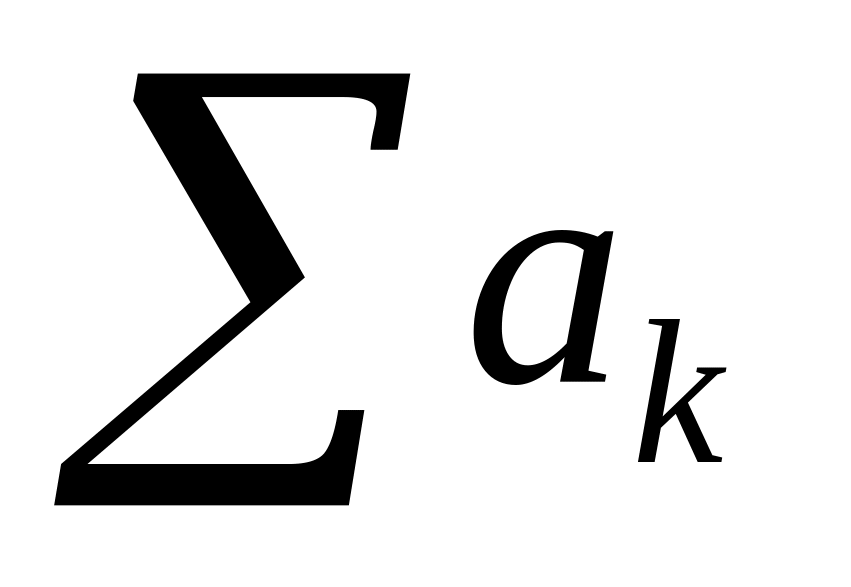 ,
то сходится
,
то сходится
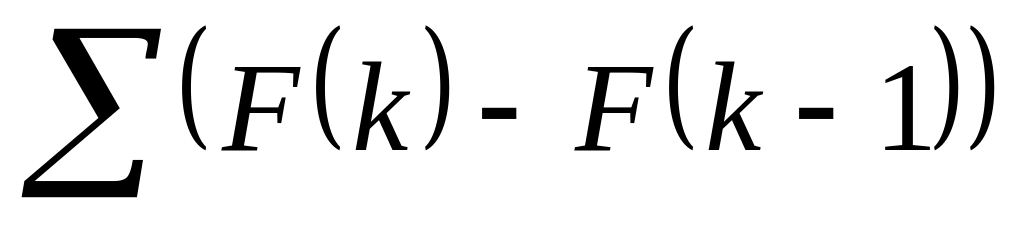 ,
и, значит, сходится
.
Обратно, если
сходится, то сходится
,
а, значит, по I признаку
сходится
.
,
и, значит, сходится
.
Обратно, если
сходится, то сходится
,
а, значит, по I признаку
сходится
.
