
- •Последовательности и их пределы
- •Подпоследовательности и частичные пределы
- •Критерий сходимости последовательности.
- •Предел функции и его свойства
- •Классификация бесконечно больших и бесконечно малых функций
- •Равномерная непрерывность функции
- •Раскрытие неопределённостей (правила Лоппиталя)
- •Исследование функций
- •Выпуклость в точке перегиба
Математический анализ
Лектор: Юрченко Александр Максимович
I семестр – осенний семестр 2002 года
Таблица эквивалентных функций (при
![]() ):
):
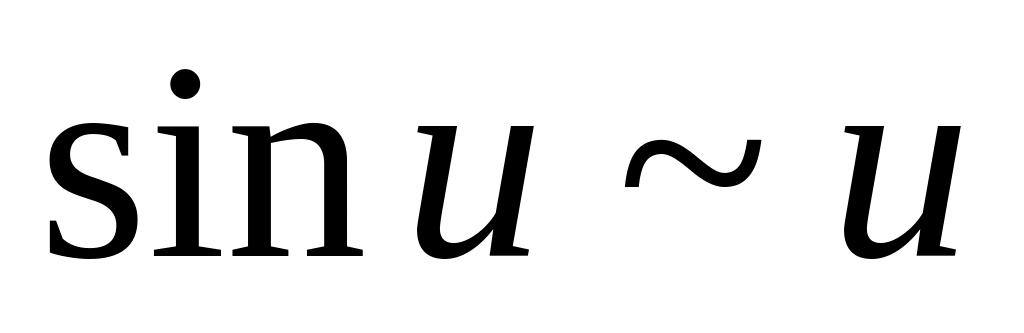 .
.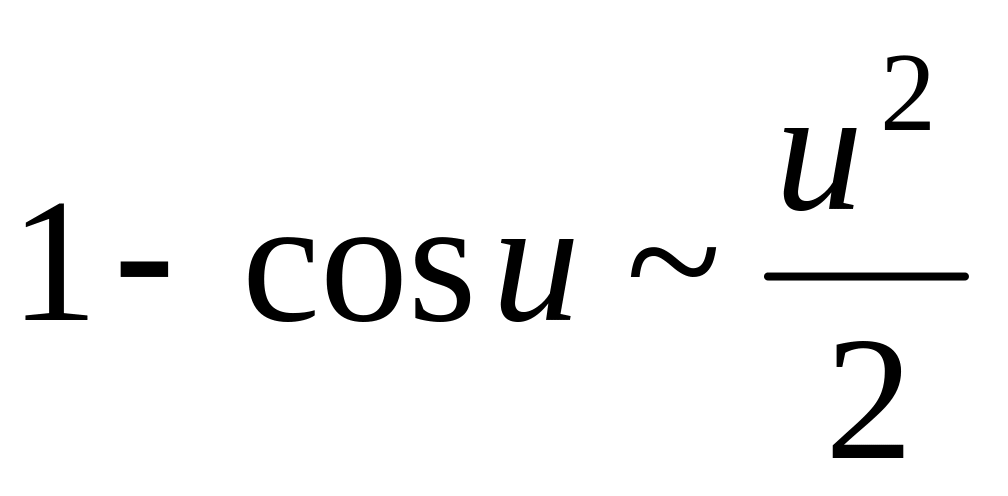 .
.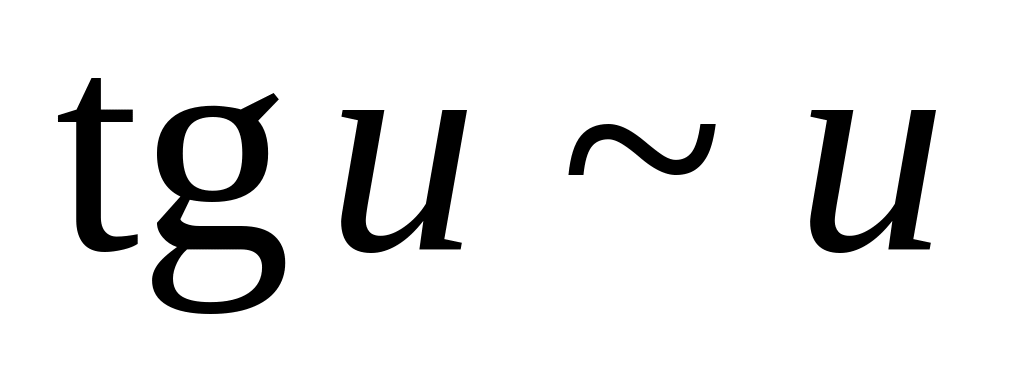 .
.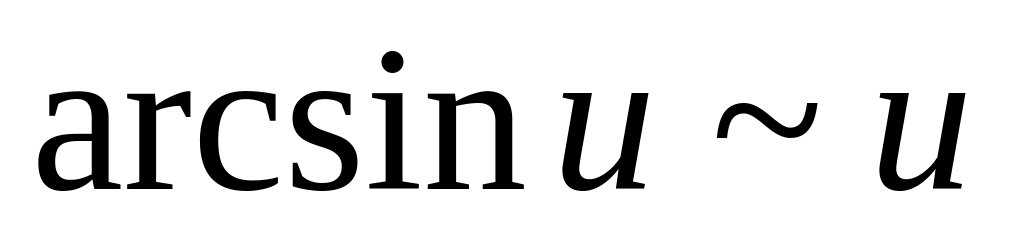 .
.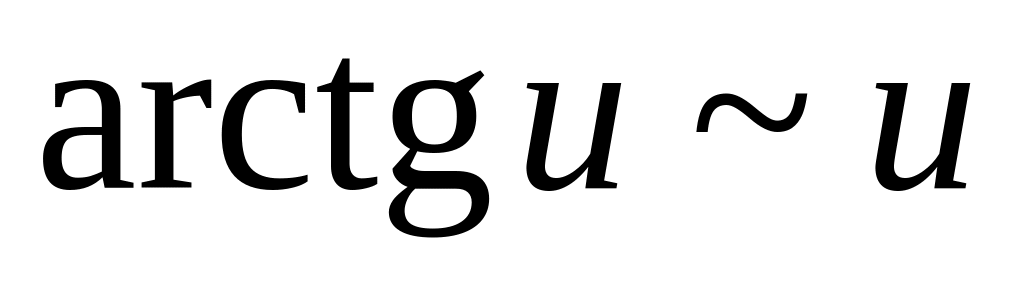 .
.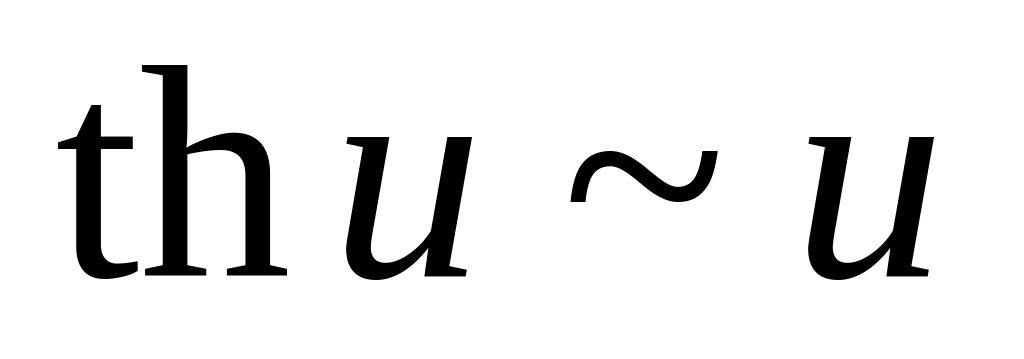 .
.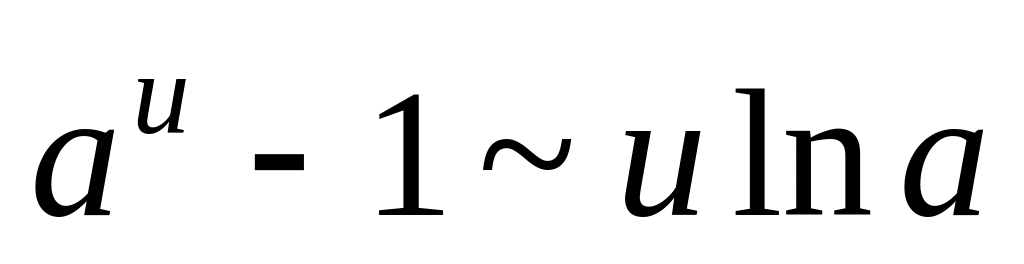 .
.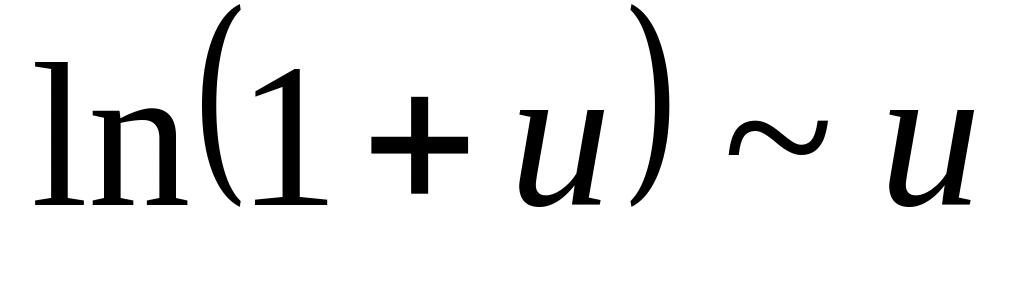 .
.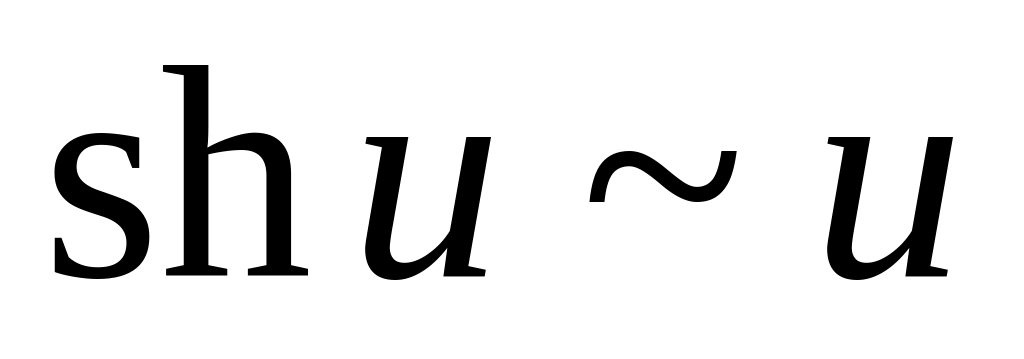 .
.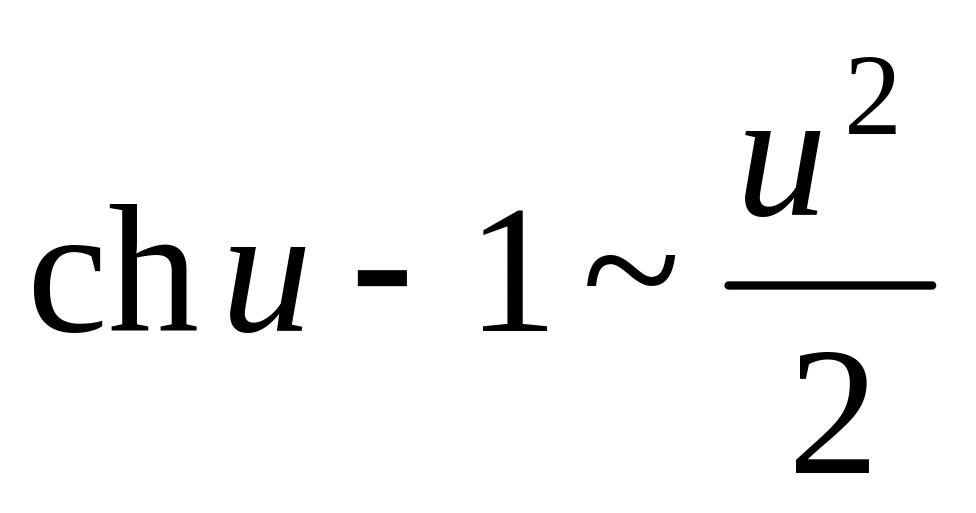 .
.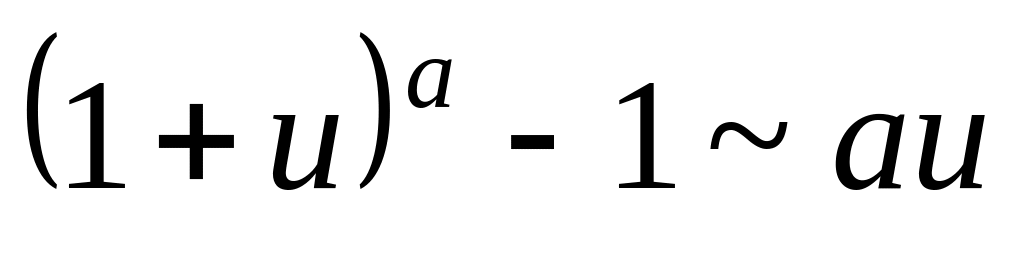 .
.
Таблица производных
|
Таблица интегралов
|
Действительные числа
Действительным числом называется бесконечная последовательность цифр с одной запятой между ними и знаком «+» или «–» перед (при этом числа с бесконечным числом нулей в периоде невозможно отличить от соответствующих чисел с бесконечным количеством девяток в периоде).
![]() и
и
![]() будут равны,
если
будут равны,
если
![]() ,
,
![]() ,
,
![]() ,
…,
,
…,
![]() и знаки совпадают.
и знаки совпадают.
Числа со
знаком «+» называются положительными,
со знаком «–» – отрицательными,
а число
![]() - нулём.
- нулём.
Неравенства: Всякое положительное число
больше нуля, всякое отрицательное –
меньше. Пусть
![]() ,
,
![]() .
Говорят, что
.
Говорят, что
![]() ,
если либо
,
если либо
![]() ,
либо
,
а
,
либо
,
а
![]() ,
либо
,
,
а
,
либо
,
,
а
![]() и т.д. (т.е.
и т.д. (т.е.
![]() для
для
![]() ,
,
![]() ).
).
Если
,
то
![]() .
.
Если
и
отрицательны, то
,
если
![]() .
Если
.
Если
![]() ,
а
,
а
![]() ,
то
,
то
![]() .
Если
и
.
Если
и
![]() ,
то
,
то
![]() .
.
Пусть дано числовое множество A.
Число M
называется верхней
границей множества A,
если для
![]() будет выполнено условие
будет выполнено условие
![]() .
Если у A
существует верхняя граница, то A
называется ограниченным
сверху.
.
Если у A
существует верхняя граница, то A
называется ограниченным
сверху.
Пусть множество A
ограничено сверху. Наименьшая
из верхних границ называется верхней
гранью и обозначается
![]() .
.
Теорема о точной грани: Если множество A не пусто и ограничено сверху, то у него существует точная верхняя грань.
Пусть множество A не
пусто и ограничено сверху, а B
– множество всех чисел, ограничивающих
сверху множество A.
Если
![]() и
и
![]() ,
то из определения числа, ограничивающего
сверху множество, следует, что
,
то из определения числа, ограничивающего
сверху множество, следует, что
![]() .
Следовательно, существует такое число
, что для всех
a и b
будет выполняться неравенство
.
Следовательно, существует такое число
, что для всех
a и b
будет выполняться неравенство
![]() .
Неравенство
.
Неравенство
![]() ,
означает, что
ограничивает сверху множество A,
а неравенство
,
означает, что
ограничивает сверху множество A,
а неравенство
![]() ,
– что число –
наименьшее среди всех чисел, ограничивающих
сверху множество A.
Следовательно,
,
– что число –
наименьшее среди всех чисел, ограничивающих
сверху множество A.
Следовательно,
![]() .
.
Свойства абсолютных величин: для любых
a и b
выполняются неравенства
![]() ,
,
![]() .
.
Последовательности и их пределы
Последовательностью называется функция, область определения которой – совокупность натуральных чисел.
Последовательность
![]() ограничена сверху, если
ограничена сверху, если
![]() такое, что
такое, что
![]() для
для
![]() ,
снизу,
если
,
снизу,
если
![]() такое, что
такое, что
![]() для
для
![]() ,
ограничена,
если
такое,
что
,
ограничена,
если
такое,
что
![]() для
.
для
.
![]() для
для
![]() для
для
![]() будет
будет
![]() .
.
называется
бесконечно малой, если
![]() .
.
Пример:
![]() ,
т.е. для
,
т.е. для
![]() будет
будет
![]() .
.
Свойства бесконечно малой последовательности:
Бесконечно малая последовательность ограничена.
Пусть
![]() – бесконечно малая. Тогда
– бесконечно малая. Тогда
![]() для
будет
для
будет
![]() .
Введём
.
Введём
![]()
![]() .
Тогда для
.
Тогда для
![]() будет
будет
![]() .
Следовательно,
ограничена.
.
Следовательно,
ограничена.
Сумма любого конечного числа бесконечно малых будет бесконечно малой.
Сначала докажем для двух бесконечно
малых. Пусть
и
![]() – бесконечно малые.
Возьмём
– бесконечно малые.
Возьмём
![]() .
Тогда
.
Тогда
![]() и
и
![]() такие, что для
такие, что для
![]() будет
будет
![]() и
и
![]() будет
будет
![]() .
Введём
.
Введём
![]() .
Тогда для
будет
.
Тогда для
будет
![]() .
Следовательно,
.
Следовательно,
![]() – бесконечно малая.
– бесконечно малая.
Аналогично
![]() и т.д.
и т.д.
Разность бесконечно малых будет бесконечно малая.
Следует из того, что
![]() и, следовательно, для тех же
и N, что и в прошлой
теореме, будет
и, следовательно, для тех же
и N, что и в прошлой
теореме, будет
![]() для
.
для
.
Произведение ограниченной последовательности на бесконечно малую будет бесконечно малая.
Пусть
– бесконечно малая, а
![]() – ограниченная. Тогда
– ограниченная. Тогда
![]() такое, что
(следует из определения ограниченности).
Возьмём
.
Тогда, т.к.
– бесконечно малая, то
для
будет
такое, что
(следует из определения ограниченности).
Возьмём
.
Тогда, т.к.
– бесконечно малая, то
для
будет
![]() .
Тогда для
будет и
.
Тогда для
будет и
![]() .
Следовательно,
.
Следовательно,
![]() – бесконечно малая.
– бесконечно малая.
Если – бесконечно малая и
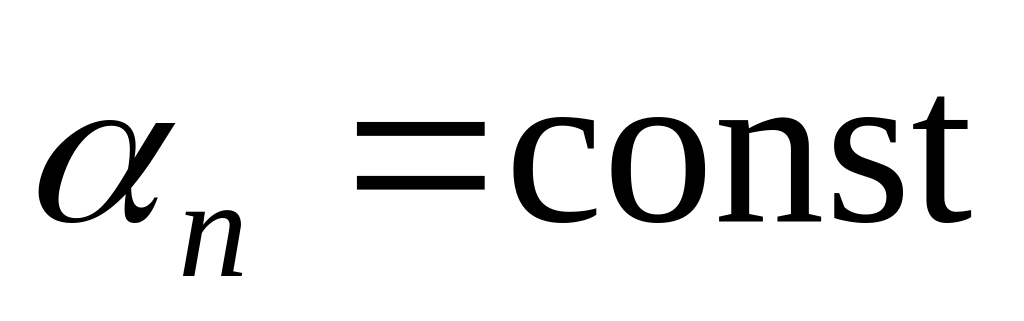 ,
то
,
то
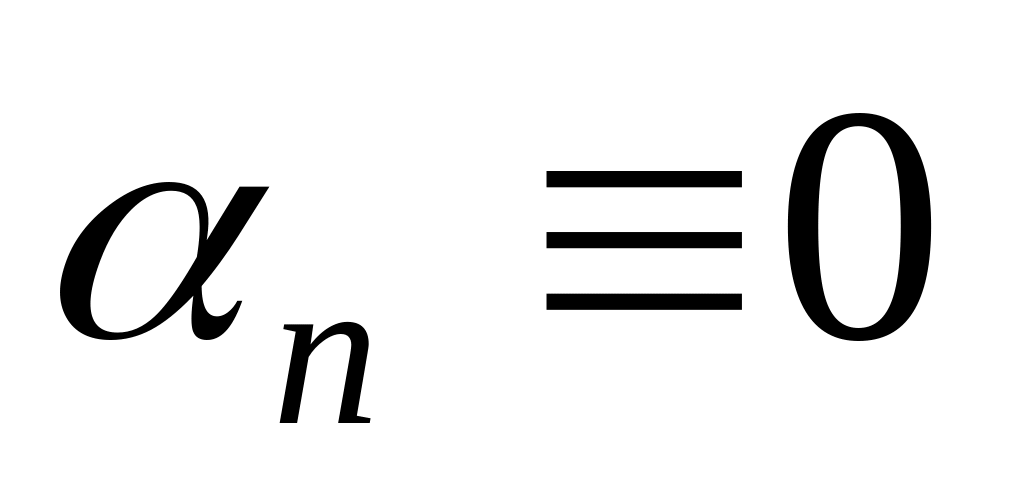 .
.
Пусть
и
![]() .
Возьмём
.
Возьмём
![]() .
Тогда, по определению бесконечно малой
для
будет
.
Тогда, по определению бесконечно малой
для
будет
![]() ,
т.е.
,
т.е.
![]() или
или
![]() ,
что невозможно. Полученное противоречие
доказывает теорему.
,
что невозможно. Полученное противоречие
доказывает теорему.
называется
бесконечно большой,
если
![]() ,
т.е. для
,
т.е. для
![]() для
будет
для
будет
![]() .
.
Если
– бесконечно большая, то хотя бы с
некоторого n
определена последовательность
![]() и эта последовательность бесконечно
малая.
и эта последовательность бесконечно
малая.
Возьмём, например,
 .
Тогда
.
Тогда
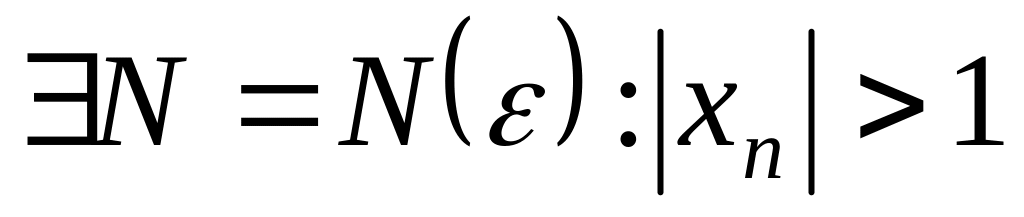 для
для
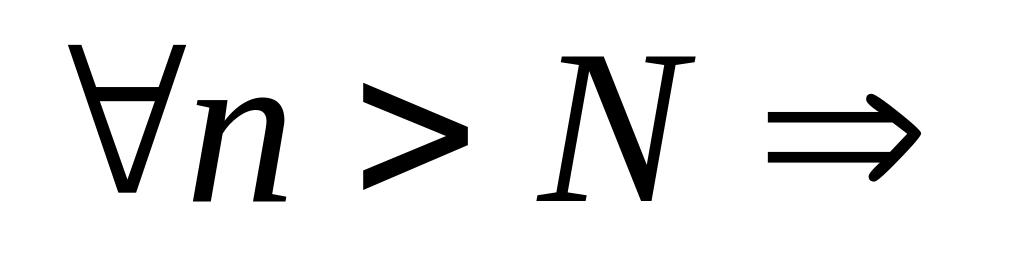 для
определена.
для
определена.Возьмём . Тогда, т.к. – бесконечно большая, то для будет . Тогда для будет
 – бесконечно малая.
– бесконечно малая.
Число является пределом для последовательности, если вне её сколь угодно малой окрестности лежит конечное число членов последовательности.
Если
![]() ,
то
,
то
![]() .
.
Возьмём
.
Тогда
для
будет
![]() .
.
![]() тогда и только тогда, когда существует
бесконечно малая
такая, что
тогда и только тогда, когда существует
бесконечно малая
такая, что
![]() .
.
Теорема о единственности предела
последовательности: Если
и
![]() ,
то
,
то
![]() .
.
Пусть
и
.
Тогда существуют бесконечно малые
и
![]() и
и
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() (при
),
(при
),
![]() .
.
Сходящаяся последовательность ограничена.
Т.к.
![]() ,
то
,
где
– бесконечно малая. Но бесконечно малая
ограничена, т.е.
такое,
что
для
,
то
,
где
– бесконечно малая. Но бесконечно малая
ограничена, т.е.
такое,
что
для
![]() .
.
Если
![]() ,
то хотя бы с некоторого n
,
то хотя бы с некоторого n
![]() определена и ограничена.
определена и ограничена.
Т.к.
![]() ,
то
,
то
![]() .
Возьмём
.
Возьмём
![]() .
Тогда, т.к.
,
то
.
Тогда, т.к.
,
то
![]() такое, что для
будет
такое, что для
будет
![]() ,
т.е.
,
т.е.
![]() .
Отсюда при всех
.
Отсюда при всех
![]() будет определена
и
будет определена
и
![]() .
.
Если
и
![]() ,
то и все
,
то и все
![]() ,
начиная с некоторого n.
,
начиная с некоторого n.
Возьмём
![]() .
Тогда
при
.
Тогда
при
![]() ,
т.е.
,
т.е.
![]() .
.
Если
![]() хотя бы с некоторого номера и
,
то
.
хотя бы с некоторого номера и
,
то
.
Пусть
![]() .
Тогда
.
Тогда
![]() для
будет
для
будет
![]() – противоречие.
– противоречие.
При предельном переходе
неравенство может превратиться в
равенство. Пример:
![]() ,
.
,
.
Если
![]() и
и
![]() ,
то
,
то
![]() .
.
В формулировке теоремы
достаточно, чтобы неравенство
![]() выполнялось, начиная с некоторого
номера.
выполнялось, начиная с некоторого
номера.
Если
![]() и существуют конечные
и существуют конечные
![]() и
и
![]() ,
то
,
то
![]() .
.
Так как
,
то
![]() и
и
![]() .
По теореме
.
По теореме
![]() ,
т.е.
,
т.е.
![]() ,
откуда
,
откуда
![]() .
.
Теорема о зажатой переменной: Пусть
для
,
начиная с некоторого, будет
![]() и
и
![]() .
Тогда
.
Тогда
![]() .
.
Пусть
![]() – это такое число, что для
будет
.
Возьмём
.
Т.к.
,
то
– это такое число, что для
будет
.
Возьмём
.
Т.к.
,
то
![]() для
будет
для
будет
![]() .
Аналогично, т.к.
.
Аналогично, т.к.
![]() ,
то
,
то
![]() для
для
![]() будет
будет
![]() .
Обозначим
.
Обозначим
![]() .
Тогда для
будут выполнены все три двойных
неравенства:
.
Тогда для
будут выполнены все три двойных
неравенства:
![]() ,
т.е.
,
т.е.
![]() или
или
![]() ,
что равносильно
,
что равносильно
![]() ,
ч.т.д.
,
ч.т.д.
Арифметические операции над сходящимися последовательностями
Пусть существуют конечные и . Тогда существуют пределы:
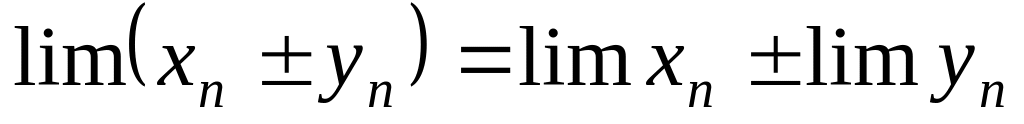 .
.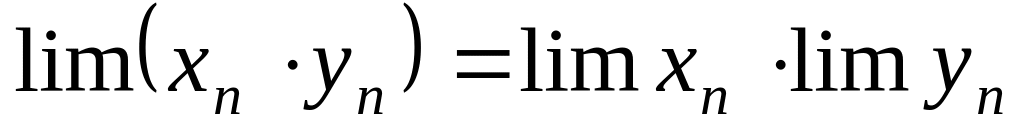 .
.Если
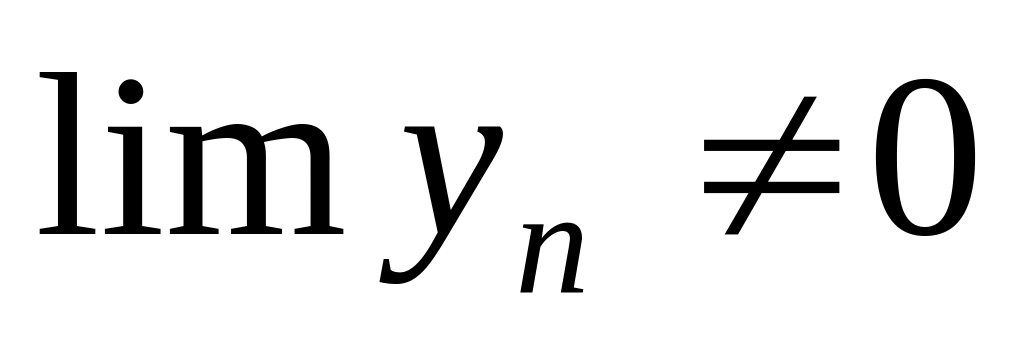 ,
то
,
то
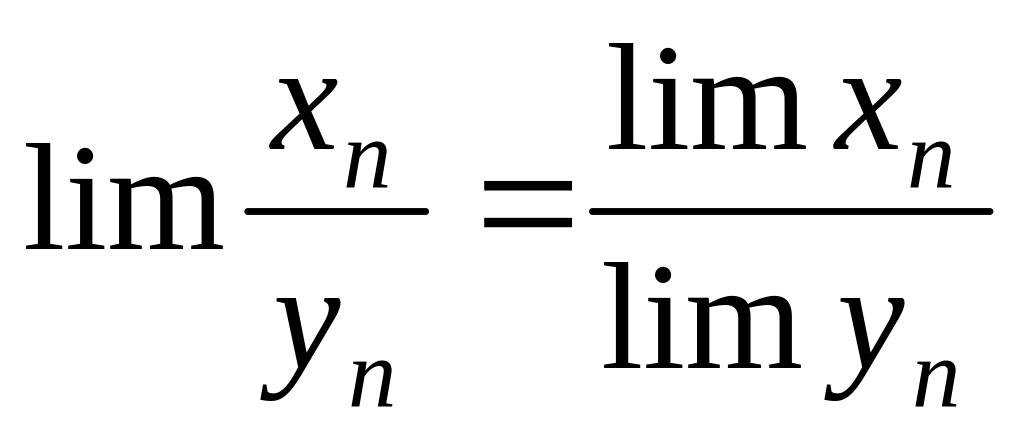 .
.
Пусть
,
а
![]() .
Тогда
,
.
Тогда
,
![]() ,
где
и
– бесконечно малые.
,
где
и
– бесконечно малые.
 ,
откуда
,
откуда
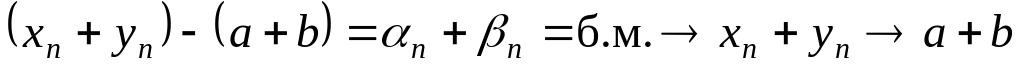 ,
т.е.
,
т.е.
 .
.Аналогично
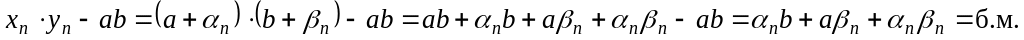
 .
. .
.
Монотонные последовательности и их пределы
Последовательность
называется неубывающей,
если для
будет
![]() ;
возрастающей,
если для
будет
;
возрастающей,
если для
будет
![]() .
.
Всякая неубывающая последовательность ограничена снизу, всякая невозрастающая – сверху.
Если неубывающая последовательность ограничена сверху, то она имеет конечный предел
Пусть
не убывает и ограничена сверху. Тогда
по теореме о точной грани существует
конечный
![]() .
Докажем, что
.
Докажем, что
![]() .
Возьмём
.
По определению
.
Возьмём
.
По определению
![]() .
Тогда для
будет
.
Тогда для
будет
![]() .
Следовательно, для
будет
,
т.е.
.
.
Следовательно, для
будет
,
т.е.
.
Для справедливости теоремы достаточна монотонность, начинающаяся с некоторого номера.
Если
не убывает и не ограничена сверху, то
![]() .
.
Возьмём
.
Т.к.
не ограничена сверху, то
![]() ,
т.е.
,
т.е.
![]() для
для
![]() .
.
Критерий сходимости монотонной последовательности: Монотонная последовательность имеет предел тогда и только тогда, когда она ограничена.
Существует конечный предел
последовательности
![]() .
Этот предел называется числом e
и он равен 2.71828182845905…
.
Этот предел называется числом e
и он равен 2.71828182845905…
Используем формулу бинома Ньютона:
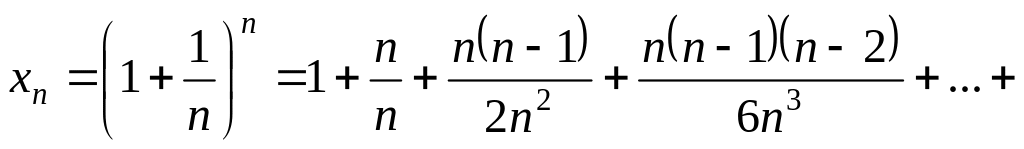
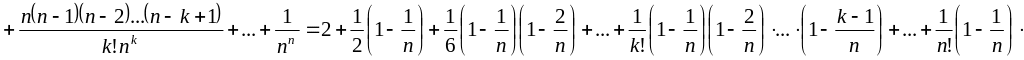
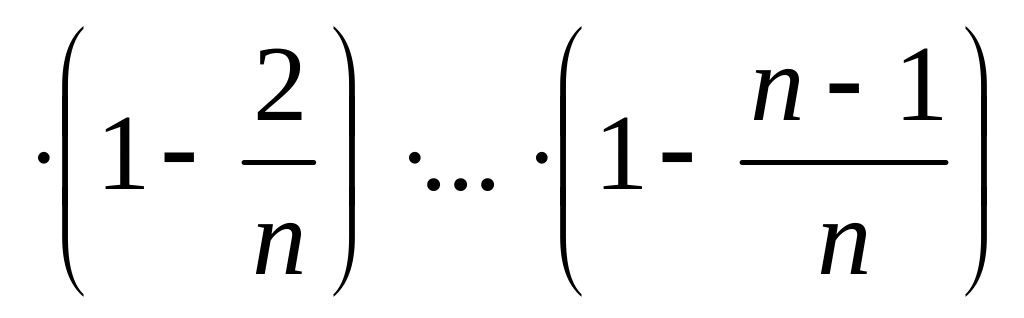 .
.
Покажем, что возрастает. Напишем
 и сравним с
:
и сравним с
:
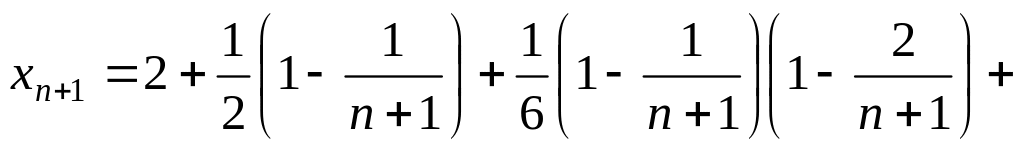
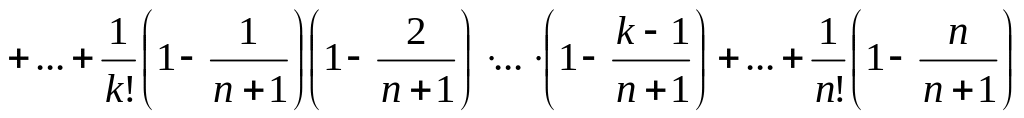 .
В
каждое слагаемое больше, чем в
,
т.к.
.
В
каждое слагаемое больше, чем в
,
т.к.
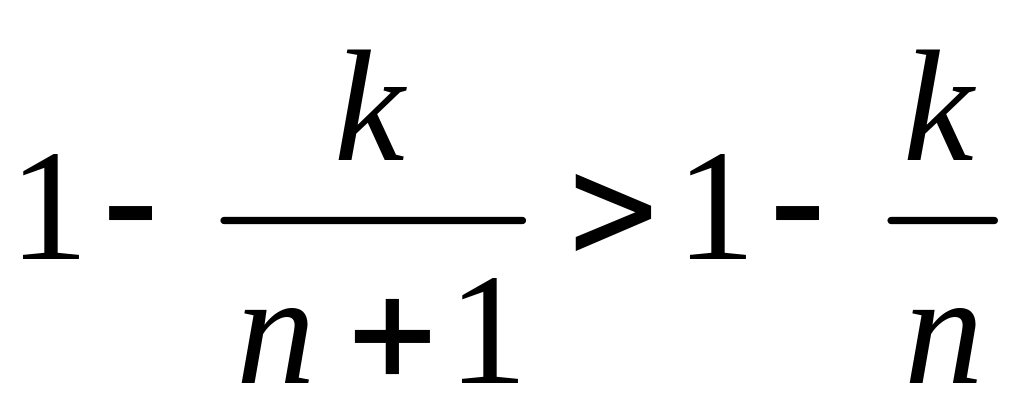 и в
есть лишнее положительное слагаемое.
Следовательно,
и в
есть лишнее положительное слагаемое.
Следовательно,
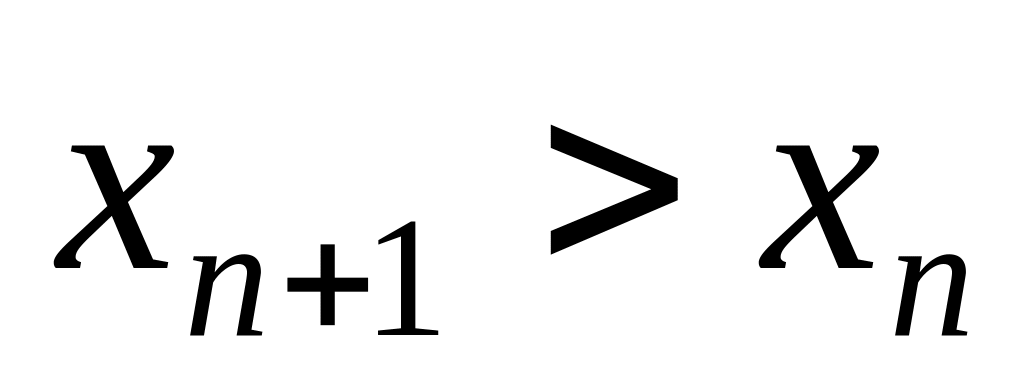 .
.Покажем, что ограничена сверху:
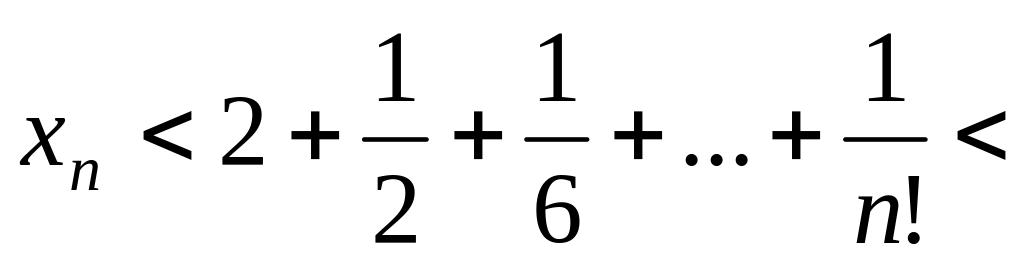 (т.к.
(т.к.
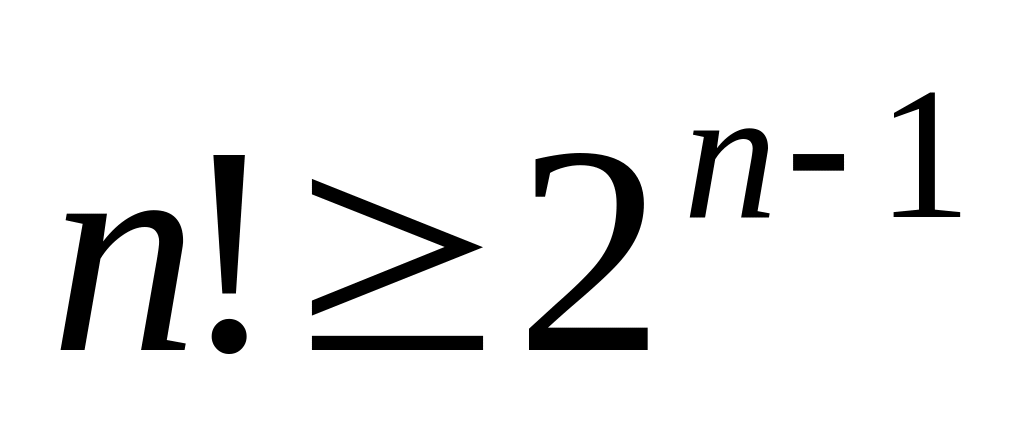 )
)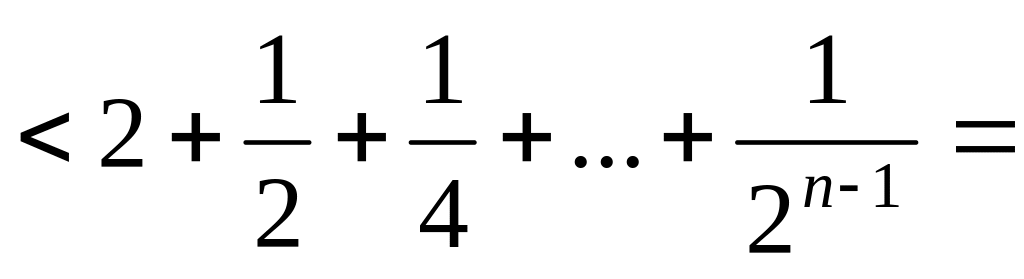 (геометрическая прогрессия)
(геометрическая прогрессия)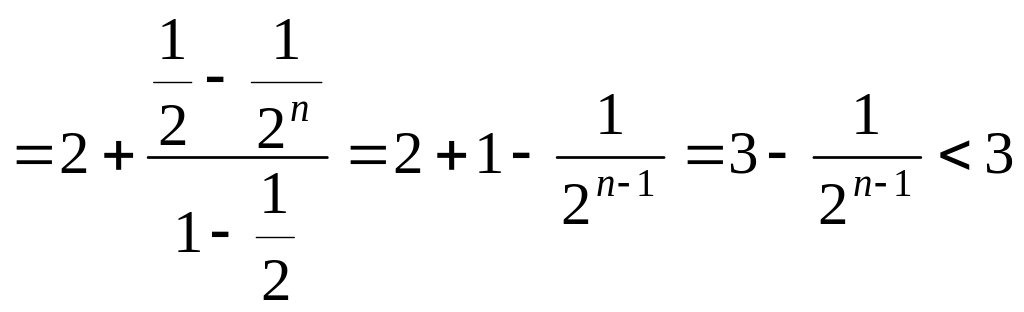 .
.Отсюда, т.к.
 и
и
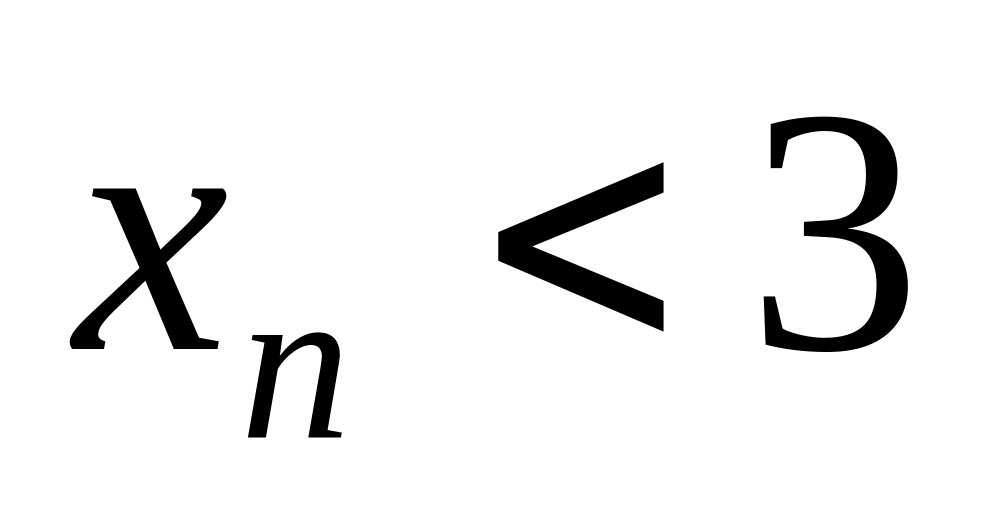 ,
то существует конечный
.
Видно, что
,
то существует конечный
.
Видно, что
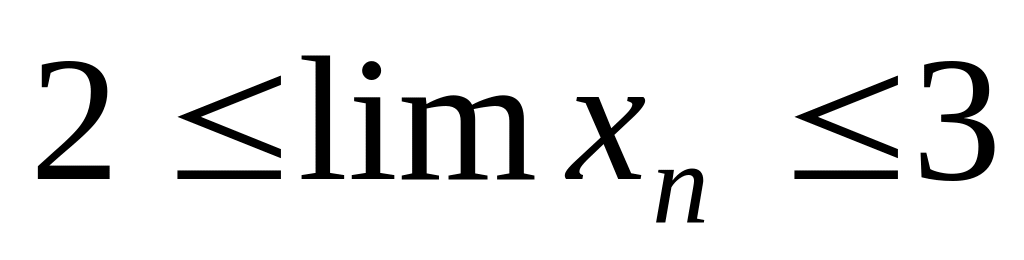 .
.
Теорема о вложенных отрезках: Пусть
дана последовательность вложенных
отрезков
![]()
![]() ,
причём длина
,
причём длина
![]() при
при
![]() .
Тогда существует единственная точка
.
Тогда существует единственная точка
![]() для
и
для
и
![]() .
.
Докажем, что точка C существует. Заметим, что
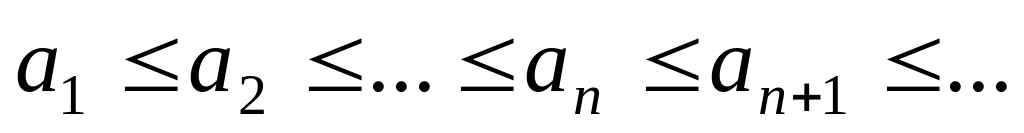 ,
т.е.
,
т.е.
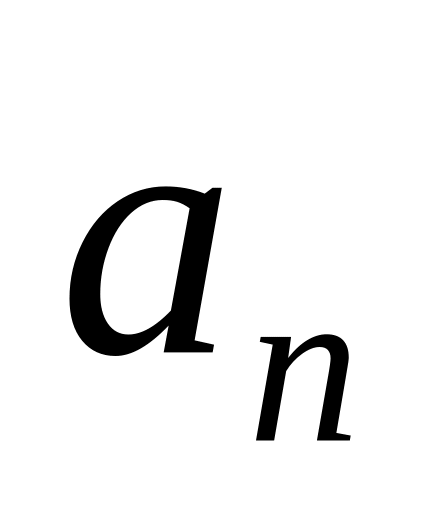 не убывает. Кроме того,
не убывает. Кроме того,
 для
,
т.е.
для
,
т.е.
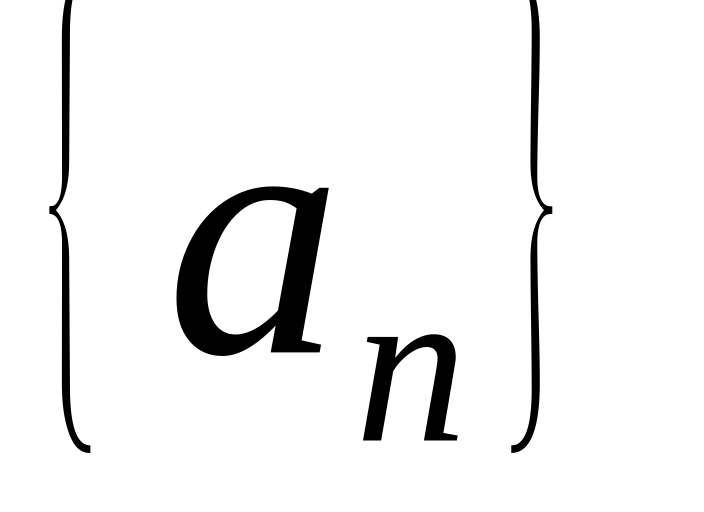 ограничена сверху числом
ограничена сверху числом
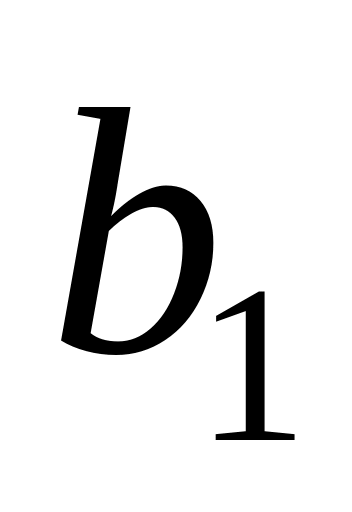 .
По теореме об ограниченной
последовательности,
.
По теореме об ограниченной
последовательности,
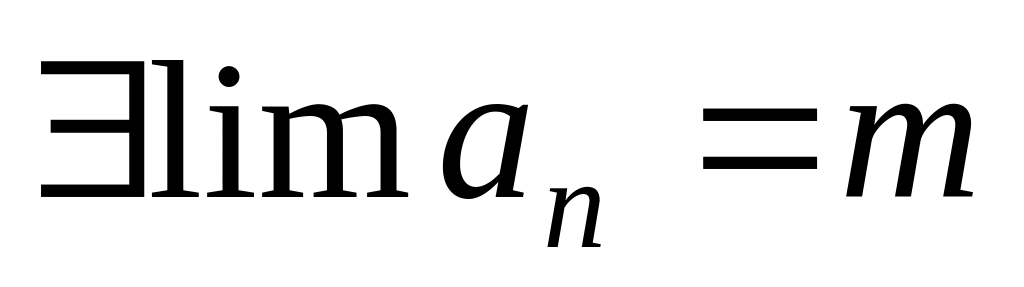 .
Т.к.
.
Т.к.
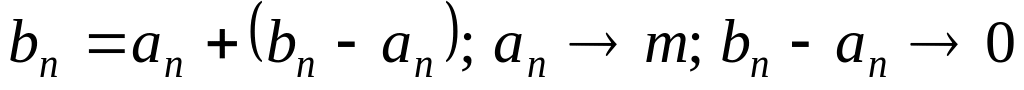 ,
то
,
то
 .
При этом
.
При этом
 ,
т.е.
,
т.е.
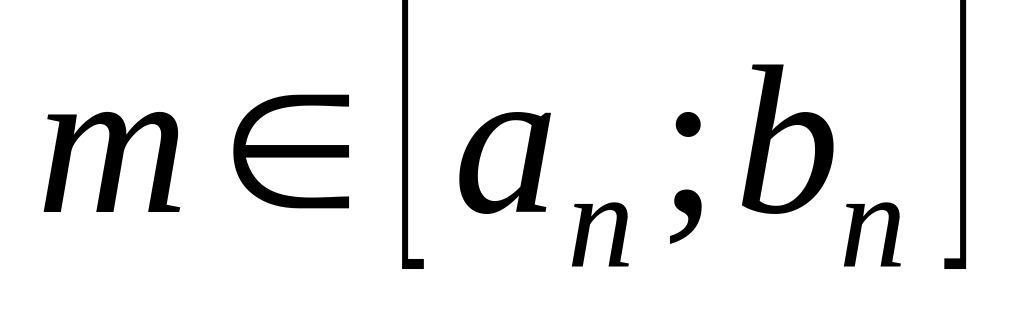 для
для
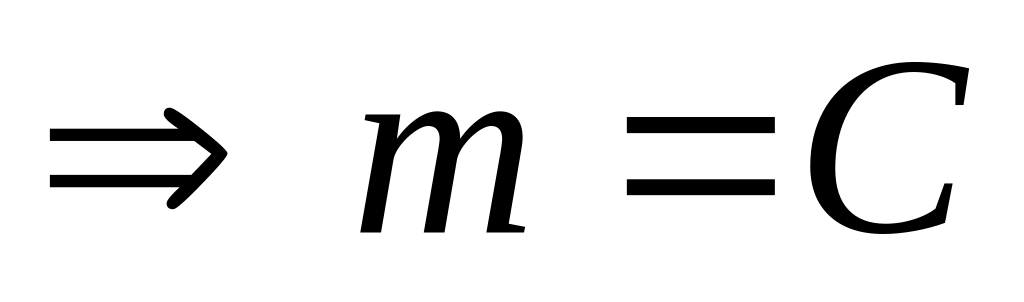 .
.Докажем, что C – единственная точка. Пусть существует другая точка
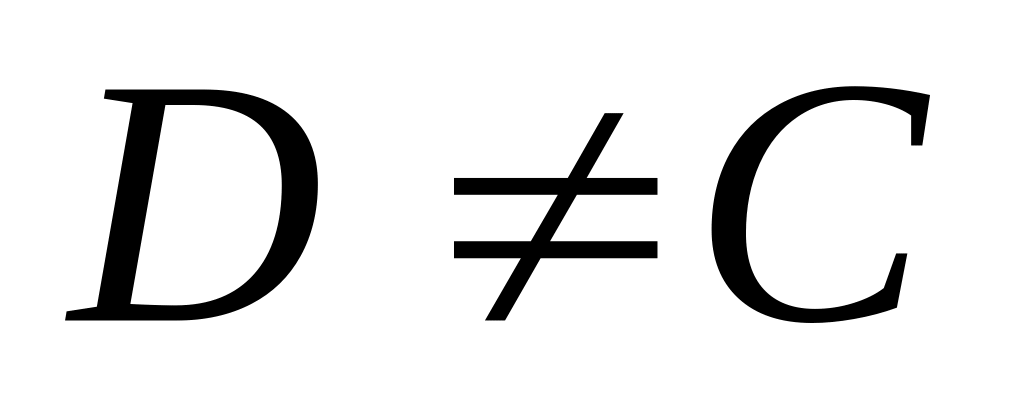 ,
которая принадлежит отрезку
,
которая принадлежит отрезку
 при
.
Тогда
при
.
Тогда
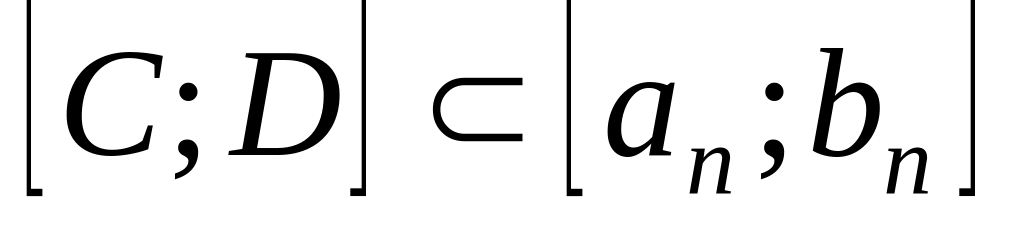 для
.
Значит, для
длина
для
.
Значит, для
длина
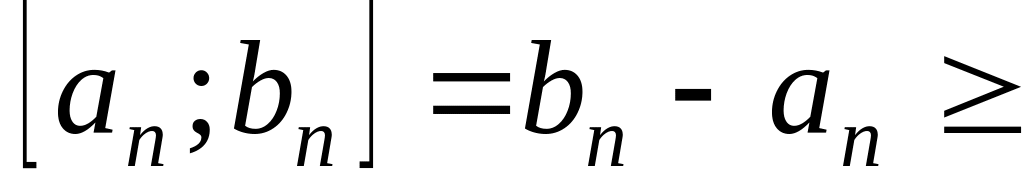 длины
длины
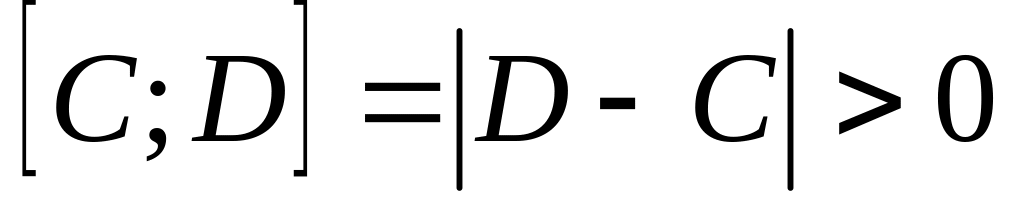 .
Поэтому не может длина
,
что противоречит условию.
.
Поэтому не может длина
,
что противоречит условию.
