
- •Последовательности и их пределы
- •Подпоследовательности и частичные пределы
- •Критерий сходимости последовательности.
- •Предел функции и его свойства
- •Классификация бесконечно больших и бесконечно малых функций
- •Равномерная непрерывность функции
- •Раскрытие неопределённостей (правила Лоппиталя)
- •Исследование функций
- •Выпуклость в точке перегиба
Классификация бесконечно больших и бесконечно малых функций
Пусть
![]() и
и
![]() обе бесконечно большие или бесконечно
малые при
обе бесконечно большие или бесконечно
малые при
![]() .
Тогда говорят, что
.
Тогда говорят, что ![]() есть
есть
![]() при
,
если
при
,
если
![]() .
В этом случае также говорят, что
– бесконечно малая
более высокого порядка, чем
.
.
В этом случае также говорят, что
– бесконечно малая
более высокого порядка, чем
.
Свойства:
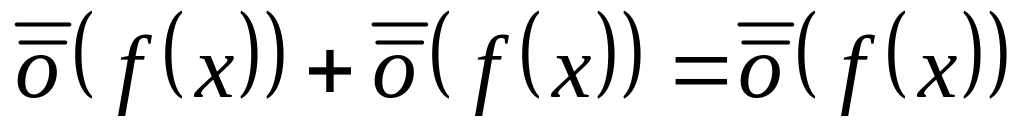 .
.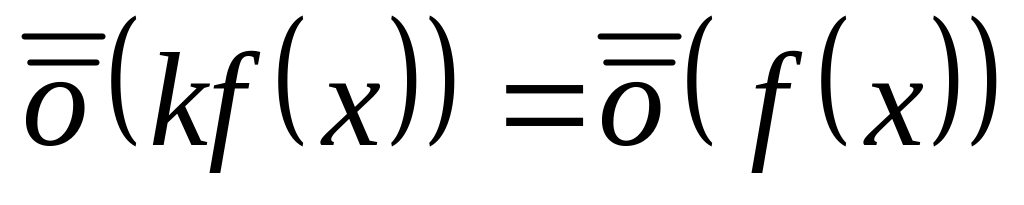 ,
где
,
где
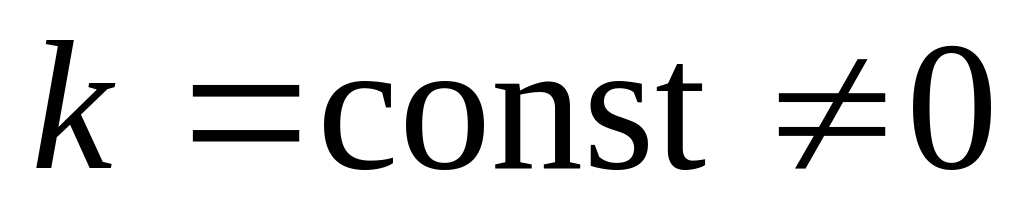 .
.
Доказательства:
Имеем
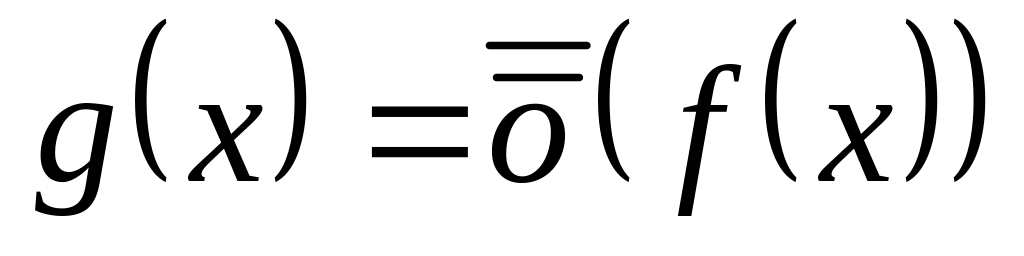 и
и
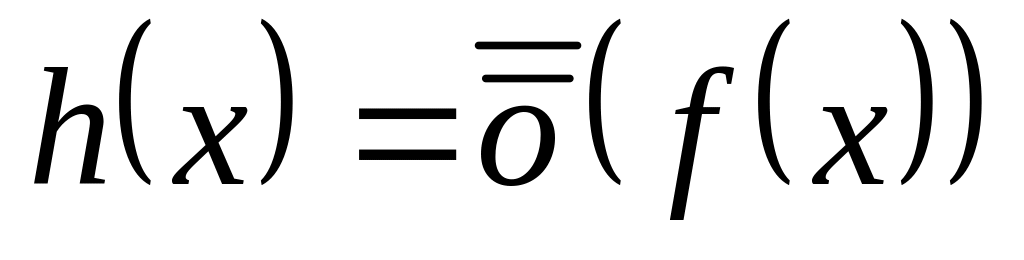 при
,
т.е.
при
,
т.е.
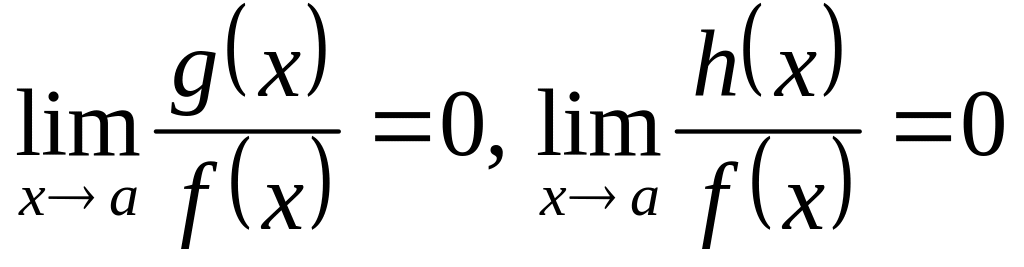 .
Отсюда
.
Отсюда
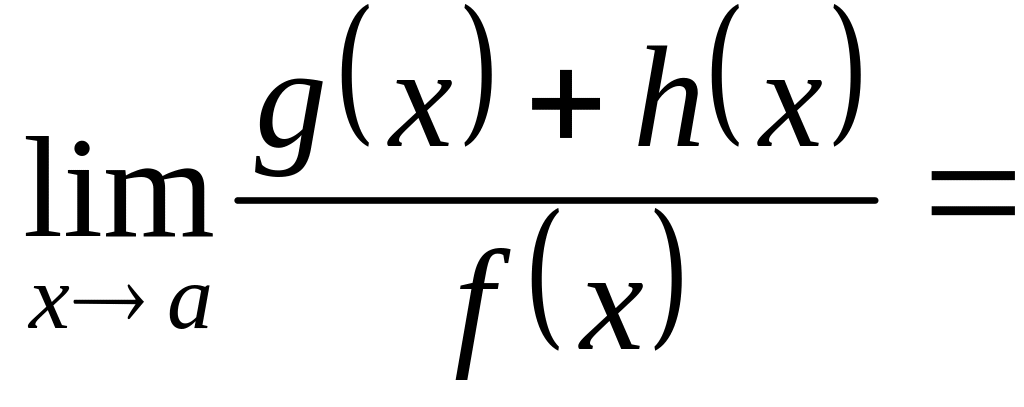
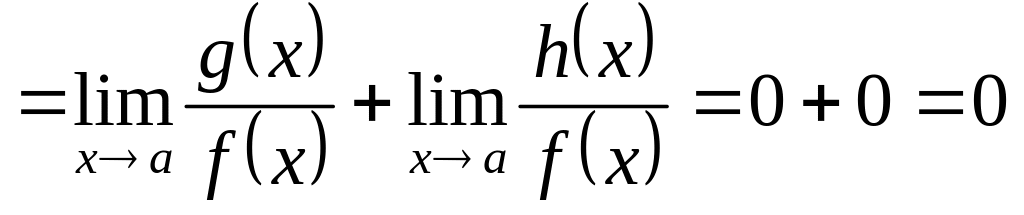 ,
т.е.
,
т.е.
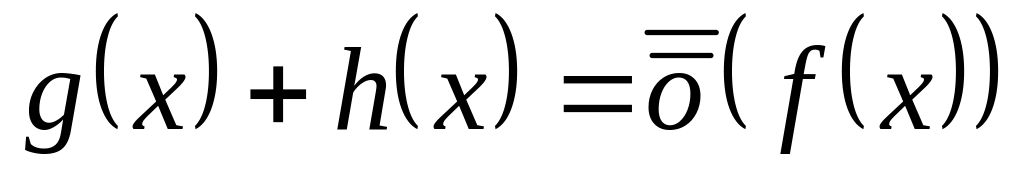 при
.
при
.Пусть
 при
,
т.е.
при
,
т.е.
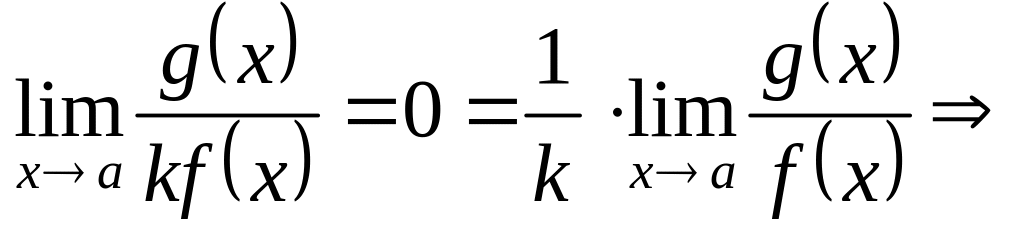 (т.к.
(т.к.
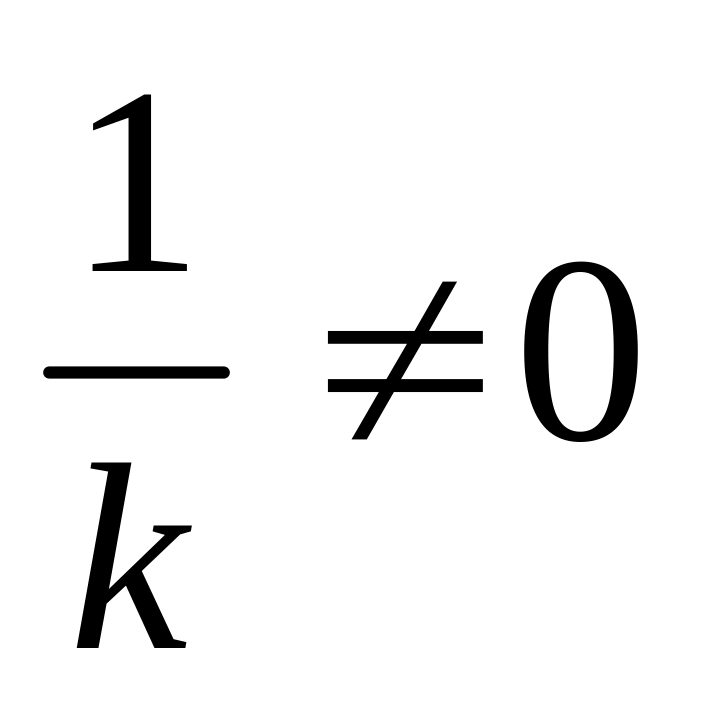 )
)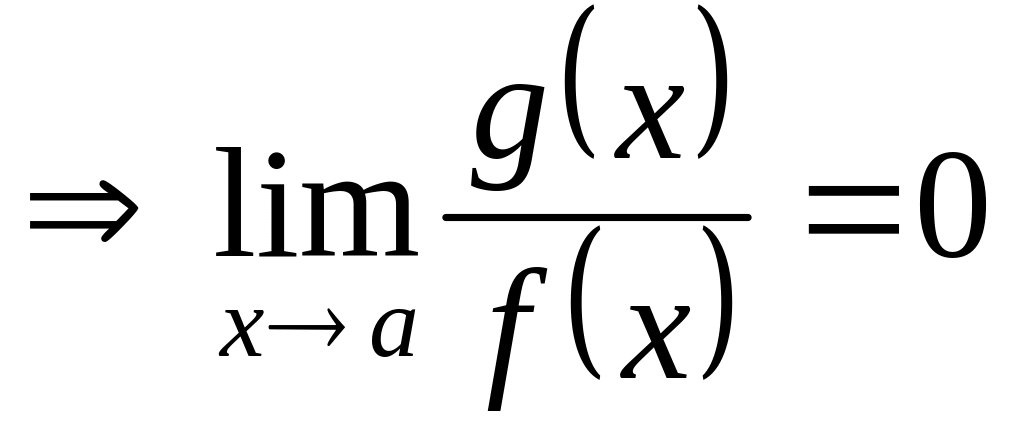 ,
т.е.
.
,
т.е.
.
![]() (
эквивалентно
)
при
означает, что
и
обе либо бесконечно малые, либо бесконечно
большие и
(
эквивалентно
)
при
означает, что
и
обе либо бесконечно малые, либо бесконечно
большие и
![]() .
.
при
тогда и только тогда, когда
![]() .
.
Пусть при . Т.е.
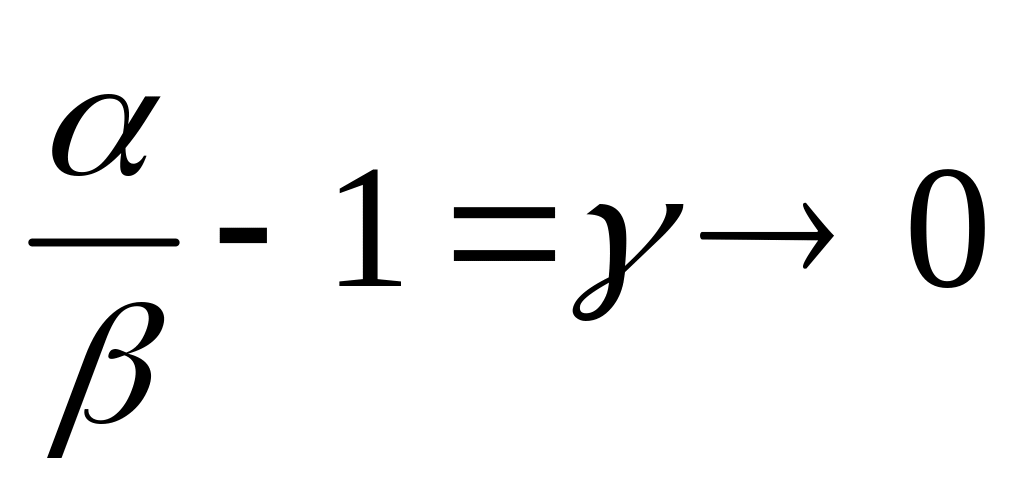 при
.
Отсюда
при
.
Отсюда
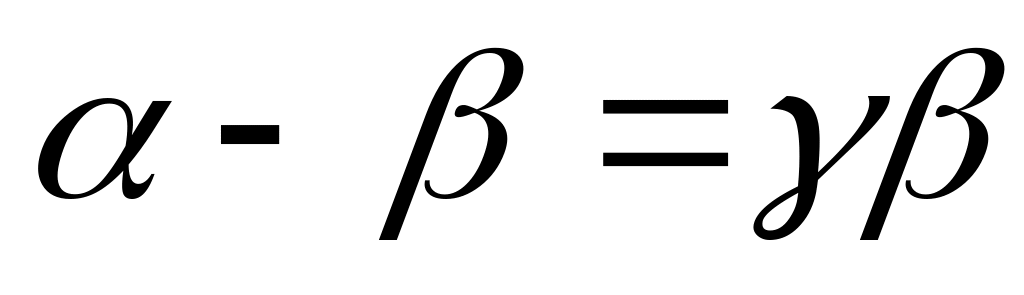 и, следовательно,
и, следовательно,
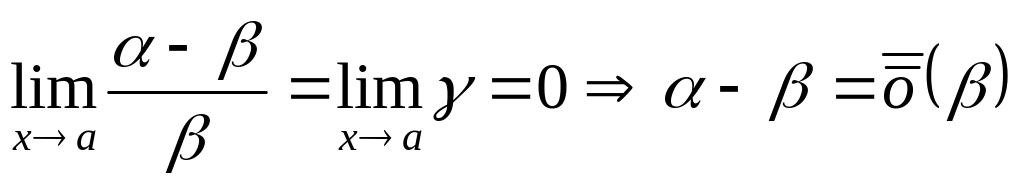 .
Возьмём теперь
.
Возьмём теперь
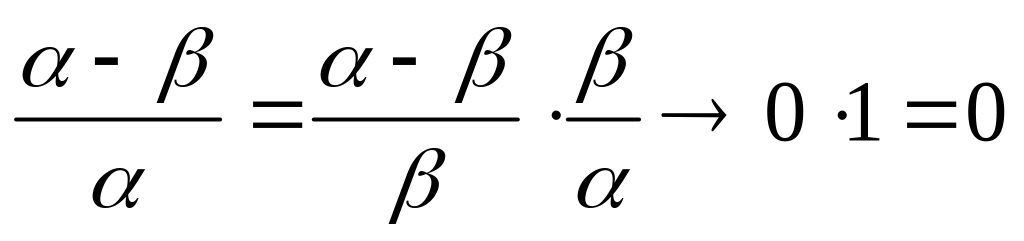 ,
т.е.
,
т.е.
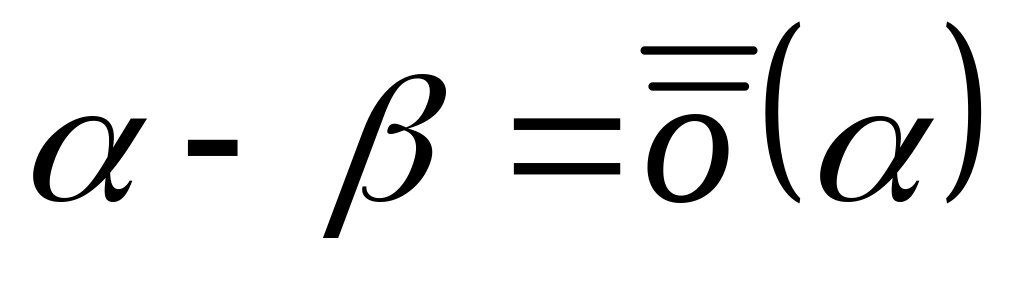 .
.Пусть теперь
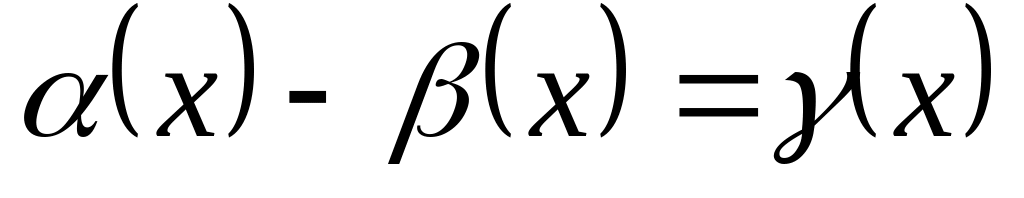 ,
где
,
где
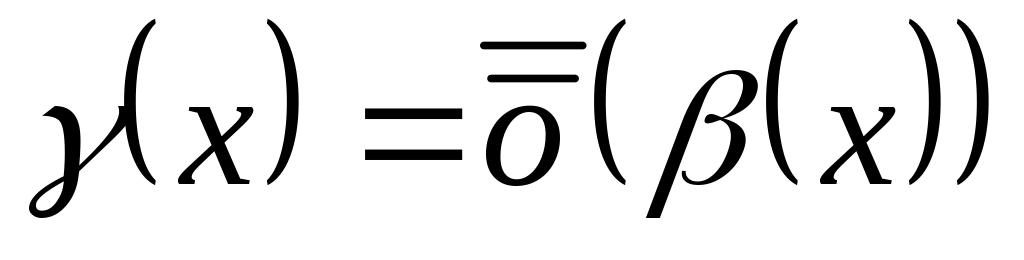 при
.
Отсюда
при
.
Отсюда
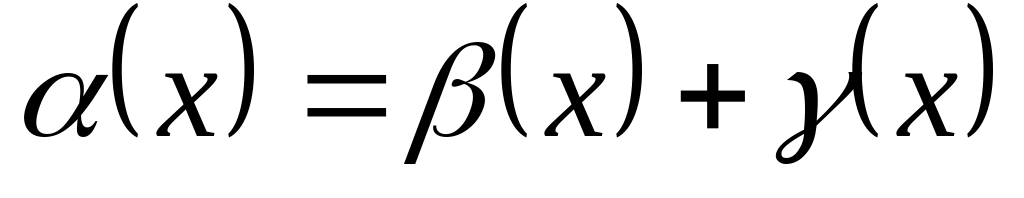 и
и
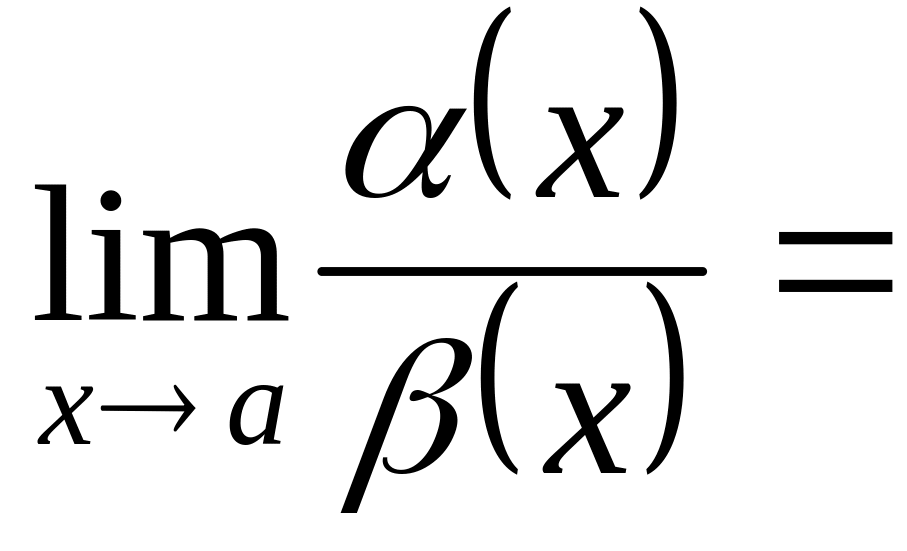
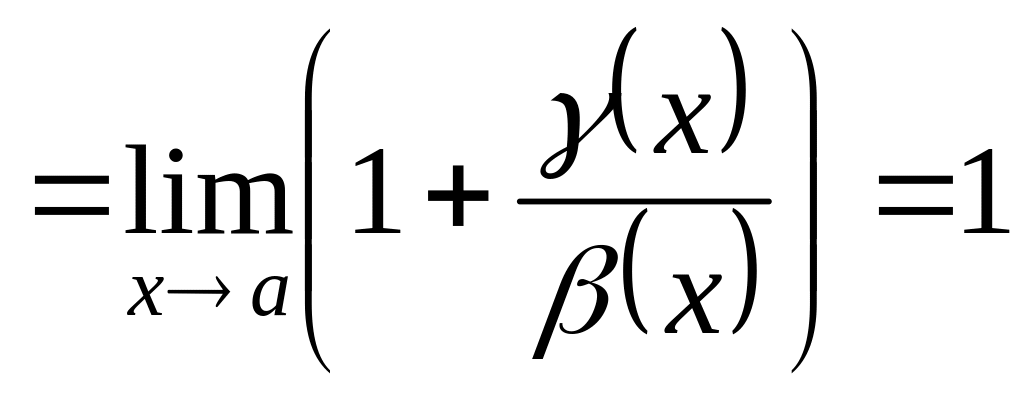 .
.
Говорят, что выражение вида
![]() является главной частью
при
,
если
является главной частью
при
,
если
![]() и
– бесконечно малые и если
и
– бесконечно малые и если
![]() при
.
при
.
I теорема Коши:
Если
определена на
и
![]() ,
то существует точка
,
то существует точка
![]() .
.
Поделим промежуток
пополам точкой
.
Если
![]() ,
то
,
то
![]() и теорема доказана. Иначе, если
и теорема доказана. Иначе, если
![]() ,
то обозначим
,
то обозначим
![]() ,
а если
,
а если
![]() ,
то
,
то
![]() .
Поделим промежуток
пополам точкой
.
Поделим промежуток
пополам точкой
![]() и повторим операцию. Таким образом, мы
либо через конечное число шагов наткнёмся
на точку
и повторим операцию. Таким образом, мы
либо через конечное число шагов наткнёмся
на точку
![]() ,
либо получим систему вложенных отрезков:
,
либо получим систему вложенных отрезков:
![]()
![]() ,
при этом длина
,
при этом длина
![]() при
.
Тогда по теореме о вложенных отрезках,
существует точка
для
и
.
При этом
при
.
Тогда по теореме о вложенных отрезках,
существует точка
для
и
.
При этом
![]() ,
а
,
а
![]() .
Следовательно,
.
Следовательно,![]() и
и
![]() .
Тогда
.
Тогда
![]() .
.
II теорема Коши:
Пусть
непрерывна на
![]() .
Тогда для
.
Тогда для
![]()
![]() .
.
Введём вспомогательную функцию
![]() .
Тогда
.
Тогда
![]() ,
,
![]() ,
причём
,
причём
![]() и
непрерывна. Тогда по I
теореме Коши
и
непрерывна. Тогда по I
теореме Коши
![]() ,
т.е.
,
т.е.
![]() или
или
![]() .
.
Пусть функция определена
в некоторой окрестности точки
![]() ,
кроме, возможно, самой точки
.
Тогда
называется точкой
разрыва функции, если
функция не определена в самой точке
,
или если она определена в этой точке,
но не является в ней непрерывной.
,
кроме, возможно, самой точки
.
Тогда
называется точкой
разрыва функции, если
функция не определена в самой точке
,
или если она определена в этой точке,
но не является в ней непрерывной.
Если
– точка разрыва функции
и существуют конечные пределы
![]() и
и
![]() ,
то точка
называют точкой разрыва
первого рода, а величину
,
то точка
называют точкой разрыва
первого рода, а величину
![]() – скачком функции в точке
.
– скачком функции в точке
.
Если скачок функции в точке равен нулю, то точку называют точкой устранимого разрыва.
Все остальные разрывы относятся к разрывам второго рода.
Теорема об обратной функции: Пусть
на некотором промежутке X
![]() строго возрастает (убывает) и непрерывна.
Тогда на соответствующем промежутке Y
может быть определена обратная функция
строго возрастает (убывает) и непрерывна.
Тогда на соответствующем промежутке Y
может быть определена обратная функция
![]() ,
которая на Y
тоже возрастает (убывает) и непрерывна.
,
которая на Y
тоже возрастает (убывает) и непрерывна.
Пусть, например, возрастает. Её значения сплошь заполняют промежуток Y. Возьмём
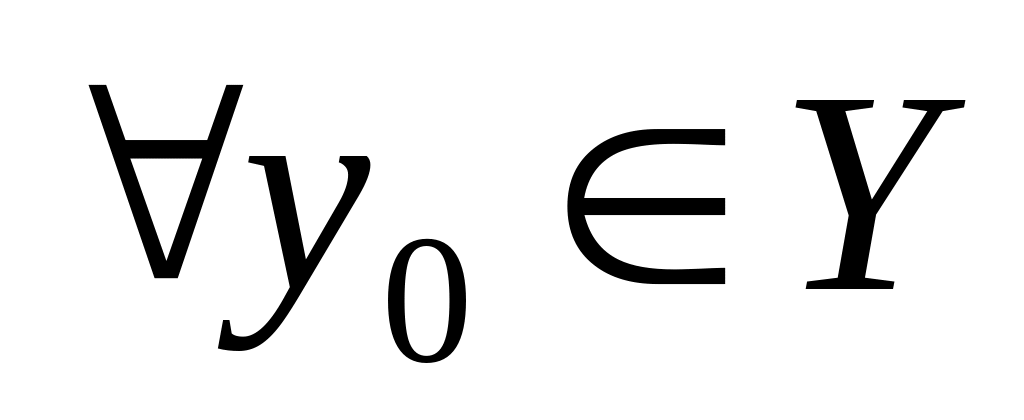 .
Тогда
.
Тогда
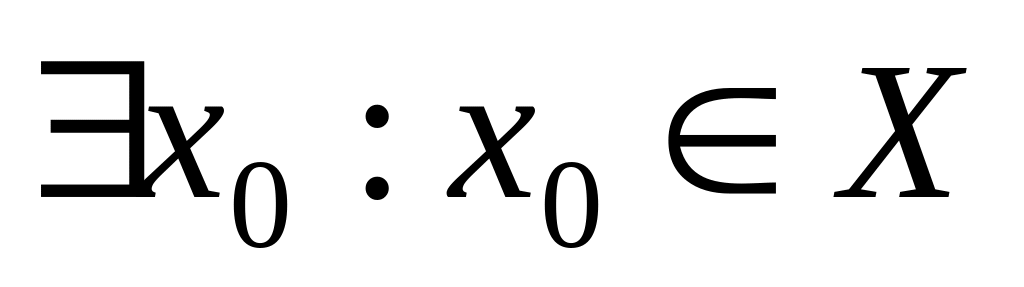 и
и
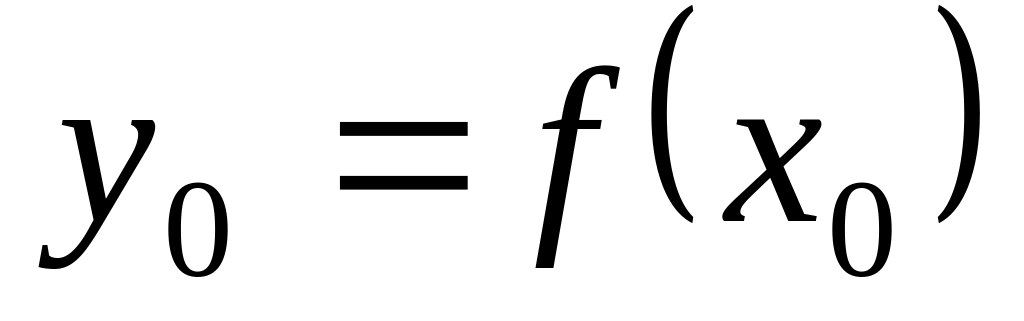 .
Такое
единственно, т.к. если взять
.
Такое
единственно, т.к. если взять  ,
то будет
,
то будет
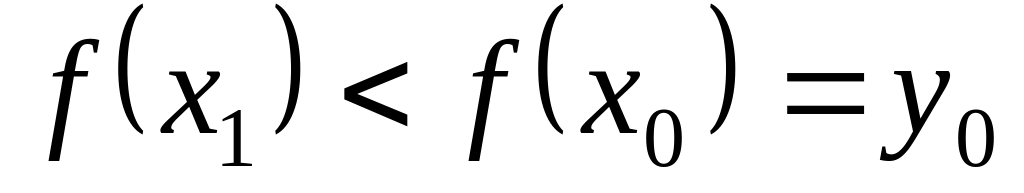 ,
а если взять
,
а если взять
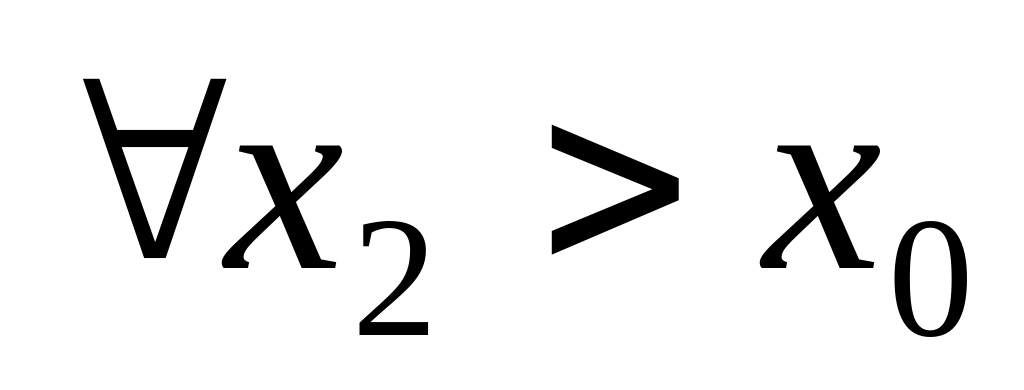 ,
то будет
,
то будет
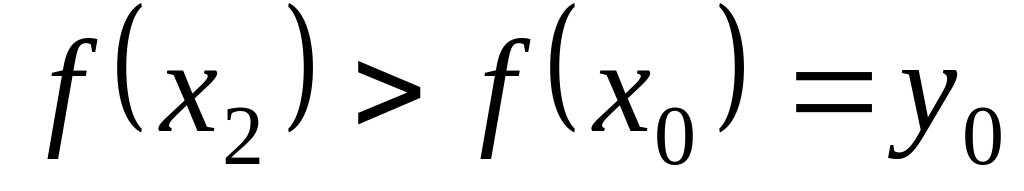 .
Поставив в соответствие всем
.
Поставив в соответствие всем
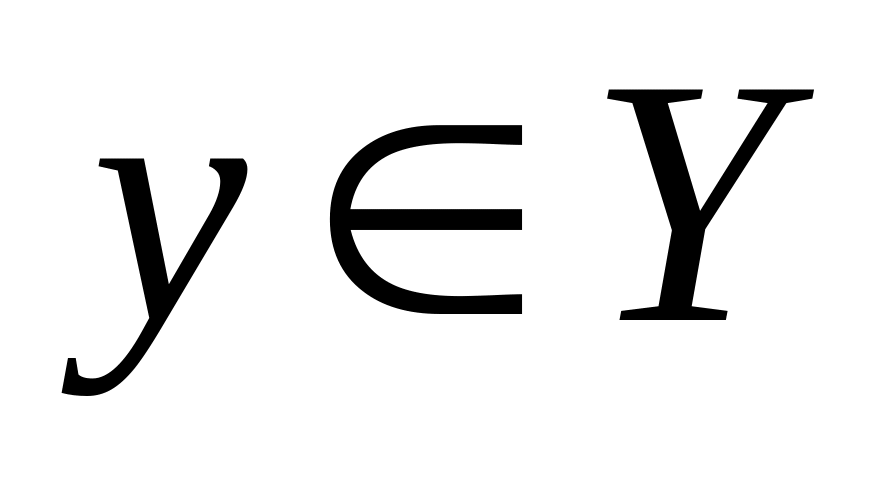 такое x (единственное),
что
такое x (единственное),
что
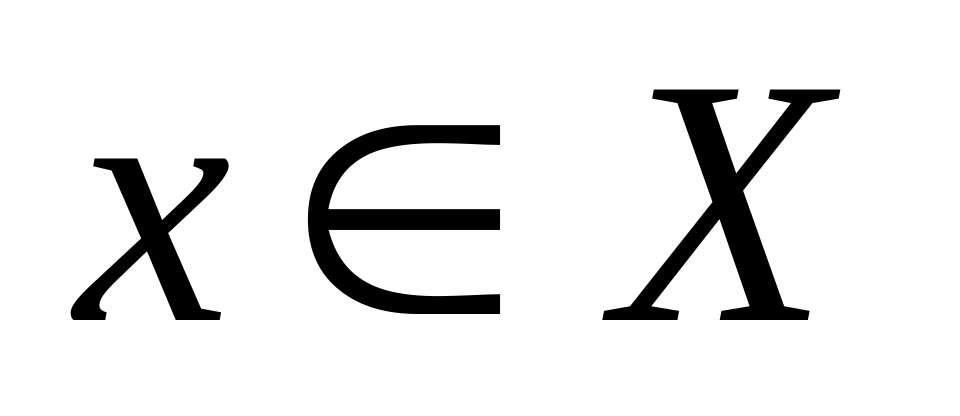 и
и
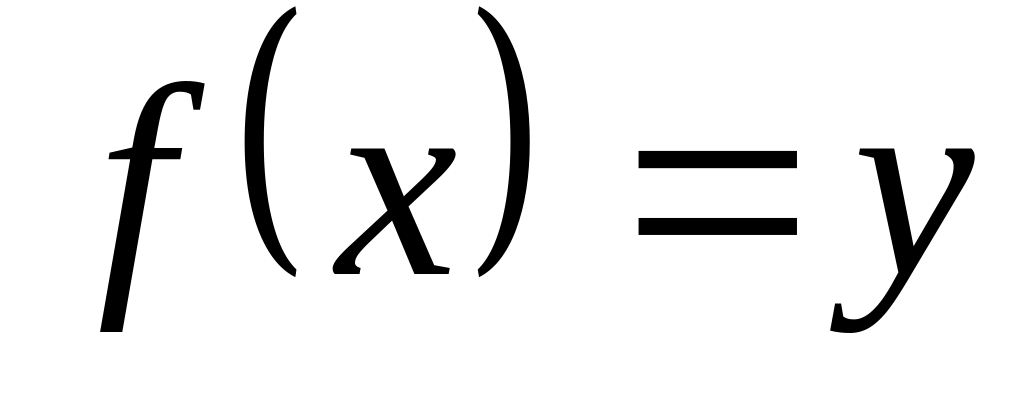 ,
мы получим функцию
,
мы получим функцию
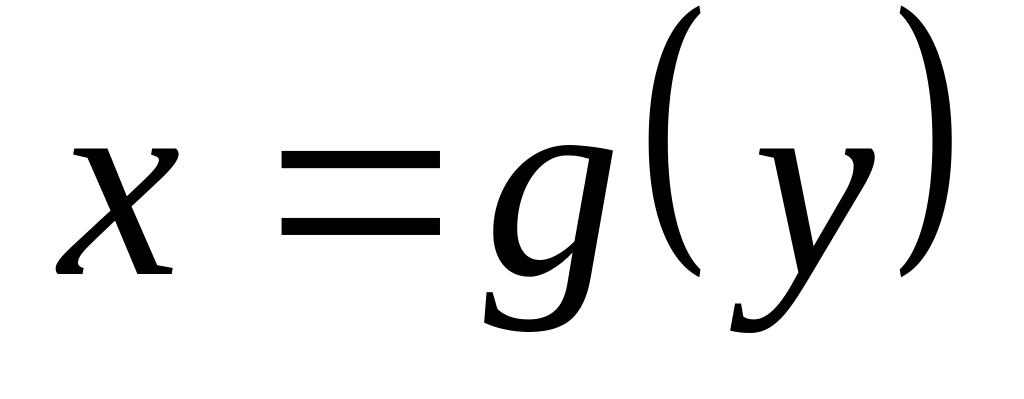 ,
обратную
.
,
обратную
.Теперь докажем монотонность (возрастание). Возьмём
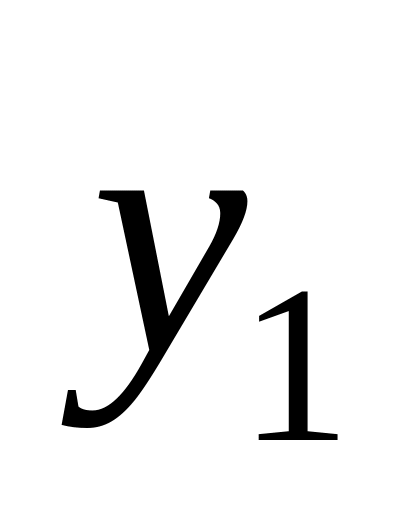 и
и
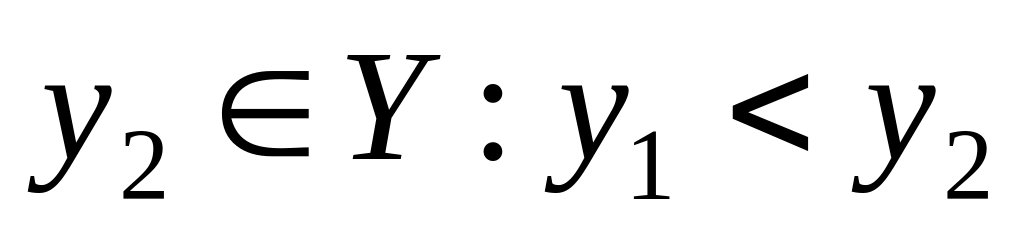 и пусть
и пусть
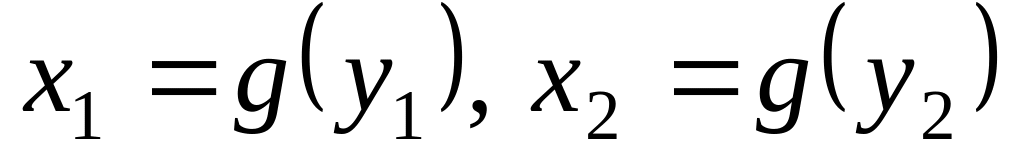 .
Тогда обязательно будет
.
Действительно, если бы было
.
Тогда обязательно будет
.
Действительно, если бы было
 ,
то из-за того, что
,
то из-за того, что
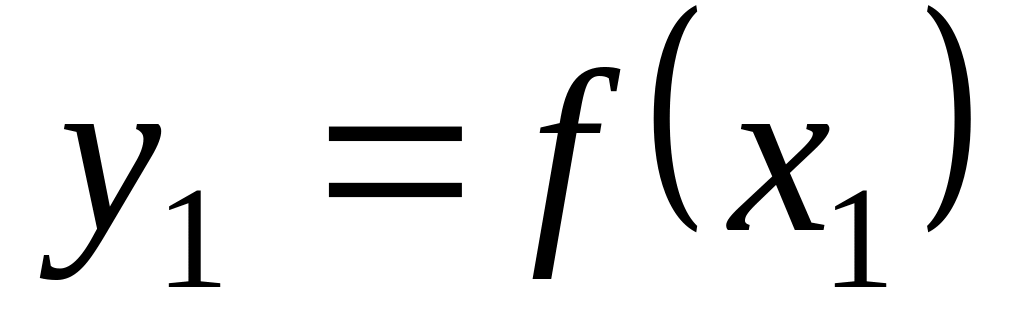 ,
,
 и
и
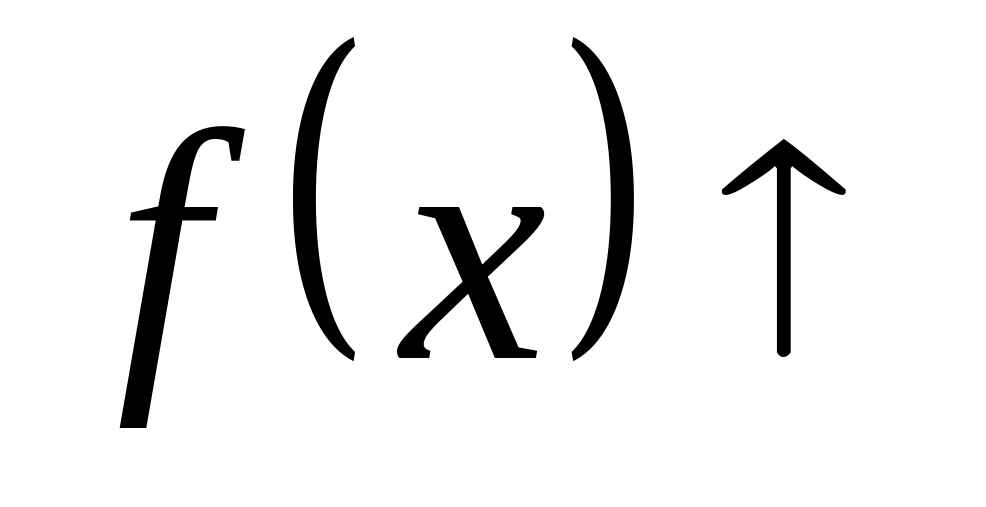 ,
было бы
,
было бы
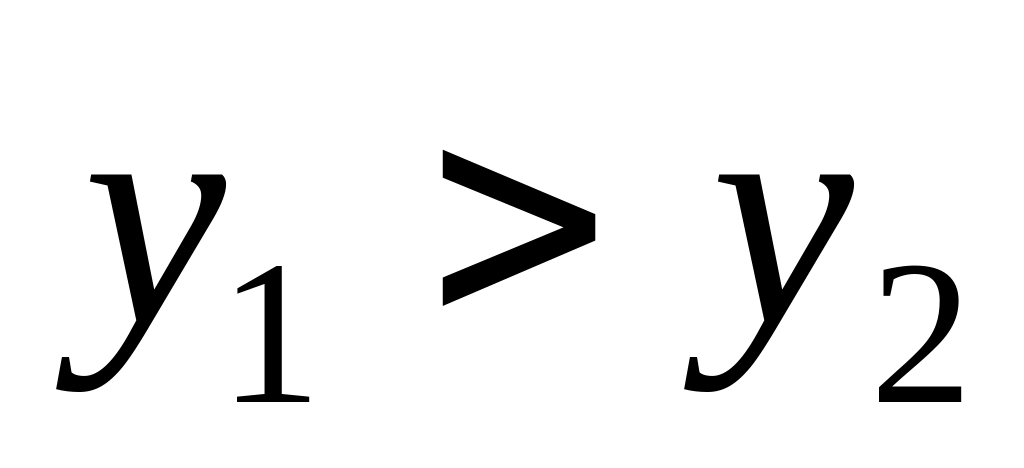 ,
что противоречит условию. Не может быть
и
,
что противоречит условию. Не может быть
и
 ,
т.к. тогда бы
,
т.к. тогда бы
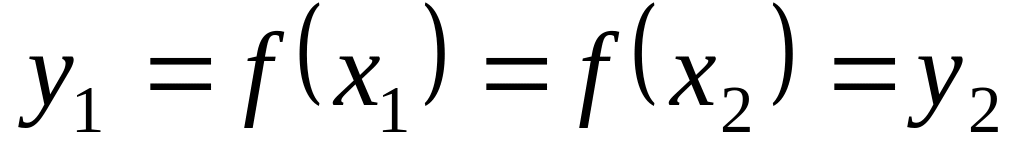 ,
что тоже противоречит условию. Итак,
,
что тоже противоречит условию. Итак,
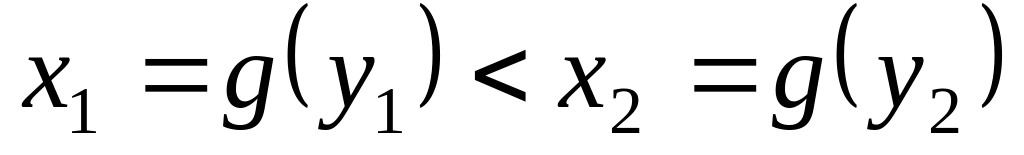 ,
т.е.
возрастает.
,
т.е.
возрастает.Наконец, непрерывность следует из того, что монотонна; её значения сплошь заполняют промежуток X.
I теорема Вейерштрасса: Пусть непрерывна на отрезке . Тогда ограничена на .
Предположим, что
не ограничена на
,
т.е. для
![]() .
.
![]() ограничена, следовательно,
ограничена, следовательно,
![]() и
и
![]() .
Тогда
.
Тогда
![]() и, значит, в точке
и, значит, в точке
![]() непрерывна. Следовательно,
непрерывна. Следовательно,
![]() .
С другой стороны,
при
и, значит, при
.
С другой стороны,
при
и, значит, при
![]() будет
будет
![]() .
Окончательно:
и
.
Окончательно:
и
![]() ,
чего быть не может.
,
чего быть не может.
II теорема Вейерштрасса: Если непрерывна на , то достигает на своих наибольшего наименьшего значений.
Докажем для наибольшего значения. По I
теореме Вейерштрасса у
на
существует конечный
![]() .
Докажем, что
.
Докажем, что
![]() .
По определению
.
По определению
![]() ,
для
найдётся
,
для
найдётся
![]()
![]() .
По лемме Больцано-Вейерштрасса,
.
По лемме Больцано-Вейерштрасса,
![]() и
и
![]() .
Тогда
.
Тогда
![]() .
Следовательно, в точке
непрерывна, а, значит,
.
Следовательно, в точке
непрерывна, а, значит,
![]() .
При
неравенство
.
При
неравенство
![]() переходит в
переходит в
![]() .
Но, т.к.
.
Но, т.к.
![]() ,
то обязательно
,
то обязательно
![]() .
Следовательно,
.
Следовательно,
![]() .
.
