Раскрытие неопределённостей (правила Лоппиталя)

Пусть

1. и определены на некотором промежутке .

2. .

3. в промежутке и дифференцируемы, причём .

4. Существует (конечный или нет) .

Тогда .

Доопределим и в точке : , . Тогда на и будут непрерывны. Тогда в некоторой окрестности точки a, т.к. если бы , то между x и a должна была бы быть точка , что противоречит условию. По теореме Коши , где C – некоторая точка и . Поэтому, если , то будет .

Пусть

1. и определены на ,

2. ,

3. На и дифференцируемы, причём ,

4. .

Тогда

Заменим . Тогда . По условию . Остальные условия тоже выполняются. По предыдущей теореме .

Пусть

1. и определены на ,

2. ,

3. и дифференцируемы на и ,

4. .

Тогда .

Заметим, что . Поэтому можно считать, что на (в крайнем случае, промежуток можно сократить). Рассмотрим случай конечного k. Возьмём . Тогда для будет . Обозначим и возьмём . Тогда , где , следовательно, будет выполняться неравенство . Имеем . Т.к. и точка фиксирована, то для того же при будет , . Но тогда . Это и значит, что .

Пусть теперь . Тогда ( , иначе ). Тогда .

Исследование функций

Пусть непрерывна на и дифференцируема хотя бы на . Для того, чтобы была постоянна на всём необходимо и достаточно, чтобы на .

1. Пусть . Тогда .

2. Пусть на . Возьмём и зафиксируем. Тогда по теореме Лагранжа для будет . Т.к. , то 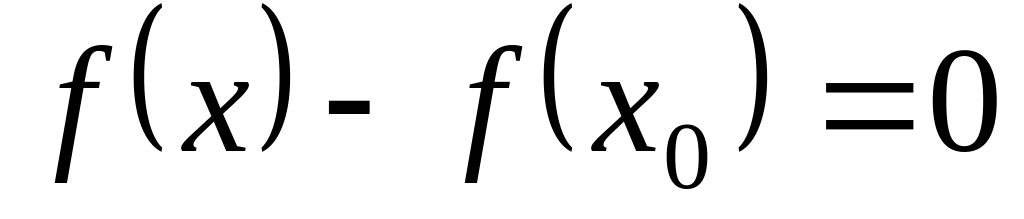, т.к. , т.е. для будет .

Если и – две первообразные для на промежутке X, то .

Имеем .

Пусть непрерывна на и дифференцируема хотя бы на . Для того, чтобы не убывала на , необходимо и достаточно, чтобы было на .

1. Пусть не убывает на . Возьмём и . Тогда при будет , а при будет . И, значит, при и . Тогда .

2. Пусть на . Возьмём и . Тогда по теореме Лагранжа , где . Следовательно, , т.е. не убывает.

Пусть непрерывна на , дифференцируема хотя бы на . Тогда для того, чтобы возрастала на , необходимо и достаточно, чтобы было и ни на каком интервале конечной длины .

1. Пусть строго возрастает на . Тогда по предыдущей теореме и не может на , т.к. тогда на , т.е. функция не являлась бы строго возрастающей.

2. Пусть и ни на каком интервале . Тогда по предыдущей теореме функция не убывает. При этом строго возрастает, т.к. если бы при было бы , то из-за неубывания было бы при на , т.е. при , что противоречит условию.

Необходимое условие локального экстремума: Если точка – точка локального экстремума для , то , либо не существует.

I достаточный признак экстремума: Пусть точка подозрительна на экстремум, в этой точке непрерывна и пусть существует на . Тогда если при переходе через точку меняет знак, то в точке – экстремум. С «–» на «+» – минимум, с «+» на «–» – максимум. Если сохраняет знак, то экстремума нет.

1. Пусть меняет знак при переходе через точку с «+» на «–». Тогда на и на возрастает, т.е. для 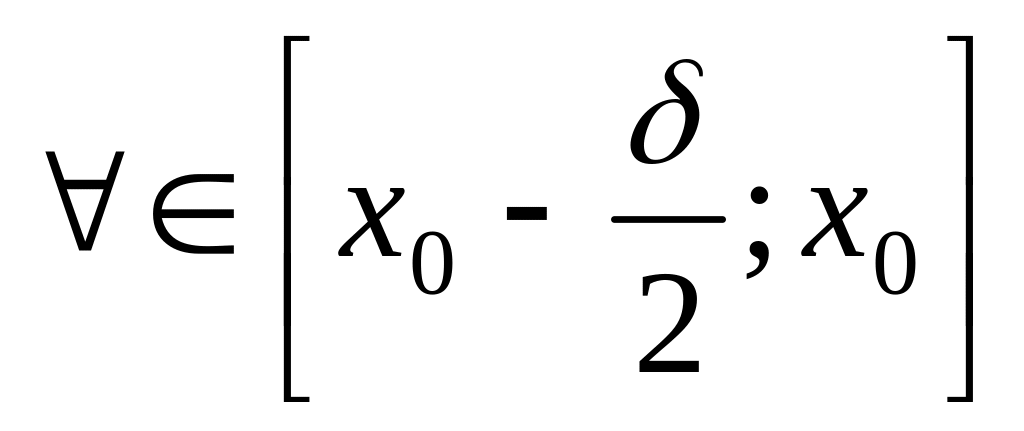будет . Аналогично на убывает, т.к. на для будет ­ , следовательно, в точке – максимум.

2. Пусть не меняет знак. Например, и на , и на . Тогда и на , и на возрастает, т.е. при будет , при будет , следовательно, экстремума нет.

II достаточный признак экстремума: Пусть и существует . Если , то в точке – минимум, а если , то в точке – максимум.

Пусть, например, . Тогда в некоторой окрестности точки существует первая производная и возрастает в точке , т.е. при будет , т.е. , а при будет т.е. , следовательно, при переходе через меняет знак с «–» на «+» и, значит, в точке у минимум.