
- •Последовательности и их пределы
- •Подпоследовательности и частичные пределы
- •Критерий сходимости последовательности.
- •Предел функции и его свойства
- •Классификация бесконечно больших и бесконечно малых функций
- •Равномерная непрерывность функции
- •Раскрытие неопределённостей (правила Лоппиталя)
- •Исследование функций
- •Выпуклость в точке перегиба
Подпоследовательности и частичные пределы
Пусть дана последовательность
и последовательность натуральных чисел
![]() для
для
![]() .
Последовательность
.
Последовательность
![]() называется подпоследовательностью
.
называется подпоследовательностью
.
Если
![]() – последовательность натуральных числе
и
– последовательность натуральных числе
и
![]() ,
то
,
то
![]() .
.
Следует из того, что
![]() (т.к.
каждое слагаемое здесь
(т.к.
каждое слагаемое здесь
![]() )
)![]()
Если
![]() ,
то для любой подпоследовательности
будет
,
то для любой подпоследовательности
будет
![]() .
.
Пусть a конечно. Тогда для
 для
будет
.
Возьмём
для
будет
.
Возьмём
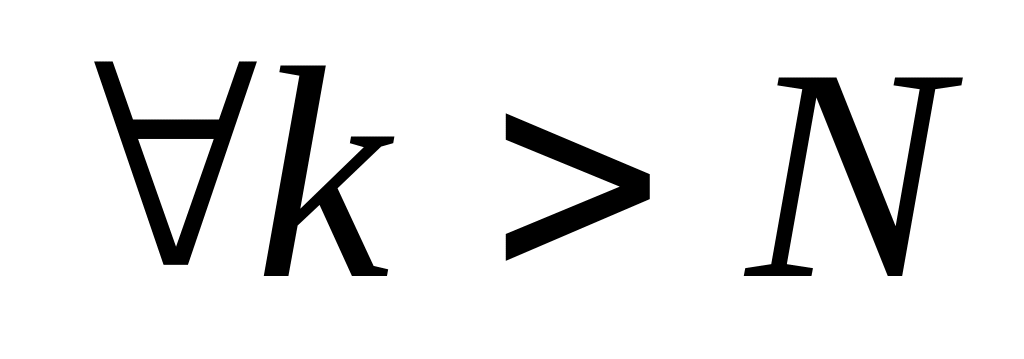 .
Тогда
.
Тогда
 и, следовательно, для
будет
и, следовательно, для
будет
 ,
т.е.
.
,
т.е.
.Пусть
 .
Тогда для
.
Тогда для
 для
будет
для
будет
 .
Отсюда для
будет
.
Отсюда для
будет
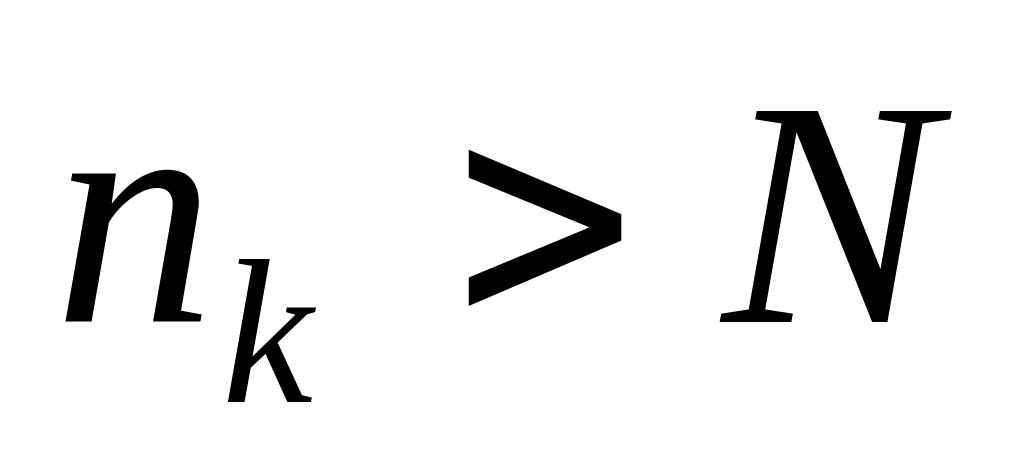 и, значит, при
и, значит, при
 ,
т.е.
,
т.е.
 .
.
Предел подпоследовательности называется частичным пределом.
Лемма Больцано-Вейерштрасса: Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Пусть дана
,
причём
![]() .
Разделим
.
Разделим
![]() пополам точкой
пополам точкой
![]() .
Тогда хотя бы в одном из отрезков
.
Тогда хотя бы в одном из отрезков
![]() лежит бесконечно много элементов
последовательности
.
Тот отрезок, на котором это выполняется,
обозначим
лежит бесконечно много элементов
последовательности
.
Тот отрезок, на котором это выполняется,
обозначим
![]() (если оба – левый). Повторим операцию и
обозначим
(если оба – левый). Повторим операцию и
обозначим
![]() тот отрезок, в котором лежит бесконечно
много элементов
(если оба, то снова левый). Продолжаем
процесс. В результате получим
последовательность вложенных отрезков
тот отрезок, в котором лежит бесконечно
много элементов
(если оба, то снова левый). Продолжаем
процесс. В результате получим
последовательность вложенных отрезков
![]()
![]() ,
причём длина
,
причём длина
![]() ,
и все
содержат бесконечно много
.
По лемме о вложенных отрезках, существует
единственная точка
.
Построим искомую подпоследовательность.
Выберем
,
и все
содержат бесконечно много
.
По лемме о вложенных отрезках, существует
единственная точка
.
Построим искомую подпоследовательность.
Выберем
![]() произвольно из
произвольно из
![]() .
Затем из
выберем
.
Затем из
выберем
![]() .
Это возможно, т.к. в
лежит бесконечно много
.
Аналогично выберем
из
.
Это возможно, т.к. в
лежит бесконечно много
.
Аналогично выберем
из
![]() .
Получим подпоследовательность
.
Получим подпоследовательность
![]() .
Т.к.
.
Т.к.
![]() и
и
![]() ,
то и
,
то и
![]() ,
т.е.
,
т.е.
![]() сходится.
сходится.
Если не ограничена, то она обязательно имеет бесконечный частичный предел.
Пусть, например,
не ограничена сверху. Тогда для
существует бесконечно много элементов
(иначе можно было бы найти наибольший
из них и взять за верхнюю границу).
Построим
следующим образом: берём
![]() .
Потом
.
Потом
![]() и т.д. Тогда очевидно, что
и т.д. Тогда очевидно, что
![]() .
.
Вывод: у всякой последовательности всегда имеются частичные пределы, хотя бы один.
Число a является частичным пределом тогда и только тогда, когда в любой окрестности числа a лежит бесконечно много элементов .
Пусть a – частичный предел последовательности . Тогда
 .
Возьмём
.
Тогда в интервале
.
Возьмём
.
Тогда в интервале
 будут лежать все
,
начиная с некоторого. Следовательно,
в любой окрестности лежит бесконечно
много
.
Если
будут лежать все
,
начиная с некоторого. Следовательно,
в любой окрестности лежит бесконечно
много
.
Если
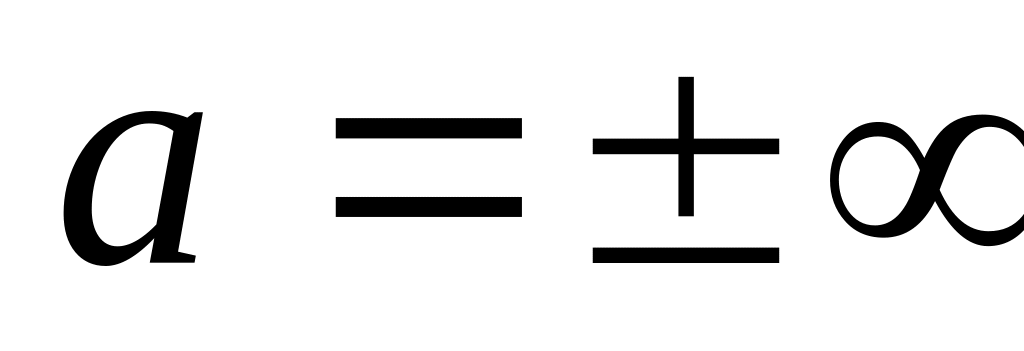 ,
то для
,
то для
 для
для
 в окрестности
в окрестности
 (или
(или
 )
будет лежать бесконечно много
.
)
будет лежать бесконечно много
.Пусть, наоборот, в любой окрестности a лежит бесконечно много членов . Рассмотрим случай конечного a. Возьмём и в окрестности выберем произвольно . Затем в окрестности
 выберем
выберем
 так, что
так, что
 .
Это возможно, т.к. в этой окрестности
бесконечно много
.
Получим подпоследовательность
,
причём
.
Это возможно, т.к. в этой окрестности
бесконечно много
.
Получим подпоследовательность
,
причём
 .
По теореме о зажатой переменной
.
По теореме о зажатой переменной
 ,
т.е. a – частичный
предел.
,
т.е. a – частичный
предел.
То, что число a является пределом последовательности, означает, что в любой окрестности a лежат все члены последовательности, начиная с некоторого, а то, что число a является пределом подпоследовательности, означает, что в любой окрестности a лежит бесконечно много членов последовательности.
Пусть дана
,
и непустое множество A
– множество её частичных пределов.
Тогда
называется верхним
пределом
(обозначается
![]() )
а
)
а
![]() – нижним пределом
(обозначается
– нижним пределом
(обозначается
![]() ).
).
Теорема о принадлежности крайних пределов к частичным: – наибольший, а – наименьший из частичных пределов.
Достаточно доказать, что – частичный (тогда он наибольший).
Пусть, сначала,
 ,
где a – конечное
число. Докажем, что в любой окрестности
a лежит бесконечно
много членов
.
Возьмём
.
По определению
,
где a – конечное
число. Докажем, что в любой окрестности
a лежит бесконечно
много членов
.
Возьмём
.
По определению
 .
Но y – частичный
предел
,
т.к. y принадлежит
множеству частичных пределов A.
Значит, на
.
Но y – частичный
предел
,
т.к. y принадлежит
множеству частичных пределов A.
Значит, на
 будет лежать бесконечно много
.
будет лежать бесконечно много
.
 ,
,
 ,
т.е.
,
т.е.
 и, следовательно, на
при
лежит бесконечно много
и, следовательно, на
при
лежит бесконечно много
 – частичный предел.
– частичный предел.Пусть
 .
Тогда множество частичных пределов A
не ограничено сверху. Отсюда следует,
что
не ограничено сверху (если бы выполнялось
,
то все частичные пределы были бы меньше
M). Значит,
последовательность имеет частичный
предел, равный .
.
Тогда множество частичных пределов A
не ограничено сверху. Отсюда следует,
что
не ограничено сверху (если бы выполнялось
,
то все частичные пределы были бы меньше
M). Значит,
последовательность имеет частичный
предел, равный .
Если
при всех
n,
начиная с некоторого, то
![]() .
Следует из того, что
.
Следует из того, что
![]() и, т.к.
и, т.к.
![]() ,
то и
,
то и
![]() .
Аналогично для
.
.
Аналогично для
.
