
- •Последовательности и их пределы
- •Подпоследовательности и частичные пределы
- •Критерий сходимости последовательности.
- •Предел функции и его свойства
- •Классификация бесконечно больших и бесконечно малых функций
- •Равномерная непрерывность функции
- •Раскрытие неопределённостей (правила Лоппиталя)
- •Исследование функций
- •Выпуклость в точке перегиба
Равномерная непрерывность функции
называется
равномерно непрерывной
на X,
если для
для
и
![]() и удовлетворяющих неравенству
и удовлетворяющих неравенству
![]() будет
будет
![]() .
.
Колебанием функции на
множестве X
называется величина
![]()
Теорема Кантора: Если функция непрерывна на отрезке, то она равномерно непрерывна на нём.
Пусть
не является равномерно непрерывной на
.
Тогда
![]() для
натурального
для
натурального
![]() и
и
![]() и
и
![]() ,
но при этом
,
но при этом
![]() .
По лемме Больцано-Вейерштрасса из
.
По лемме Больцано-Вейерштрасса из
![]() можно выделить сходящуюся
подпоследовательность
можно выделить сходящуюся
подпоследовательность
![]() .
Тогда
.
Тогда
![]() ,
где
,
где
![]() ,
т.е.
,
т.е.
![]() при
при
![]() .
Т.к.
,
то
непрерывна в точке
.
Т.к.
,
то
непрерывна в точке
![]() и, значит,
и, значит,
![]() ,
,
![]() ,
и, поэтому,
,
и, поэтому,
![]() ,
но этого быть не может, т.к.
,
но этого быть не может, т.к.
![]() .
Полученное противоречие показывает
теорему.
.
Полученное противоречие показывает
теорему.
Если
непрерывна на
,
то существует разбиение
![]() такое что
такое что
![]() для
для
![]() .
.
Т.к.
непрерывна на
,
то
равномерно непрерывна на
,
следовательно, для
для
![]() и
и
![]() будет
будет
![]() .
Разобьём отрезок
точками
так, что все
.
Разобьём отрезок
точками
так, что все
![]() .
Рассмотрим теперь
.
Рассмотрим теперь
![]() .
Пусть
.
Пусть
![]() ,
а
,
а
![]() .
Т.к.
.
Т.к.
![]() ,
то
,
то
![]() для
.
для
.
Если равномерно непрерывна на множестве X, то непрерывна на множестве X.
То, что
равномерно непрерывна, означает, что
для
для
и
![]() будет
,
т.е.
будет
,
т.е.
![]() для
для
![]() ,
что полностью подходит под определение
непрерывной на отрезке функции.
,
что полностью подходит под определение
непрерывной на отрезке функции.
Непрерывность элементарных функций
 – непрерывна везде, т.к.
– непрерывна везде, т.к.
 .
.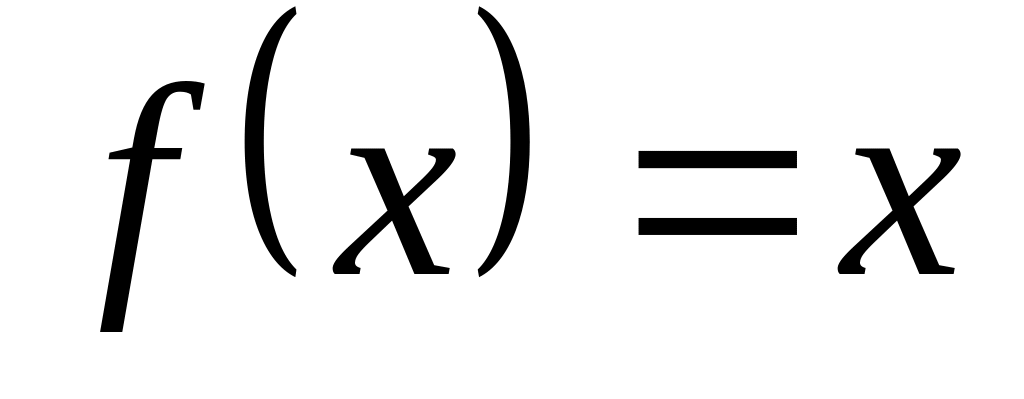 – непрерывна везде, т.к. если взять
– непрерывна везде, т.к. если взять
 ,
то из
,
то из
 следует
следует
 .
. (n – натуральное) –
непрерывна везде как произведение
непрерывных функций.
(n – натуральное) –
непрерывна везде как произведение
непрерывных функций.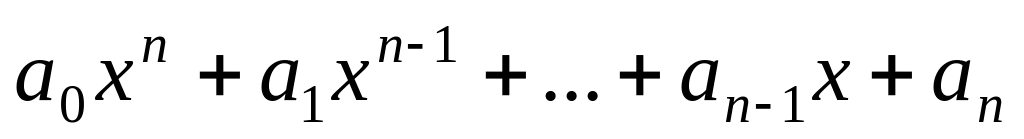 – непрерывна везде как сумма непрерывных
функций.
– непрерывна везде как сумма непрерывных
функций. – непрерывна везде, кроме тех x,
при которых знаменатель равен нулю.
– непрерывна везде, кроме тех x,
при которых знаменатель равен нулю. .
Пусть
.
Пусть
 .
Тогда
.
Тогда
 .
Для функции
.
Для функции
 известно, что она непрерывна на
известно, что она непрерывна на
 .
Кроме того, если
.
Кроме того, если
 ,
то
,
то
 возрастает. Следовательно,
определена на
,
строго возрастает и непрерывна.
возрастает. Следовательно,
определена на
,
строго возрастает и непрерывна. .
Рассмотрим
.
Рассмотрим

 ,
т.е.
,
т.е.
 .
Возьмём
и положим
.
Тогда, если
.
Возьмём
и положим
.
Тогда, если
 ,
то
,
то
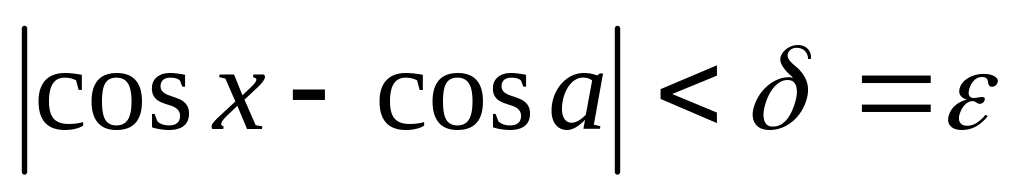 ,
следовательно,
,
следовательно,
 ,
а так как это верно для любого a,
то
непрерывна везде.
,
а так как это верно для любого a,
то
непрерывна везде. – непрерывна везде.
– непрерывна везде. – непрерывна везде, кроме
– непрерывна везде, кроме
 .
. – непрерывна везде, кроме
– непрерывна везде, кроме
 .
. – непрерывны на
– непрерывны на
 по определению.
по определению. – непрерывны везде по определению.
– непрерывны везде по определению.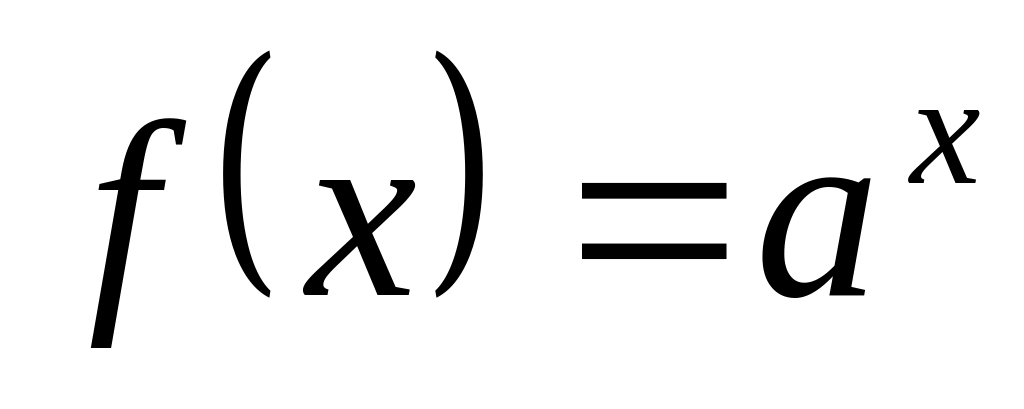 .
.
а) Докажем, что ![]() .
Имеем
.
Имеем
![]() для
для
![]() .
.
б) Докажем, что
![]() .
Заметим, что
.
Заметим, что
![]() при
,
а
при
,
а
 при
.
Возьмём
.
Тогда
при
будет
при
.
Возьмём
.
Тогда
при
будет
![]() .
Зафиксируем
.
Зафиксируем
![]() .
Тогда
.
Тогда
![]() .
Т.к.
,
то, взяв
.
Т.к.
,
то, взяв
![]() ,
будем иметь для
,
будем иметь для
![]()
![]() .
Тогда
.
Тогда
![]() ,
т.е.
,
т.е.
![]() при
,
откуда
.
при
,
откуда
.
в )
Докажем, что
)
Докажем, что
![]() .
Имеем
.
Имеем
![]() ,
т.е.
непрерывна при
,
т.е.
непрерывна при
![]() ,
а т.к.
– любое, то
непрерывна везде.
,
а т.к.
– любое, то
непрерывна везде.
г) Монотонность (при
![]() ).
Пусть
.
Тогда
).
Пусть
.
Тогда
![]() .
Т.к.
.
Т.к.
![]() ,
то
,
то
![]() ,
следовательно,
,
следовательно,
![]() ,
т.е. функция монотонно возрастает.
,
т.е. функция монотонно возрастает.
 – непрерывна на
– непрерывна на
 из теоремы об обратной функции.
из теоремы об обратной функции.
Доказательство некоторых эквивалентностей:
 .
.
 .
. .
.
 .
. .
.
 .
.
Дифференциальное исчисление
Производная
в точке x
![]() .
.
![]() – правосторонняя
производная в точке x.
– правосторонняя
производная в точке x.
Некоторые производные:

 .
. .
. .
. .
. .
. .
. .
.
Приращение дифференциальной функции:
Если
дифференцируема в точке
(т.е. имеет конечную производную), то
![]()
![]() ,
где
,
где
![]() при
при
![]() .
Равенство сохраняется и при
.
Равенство сохраняется и при
![]() .
При этом будем полагать
.
При этом будем полагать
![]() .
.
Имеем
![]() при
.
Обозначим
при
.
Обозначим
![]() .
Тогда
.
Тогда
![]() ,
где
,
где
![]() .
.
Если дифференцируема в точке , то непрерывна в точке .
Т.к.
![]() ,
то при
,
то при
![]() функция
непрерывна.
функция
непрерывна.
Правила дифференцирования:
![]() .
.
Если
и
![]() дифференцируемы в точке
,
то в точке
существуют
дифференцируемы в точке
,
то в точке
существуют
 .
. ,
где
,
где
 .
. .
. .
.
Пусть
 .
Тогда
.
Тогда
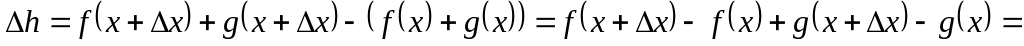
 .
Отсюда
.
Отсюда
 .
.Пусть
 .
Тогда
.
Тогда
 ,
откуда
,
откуда

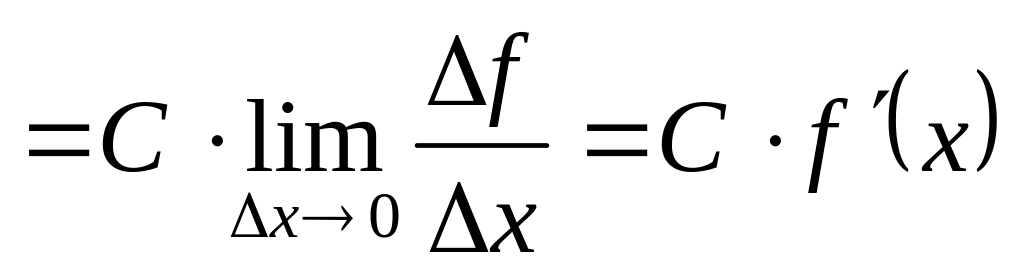 .
.Пусть
 .
Тогда
.
Тогда
 ,
откуда
,
откуда
 (т.к.
(т.к.
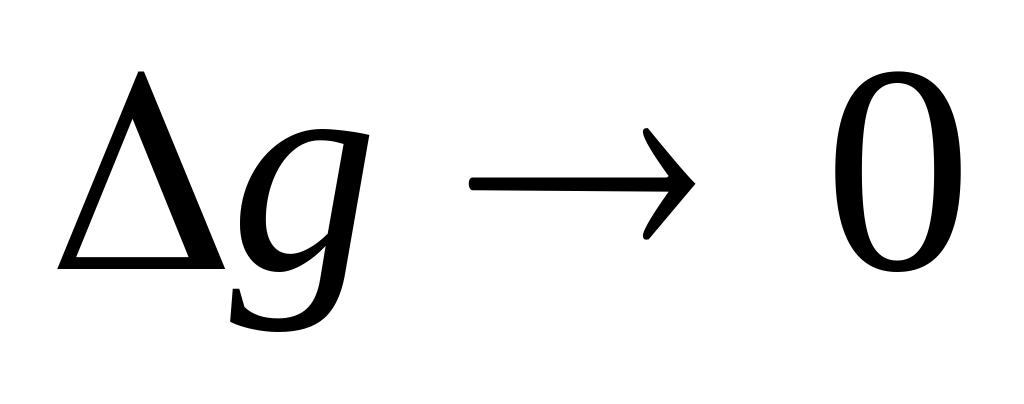 при
(следует из непрерывности
)).
при
(следует из непрерывности
)).Пусть
 .
Тогда
.
Тогда
 ,
откуда
,
откуда
 (т.к.
при
(следует из непрерывности
)).
(т.к.
при
(следует из непрерывности
)).
Пусть
дифференцируема в точке
и определена в некоторой окрестности
точки
,
функция
![]() дифференцируема в соответствующей
точке
и значения
,
когда x
принадлежит некоторой окрестности
точки
,
попадают в некоторую окрестность точки
дифференцируема в соответствующей
точке
и значения
,
когда x
принадлежит некоторой окрестности
точки
,
попадают в некоторую окрестность точки
![]() .
Тогда сложная функция
.
Тогда сложная функция
![]() будет дифференцируема в точке
,
причём
будет дифференцируема в точке
,
причём
![]() .
.
Придадим x приращение
![]() .
Тогда
получит приращение
.
Тогда
получит приращение
![]() .
Аналогично,
.
Аналогично,
![]() получит приращение
получит приращение
![]() .
По формуле приращения будет
.
По формуле приращения будет
![]() ,
где
,
где
![]() при
при ![]() .
Отсюда
.
Отсюда
![]() .
.
![]()
![]() (т.к.
и
).
(т.к.
и
).
Теорема о производной обратной функции:
Пусть
в некоторой окрестности точки
строго возрастает или строго убывает
и непрерывна и пусть существует
![]() .
Тогда в некоторой окрестности
соответствующей точки
определена обратная функция
,
причём существует
.
Тогда в некоторой окрестности
соответствующей точки
определена обратная функция
,
причём существует
![]() .
.
По теореме о непрерывности обратной
функции в некоторой окрестности точки
существует обратная функция
,
строго монотонная и непрерывная. Придадим
y приращение
.
Тогда
![]() .
Причём при
будет
.
Отсюда
.
Причём при
будет
.
Отсюда
![]()
 .
.
Пример:
 .
. .
.
Дифференциал функции
Если
дифференцируема в точке
,
то
![]() ,
следовательно, при
выражение
,
следовательно, при
выражение
![]() – главная часть приращения
– главная часть приращения
![]() .
.
Е сли
дифференцируема в точке
,
то выражение
сли
дифференцируема в точке
,
то выражение
![]() называется дифференциалом
в точке
.
При этом для симметрии записывают
как
называется дифференциалом
в точке
.
При этом для симметрии записывают
как
![]() .
Тогда
.
Тогда ![]() .
.
Теорема об инвариантности формы
первого дифференциала: Дифференциал
дифференцируемой функции
![]() может быть написан в виде
может быть написан в виде
![]() как в случае, когда x
– независимая переменная, так и в случае,
когда
как в случае, когда x
– независимая переменная, так и в случае,
когда
![]() – дифференцируемая функция другой
переменной.
– дифференцируемая функция другой
переменной.
Пусть x – независимая переменная. Тогда
 по определению.
по определению.Пусть
 .
Тогда
.
Тогда
 .
.
Производные и дифференциалы старших порядков
Если на промежутке существует
![]() ,
то
,
то
![]() ,
если она существует.
,
если она существует.
Аналогично
![]() .
.
Очевидно, что
![]() ,
,
![]() ,
где
,
где
![]() .
.
Некоторые формулы:
 ,
,
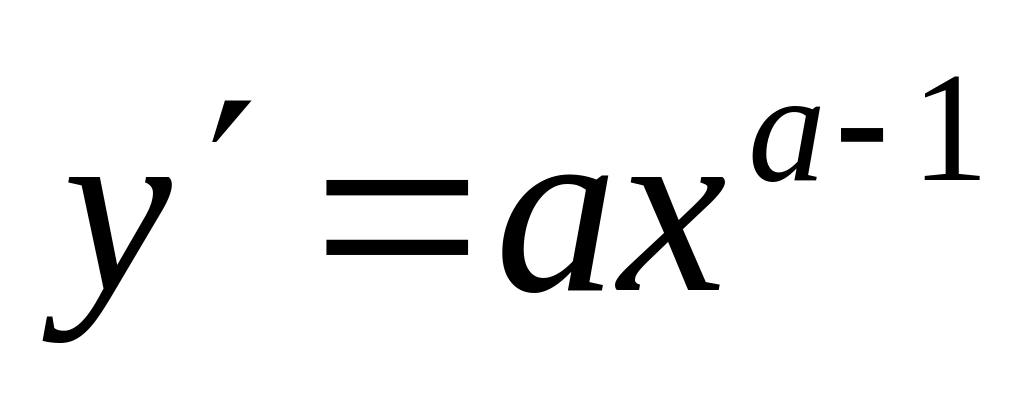 ,
,
 ,
…,
,
…,
 .
Если a – натуральное,
то
.
Если a – натуральное,
то
 при
при
 и
и
 при
при
 .
. ,
,
 .
. ,
,
 .
. ,
,
 .
. ,
,
 .
. ,
,
 ,
,
 ,
,
 ,
,
 .
.
 ,
,
 .
.Аналогично
 .
.
Формула Лейбница:
![]() .
.
Функция называется n раз дифференцируемой, если у неё существует производная n-го порядка.
n-й
дифференциал
![]() ,
причём приращение x
всё время берётся одно и то же.
,
причём приращение x
всё время берётся одно и то же.
Если x – независимая переменная, то:

Форма дифференциала n-го порядка при переходе от независимой переменной к зависимой не сохраняется.
Пусть
.
Тогда![]() .
.
Параметрическое дифференцирование:
![]() ,
,
![]() ,
,
 ,
,
 .
.
Теоремы о дифференцируемых функциях
Говорят, что
возрастает
в точке
,
если существует такое
![]() ,
что при
,
что при
![]() будет
будет
![]() ,
а при
,
а при
![]() будет
будет
![]() .
.
Пусть
определена в некоторой окрестности
точки
и существует
![]() .
Тогда в точке
возрастает.
.
Тогда в точке
возрастает.
Имеем
![]() .
Тогда
при
.
Тогда
при
![]() будет
будет
![]() .
Отсюда для
.
Отсюда для
![]() будет
будет
![]() ,
т.е.
,
а для
,
т.е.
,
а для
![]() будет
будет
![]() ,
т.е.
,
т.е.
![]() на
на
![]() .
.
Точка
называется точкой
локального максимума для
,
если
в окрестности
будет
![]() (
определена на
).
(
определена на
).
Точки локального максимума и минимума называются точками локального экстремума.
Теорема Ферма: Если
определена на каком-то промежутке, во
внутренней точке
![]() достигает локального экстремума и
существует
достигает локального экстремума и
существует
![]() ,
то
,
то
![]() .
.
Пусть, например,
– точка локального максимума. Тогда не
может быть
,
т.к. тогда бы при
![]() было бы
было бы
![]() ,
что противоречит условию, и не может
быть
,
что противоречит условию, и не может
быть
![]() ,
т.к. тогда бы при
,
т.к. тогда бы при
![]() было бы
,
что противоречит условию, следовательно,
.
было бы
,
что противоречит условию, следовательно,
.
Теорема Ролля: Пусть
непрерывна на ,
дифференцируема хотя бы на
 .
. .
.
Тогда
![]() .
.
Т.к.
непрерывна на
,
то по I теореме Вейерштрасса,
![]() и
,
в которых
достигает своего наибольшего и наименьшего
значений. Возможны два случая:
и
,
в которых
достигает своего наибольшего и наименьшего
значений. Возможны два случая:
 .
Тогда
.
Тогда
 и
и
 для
для
 .
Т.е. за C можно взять
.
.
Т.е. за C можно взять
. .
Т.к.
,
то хотя бы одно их этих значений будет
достигаться во внутренней точке нашего
интервала, т.е. в C
будет локальный экстремум, а т.к.
.
Т.к.
,
то хотя бы одно их этих значений будет
достигаться во внутренней точке нашего
интервала, т.е. в C
будет локальный экстремум, а т.к.
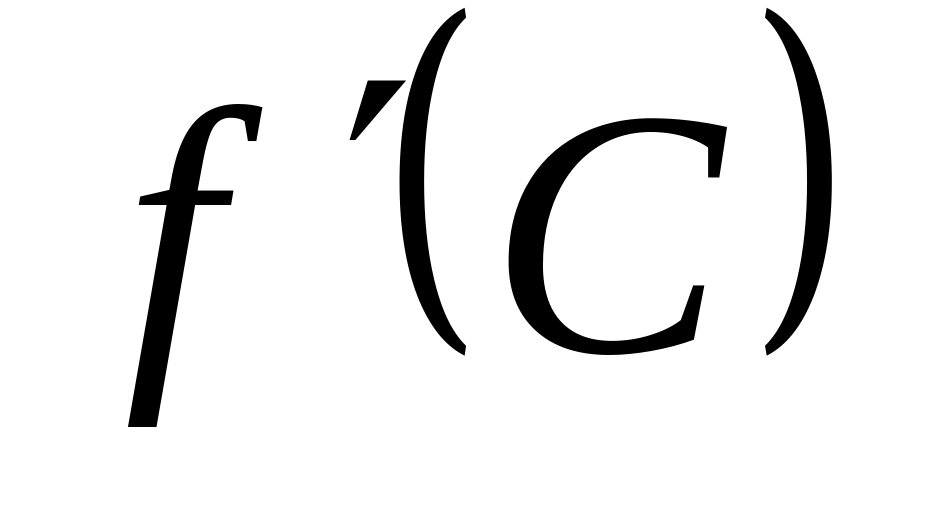 существует, то по теореме Ферма
существует, то по теореме Ферма
 .
.
Теорема Лагранжа: Пусть
непрерывна на ,
дифференцируема хотя бы на .
Тогда
![]() .
.
В ведём
вспомогательную функцию
ведём
вспомогательную функцию
![]() .
Проверим условия теоремы Ролля:
.
Проверим условия теоремы Ролля:
непрерывна на , т.к. является линейной комбинацией непрерывных функций
Дифференцируема на по той же причине, причём
 .
. ,
,
 ,
т.е.
,
т.е.
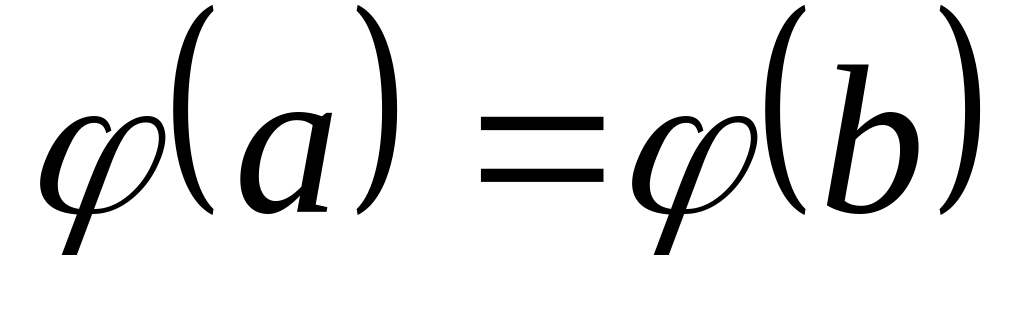 .
.
Т.к.
удовлетворяет условиям теоремы Ролля,
то
![]() ,
т.е.
,
т.е.
![]() или
или
![]() .
.
Теорема Лагранжа верна как
при
,
так и при
![]() .
Часто берут
.
Часто берут
![]() ,
тогда
,
тогда
![]() .
Получаем
.
Получаем
![]() .
Тогда можно обозначить
.
Тогда можно обозначить
![]() ,
,
![]() .
Тогда теорема Лагранжа формулируется
так: Существует
.
Тогда теорема Лагранжа формулируется
так: Существует
![]() ,
что
,
что
![]() .
При этом последнюю формулу называют
формулой конечных
приращений. Есть ещё
одна запись этой теоремы:
.
При этом последнюю формулу называют
формулой конечных
приращений. Есть ещё
одна запись этой теоремы:
![]() .
.
Теорема Коши для дифференцируемых функций: Пусть
и непрерывны на ,
и дифференцируемы хотя бы на ,
 на
.
на
.
Тогда
![]() .
.
Убедимся, что
![]() .
Если бы это было не так, то выполнялись
бы все условия теоремы Ролля, и существовала
бы точка
.
Если бы это было не так, то выполнялись
бы все условия теоремы Ролля, и существовала
бы точка
![]() ,
что противоречит третьему условию.
Введём вспомогательную функцию
,
что противоречит третьему условию.
Введём вспомогательную функцию
![]() .
.
непрерывна на как линейная комбинация непрерывных функций.
дифференцируема на по той же причине, причём
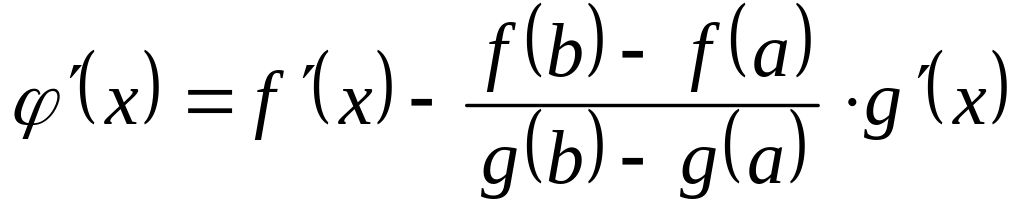 .
.,
 ,
т.е.
.
,
т.е.
.
Значит, по теореме Ролля
,
т.е.
![]() или
или
![]() .
.
Формула Тейлора: Пусть
в некоторой окрестности точки
существует
,
![]() ,
…,
,
…,
![]() и
и
![]() .
Тогда
.
Тогда
![]() .
.
Обозначим
![]() (многочлен Тейлора). При
этом
(многочлен Тейлора). При
этом
![]() ,
,
![]() ,
…,
,
…,
![]() .
Поэтому, если положить
.
Поэтому, если положить
![]() ,
то для
,
то для
![]() будет
будет
![]() ,
,
![]() ,
…,
,
…,
![]() .
Докажем, что
.
Докажем, что
![]() .
.
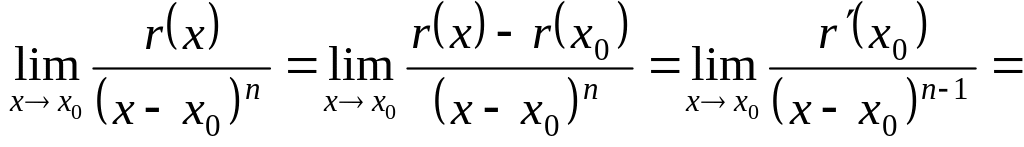
 .
Следовательно,
.
Следовательно,
![]()
![]() .
.
Единственность формулы Тейлора:
Если
![]() и
и
![]() ,
то
,
то
![]() ,
,
![]() ,
…,
,
…,
![]() .
.
Из
![]() следует, что
следует, что
![]() .
Устремим x к
.
Тогда
.
Вычтем
.
Устремим x к
.
Тогда
.
Вычтем
![]() и
и
![]() и поделим на
и поделим на
![]() .
Тогда
.
Тогда
![]() .
Опять устремим x к
.
Получим
.
Аналогично
.
Опять устремим x к
.
Получим
.
Аналогично
![]() ,
,
![]() ,
…,
,
…,
![]() .
.
Если
![]() раз дифференцируема в некоторой
окрестности точки
,
существует
раз дифференцируема в некоторой
окрестности точки
,
существует
![]() и
,
то
и
,
то
![]() ,
где
,
где
![]() .
.
Положим
![]() .
Тогда в условии теоремы
.
Тогда в условии теоремы
![]()
![]() .
.
Пусть на
![]() существуют и непрерывны
,
,
…,
существуют и непрерывны
,
,
…,
![]() ,
а в
,
а в
![]() существует
существует
![]() .
Тогда для
.
Тогда для
![]() существует число
существует число
![]()
![]() для
для
![]() .
.
Нам надо оценить
![]() .
Введём вспомогательную функцию
.
Введём вспомогательную функцию
![]() ,
где z – переменная, а
,
где z – переменная, а
![]() .
.
 непрерывна на
.
непрерывна на
.
 .
Т.к.
.
Т.к.
 существует в
,
то и
существует в
,
то и
 существует в том же интервале.
существует в том же интервале. ,
,
 .
.
Возьмём произвольную функцию
![]() с условиями:
непрерывна, дифференцируема и не равна
нулю на
,
и применим теорему Коши. Получим, что
существует точка
с условиями:
непрерывна, дифференцируема и не равна
нулю на
,
и применим теорему Коши. Получим, что
существует точка
![]() ,
откуда
,
откуда
![]() .
Тогда
.
Тогда
![]()
![]() .
Возьмём
.
Возьмём
![]() ,
тогда
,
тогда
![]() существует на
существует на
![]() и
и
![]() на
.
Отсюда
на
.
Отсюда
![]() .
Т.к.
.
Т.к.
![]() ,
то
,
то
![]() (
).
Тогда
(
).
Тогда
![]() ,
,
![]() .
.
Частные случаи:
Член
![]() называется остаточным
членом в форме Пеано.
называется остаточным
членом в форме Пеано.
При
![]()
![]() называется остаточным
членом в форме Лагранжа.
называется остаточным
членом в форме Лагранжа.
При
![]()
![]() – остаточный член в
форме Коши.
– остаточный член в
форме Коши.
Стандартные разложения:
 .
. .
. .
. .
.
Формула бинома Ньютона:
 .
.
Ряды
Рядом
называется сумма бесконечного числа
слагаемых.
![]() .
.
Сумма
![]() называется частичной
суммой ряда.
называется частичной
суммой ряда.
Если существует конечный
предел
![]() ,
то S
называется суммой ряда.
Говорят, что ряд
сходится
к S.
Если
,
то S
называется суммой ряда.
Говорят, что ряд
сходится
к S.
Если
![]() ,
то говорят, что ряд
расходится
к
,
то говорят, что ряд
расходится
к
![]() .
.
Критерий сходимости ряда: Для
сходимости ряда
![]() необходимо и достаточно, чтобы для
для
и любого натурального p
было бы
необходимо и достаточно, чтобы для
для
и любого натурального p
было бы
![]() .
.
Необходимый признак сходимости ряда:
Если
сходится, то
![]() при
.
при
.
Пусть
сходится и
![]() ,
т.е.
,
т.е.
![]() при
.
Тогда
при
.
Тогда
![]() ,
а значит
,
а значит
![]() .
.
Ряд
называют абсолютно
сходящимся, если сходится
ряд
![]() .
.
Если ряд абсолютно сходится, то он сходится.
Пусть
абсолютно сходится, т.е. сходится
.
Возьмём
.
Тогда по критерию сходимости
для
и
натурального будет
![]() .
Но тогда для того же
и того же N для
и любого натурального p
будет
.
Но тогда для того же
и того же N для
и любого натурального p
будет
![]() .
Тогда по критерию Коши
сходится.
.
Тогда по критерию Коши
сходится.
Ряды вида
![]() называют степенными.
называют степенными.
Степенной ряд
называется рядом Тейлора
для
,
если
![]() .
.
