Дифференцирование функций нескольких переменных

Пусть на множестве A пространства задана функция и пусть – внутренняя точка для A. Тогда . Предел , если он существует, называется частной производной по в точке . Обозначение: или .

Пусть – внутренняя точка для множества A, на котором определена функция . Функция называется дифференцируемой в точке , если для любых достаточно малых существуют числа и бесконечно малые при и .

Если дифференцируема в точке , то называется дифференциалом в точке .

1. Если дифференцируема в точке , то непрерывна в точке .

Т.к. при будет – определение непрерывности на языке приращения.

2. Если дифференцируема в точке , то существуют , причём .

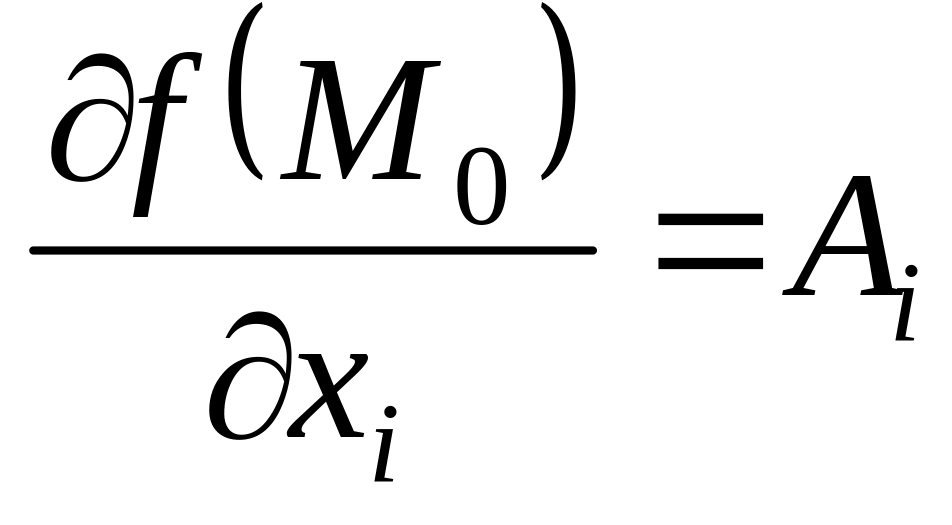Имеем при , т.е. .

3. Единственность дифференциала: , где для независимой переменной.

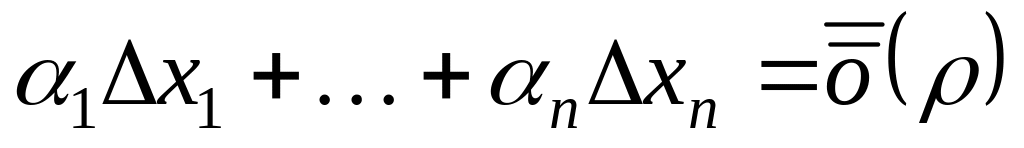4. , где в евклидовом пространстве, т.е. .

а) при , т.е. при .

б) , где при , т.е. при .

Достаточное условие дифференцируемости: Если в некоторой окрестности точки существуют все и все они непрерывны в точке , то дифференцируема в точке .

Д ля простоты пусть , т.е. . Имеем: . Т.к. , то по теореме Лагранжа . Аналогично, . Т.к. и непрерывны в точке , то , где и при . Отсюда , где и при , что и означает дифференцируемость в точке .

Теорема о дифференцируемости сложной функции: Пусть даны функции , причём все дифференцируемы в точке , а дифференцируема в точке , где . Тогда сложная функция дифференцируема в точке , причём частные производные считаются по формуле , где все берутся в точке M, а все берутся в точке T.

Придадим переменным приращение . Тогда получат приращение , а получит приращение f. Т.к. все функции дифференцируемы, то , где при . , где  – расстояние от до T. Отсюда видно, что , где . Поэтому при , т.к. при этом по непрерывности функций в точке T, т.е. . Так же и . Имеем: , откуда и следует утверждение теоремы.

Инвариантность формы первого дифференциала: Дифференциал дифференцируемой функции может быть задан в виде как в случае, когда – независимая переменная, так и когда они сами дифференцируемые функции: .

Например, для и . Отсюда следует сохранение формул дифференцирования, например, . Аналогично .

Производные и дифференциалы высших порядков

Теорема о равенстве смешанных производных: Пусть в некоторой окрестности точки у функции и , причём обе эти функции непрерывны в точке . Тогда .

Пусть у функции существует в некоторой окрестности точки все частные производные до k-го порядка включительно, причём все они непрерывны в точке . Тогда все смешанные производные до k-го порядка включительно не зависят от порядка дифференцирования.

Определение:

Пусть , причём все функции имеют все частные производные до m-го порядка включительно в точке и непрерывны в точке T, а функция имеет все частные производные до m-го порядка и они непрерывны в соответствующей точке , где . Тогда у сложной функции в точке T существуют все частные производные до m-го порядка и все они непрерывны в точке T.

Пусть и – независимые переменные. Тогда , (если смешанные производные равны) (символически) . Аналогично, , если все смешанные производные не зависят от порядка дифференцирования.

Дифференцирование сложных функций

Если , то дифференциалы старших порядков сохраняют форму.

Формула Тейлора

Пусть в некоторой окрестности точки функция и все её частные производные до m+1-го порядка включительно существуют и непрерывны. Тогда для из окрестности точки и .

Обозначим . Введём функции . Тогда , где и . По теореме о сложной функции, будет иметь непрерывные производные вплоть до m+1-го порядка на . Применим к формулу Тейлора: , где . Здесь , (т.к. и ) . Т.к. выражаются через t линейно, , то все дифференциалы сохраняются, т.е. .

Экстремум функции нескольких переменных

Пусть функция определена в некоторой окрестности точки . Говорят, что у в точке максимум, если для будет . Если для будет , то максимум в точке называется строгим.

Необходимое условие экстремума: Пусть в точке у функции экстремум и в точке существует частные производные . Тогда .

Пусть существует . Т.к. , где . Т.к. у в точке экстремум, то будет .

Достаточное условие экстремума

Пусть дана квадратичная форма . Тогда называется положительно определённой, если для будет . называется неопределённой, если и .

Критерий Сильвестра: положительно определена, если отрицательно определена, если .

Пусть точка – стационарная для (т.е. ), и пусть в некоторой окрестности точки существуют и непрерывны все вторые частные производные . Если обозначить , то в точке у экстремум, если знакоопределена. Максимум, если отрицательна определена, минимум – если положительно и экстремума нет, если – знаконеопределённая квадратичная форма.

1. Применим к для точек M достаточно близких к точке формулу Тейлора: (полагая 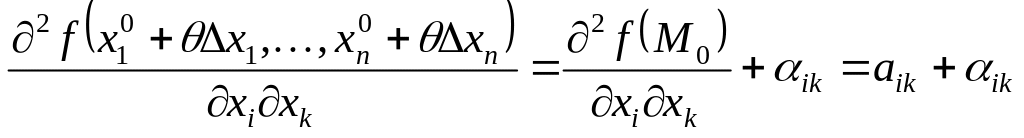, где при ) (положим , где ; тогда ) , где при . У нас рассматривается на множестве – сфере единичного радиуса с центром в начале координат. Эта сфера ограничена и замкнута, т.к. если точка – предельная для сферы, то существует последовательность и , откуда видно, что , т.е. что предельная точка принадлежит сфере. Пусть теперь, например, положительно определена. Тогда всюду на сфере , а по второй теореме Вейерштрасса, т.к. непрерывна, то . Вспомним, что , где при . Следовательно, при будет . Тогда при , т.е. при достаточно малых, будет , т.е. или , т.е. в точке минимум.

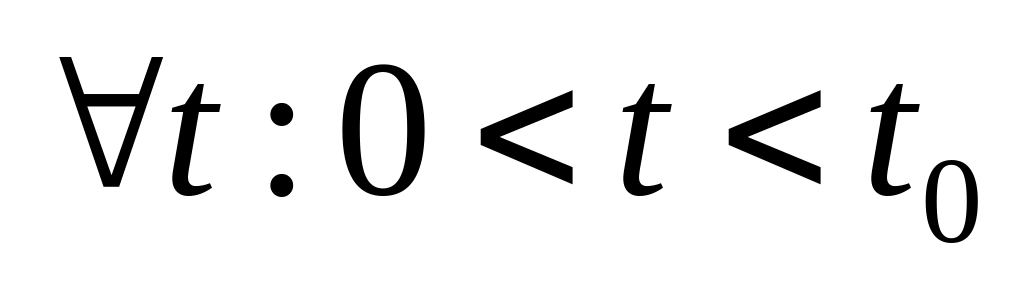2. Пусть теперь – знаконеопределённая форма, т.е. и , а . Положим . Тогда , где при , т.е. при . Т.к. при , то для будет . Но тогда для будет , следовательно, в точке экстремума нет.

Если для , то экстремума нет.

Пусть даны функции для которых существуют все для . Определитель называется определителем Якоби (якобианом) и обозначается: .

1. .

2. .

Теорема о неявной функции (для случая системы уравнений): Пусть заданы функции , причём в некоторой окрестности точки все дифференцируемы, все их частные производные I порядка непрерывны в точке и якобиан , а сами . Тогда для в окрестности точки пространства переменных существует и единственна система функций , которая является решением системы уравнений , причём в этой окрестности все непрерывны, дифференцируемы и .

Условный экстремум

Говорят, что решается задача на условный экстремум, если для функции ищутся точки, доставляющие экстремум этой функции среди точек, удовлетворяющих условиям (уравнения связи): .

Будем считать, что в необходимой нам области.

1-й метод: Если возможно, то из уравнений связи выражаем: , подставляем в и получаем и исследуем её на обычный экстремум.

2-й метод (только необходимые условия): Пусть выполнены условия теоремы о неявной функции для уравнений связи. Тогда хотя бы принципиально существуют функции , которые являются решением этого уравнения и нам достаточно исследовать на экстремум . Необходимое условие экстремума: , т.е. . По инвариантности формы первого дифференциала это условие можно записать в виде: . Продифференцируем уравнения связи: . Определитель этой системы относительно – это и поэтому эту систему можно разрешить относительно и все будут линейными функциями . Подставим в и получим: , т.к. независимы. В результате получим систему уравнений относительно неизвестных. – точка, подозрительная на экстремум.

3-й метод (метод множителей Лагранжа): (Этот метод представляет собой продолжение второго от первой системы). Умножим уравнения из системы на и сложим с . Получим: . Введём функцию (функцию Лагранжа) . Тогда имеем: . Подберём так, чтобы . Это возможно, т.к. , где  – определитель системы . Тогда при этих будет , что равносильно . Присоединяя условие , получим уравнений относительно .

Достаточный признак

Т.к. на множестве, заданном уравнениями связи , то достаточно рассматривать  вместо f. Имеем: . При этом , т.к. функция рассматривается на экстремум, следовательно, второй дифференциал можно писать по формуле для случая независимых переменных, т.к. и . Чтобы учесть множество, на котором рассматривается функция, дифференцируем уравнения связи: , выражаем через (это возможно, т.к. определитель системы ). Поставив в d, получим , которую и надо исследовать.

Теорема о неявной функции

Пусть задана функция , в некоторой окрестности точки дифференцируема, непрерывна и . Тогда для любого достаточно малого при уравнение имеет единственное решение, т.е. существует единственная функция , причём и непрерывна и дифференцируема.

1. Существование: Обозначим . Тогда и в некоторой окрестности точки дифференцируема и непрерывна. Пусть  – такая окрестность точки , в которой сохраняет знак, например, . Берём точки и лежат внутри шара . Т.к. на до функция возрастает по z (т.к. ), то . Т.к. в дифференцируема, то в  непрерывна, следовательно, у и существуют окрестности, где сохраняет знак. В частности, при будет . Убедимся, что при существует единственное решение уравнения при условии . Возьмём . Тогда ; на отрезке непрерывна и монотонна, т.к. , следовательно, на этом отрезке в единственной точке принимает значение . Обозначив найденные значения , мы и находим искомое решение , причём .

2. Непрерывность: т.к. любая точка 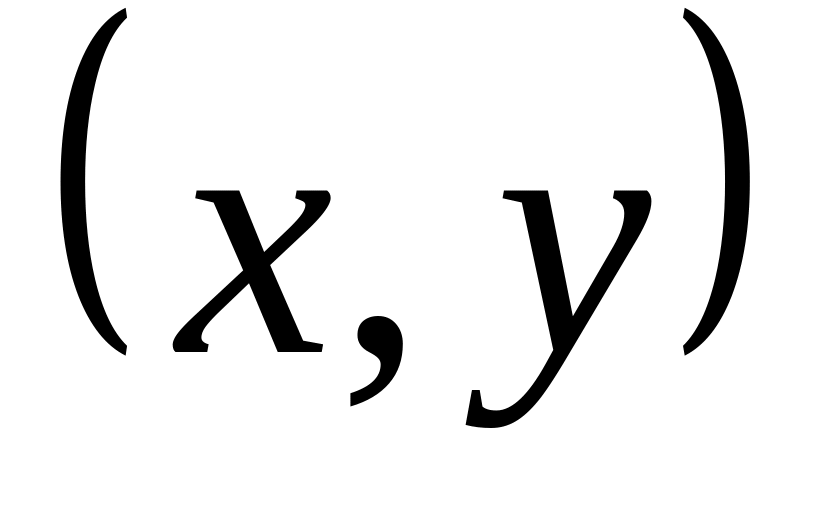из обладает точно такими же свойствами, что и (т.е. ), то доказательство достаточно провести для точки . А для этой точки непрерывность следует из самого построения. По любому достаточно малому найдено такое, что при будет а это и есть непрерывность .

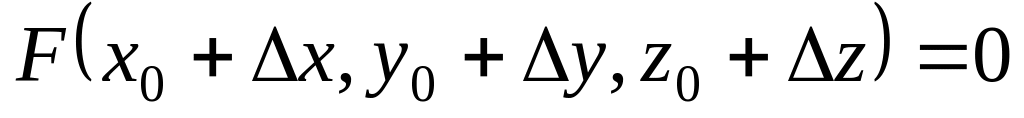3. Аналогично и дифференцируемость . Достаточно доказать для . Возьмём приращение x, y. Тогда функция получит приращение z, причём, т.к. непрерывны, то при . Кроме того, , откуда (т.к. – решение уравнения ). Но дифференцируема в точке , поэтому , где при , т.е. при . Т.к. , то при достаточно малых будет (т.к. ), откуда 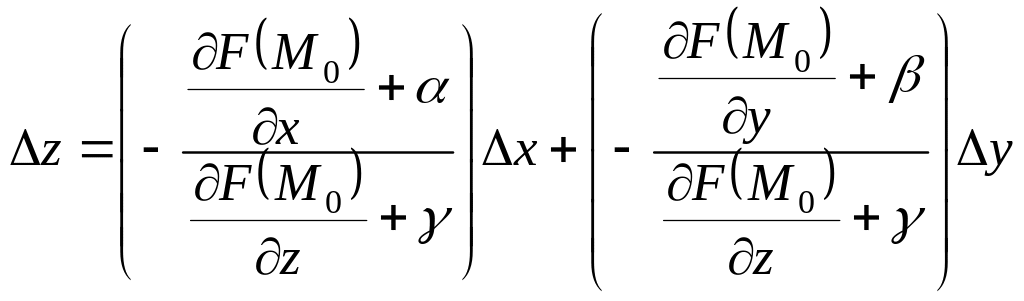. Заметим, что 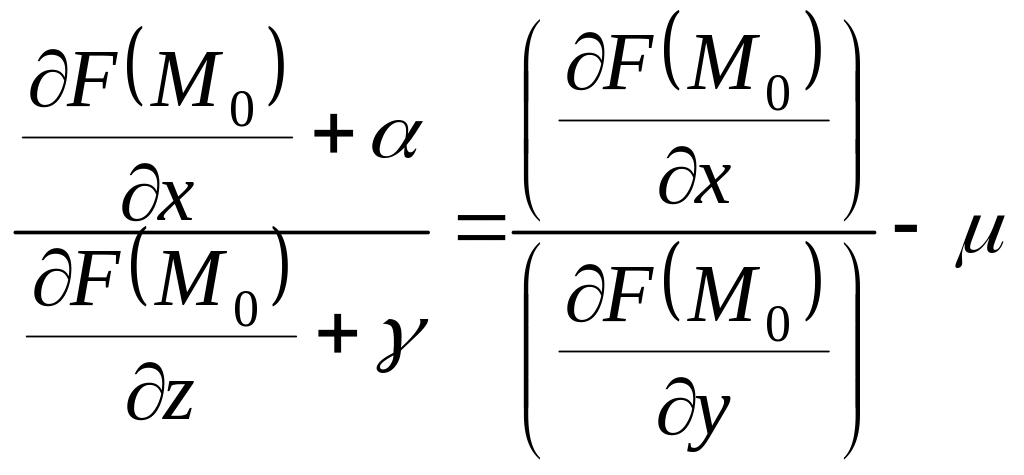, , где и при . Отсюда , что и означает дифференцируемость в точке , а, значит, и в любо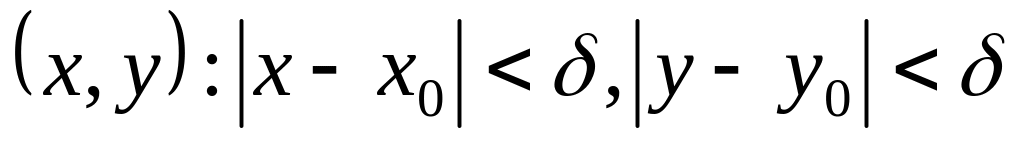й .

и .

Если заданы функции так: и , то .