Классы интегрируемых функций

Если непрерывна на , то интегрируема на .

Возьмём . По следствию из теоремы Кантора существует разбиение . Тогда по критерию функция интегрируема.

Пусть ограничена на и такова, что для существует конечная система непересекающихся отрезков , , содержащая внутри себя все точки разрыва и с общей длиной меньше . Тогда интегрируема на .

Ясно, что достаточно рассмотреть случай (если , то и интегрируема). Возьмём . В качестве части точек разбиения возьмём точки и , выбранные из условия, что содержат все точки разрыва , а . На отрезках , , …, непрерывна, следовательно, по следствию из теоремы Кантора, существуют точки такие, что . Все эти точки образуют разбиение a, , , , b. Тогда 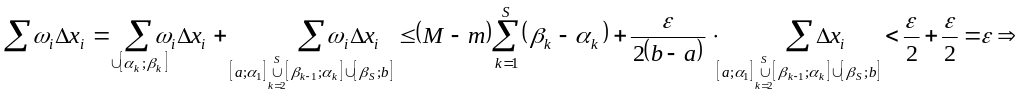по критерию интегрируемости функция интегрируема.

Если монотонна и ограничена на , то интегрируема на .

Пусть, например, не убывает на . Если ­ , то функция интегрируема. Пусть теперь . Возьмём и положим . Рассмотрим любое разбиение T с . интегрируема.

для на .

Т.к. , то . Т.к. , , то для и , откуда ­ . По определению supremum’a, .

Пусть интегрируема на , причём , когда и пусть непрерывна на . Тогда сложная функция интегрируема на .

Если , то и . Тогда интегрируема. Возьмём и . Т.к. непрерывна на , то равномерно непрерывна на , т.е. и для и таких, что . Т.к. интегрируема на , то для того же существует такое разбиение , что (здесь , ). Оценим для этого разбиения. Разобьём номера на два множества: , если и , если . Возьмём сначала . Тогда , т.к. на . Отсюда . Теперь рассмотрим и оценим . Имеем , откуда . Т.к. непрерывна на , то на . Тогда . Наконец, интегрируема на .

Следствия:

1. Если интегрируема на , то интегрируема на . (т.к. непрерывна везде).

2. Если интегрируема на и n – натуральное число, то интегрируема на . (т.к. непрерывна).

3. Если интегрируема на , то интегрируема на .

4. Если и интегрируема на , то интегрируема на .

Если и интегрируемы на , то .

Возьмём . По определению для всех разбиений T с при любом выборе точек будет , . Тогда для с при будет . Отсюда по определению интеграла .

Если и интегрируемы на , то интегрируема на .

Следует из того, что .

Если интегрируема на и , то интегрируема на ­ и .

Если , то и , т.е. для теорема справедлива. Пусть теперь . Возьмём . Тогда для с при будет . Тогда для с и будет .

Если и интегрируемы на ,  и , то .

Интегралы как функции множества

Если интегрируема на и , то интегрируема на .

Возьмём . Тогда существует разбиение . Добавим к T точки c и d: . Тогда – измельчение T и, значит, . Отсюда . Тогда по критерию функция интегрируема на .

Если интегрируема на и на , то интегрируема на .

Возьмём . Тогда существуют разбиения и ­ такие, что , . Объединим разбиения: . Тогда по критерию функция интегрируема.

Если интегрируема на и на , то .

Т.к. известно, что существует, то для любых разбиений T при любом выборе . Можно считать этот предел по определённому виду разбиений T, содержащих точку b. Тогда , причём по условию при , а . Отсюда .

Соглашения:

1. .

2. Если , то .

Если интегрируема на наибольшем из отрезков , и , то при любом расположении a, b и c будет .

Возьмём, например, . Тогда , , .