20. Полярная система координат. Переход в двойных интегралах от декартовой системы координат к полярной системе координат. Вычисление двойных инте­гралов в полярной системе координат.

Рассм сист ф-й: {x=ρcosφ, {y=ρsinφ (1), где 0≤φ≤2π, 0≤ρ≤+∞. Рассм что произойдет с этой системой φ=C. {х=ρcosC, {y=ρsinC. Почленно разделим 1 на 2 ур-е. y/x=tgC. Y=xtgC – семейство лучей,выходящих из начала координат (0,0) с угловым коэф k=tgC. Корд линии φ=C с помощью сист ф-й (1) переходит в семейство лучей, выходящих из (0б0) и угл коэф k=tgC.

ρ=С {x=Ccosφ, {y=Csinφ. Возв в ² и сложим. x²+y²=C² - cемейство концентрических окружностей с центром (0,0). R=C. Корд линии R=C с пом-ю (1) переходят в сем-во конц окр с центр в (0,0) и радиусом С. Зам-е: На практике дек корд т и полярные рассматр не на разных корд пл-тях, а на 1,т.е. совмещают пл-ти. Тогда φ и ρ являются криволинейными(полярн) координатами. Ф-лы (1) ф-лы связи между Декарт и полярн корд.

☼ Определитель 2го порядка вида J(φ,ρ)= наз-ся якобианом перехода от Декарт сист корд к полярной и обозначается J(φ,ρ). Вычислим его J(φ,ρ)= = - ρsin² φ- ρcos² φ= - ρ(cos²φ+ sin² φ)= - ρ. J(φ,ρ)= -ρ. Ф-ла перехода от дек корд к полярн имеет вид: f(x,y)dxdy= f(ρcosφ,ρsinφ) ρ dφdρ. (2) Якобиан перехода берется по модулю.

☼Обл D наз-ся правильной в напр полярн оси ρ, если луч,проходящий ч/з внутр т обл-ти пересекает границу этой обл-ти в 2х т – т входа и т выхода из обл-ти.

Если обл-ть D’ правильная в напр полярн оси ρ, то границу этой обл-ти можно выразить ур-ми: ρ=ρ₁(φ), ρ=ρ₂(φ), ρ₁(φ) ≤ρ₂(φ), φ [α,β].

Т если ф-я f(φ,ρ) непрерывна в обл-ти D’, к-я правильна в направлении полярной оси ρ, то f(φ,ρ) ρdφdρ= . Тогда из (2) получаем:

f(x,y)dxdy= f(φ,ρ) ρdφdρ=

20. Приложения двойных интегралов.

1) dxdy=S_D

2) f(x,y)dxdy=V_T, f(x,y)≥0, (x,y) D

3) m_D= μ(x,y)dxdy, μ= μ(х,у) – плотность распределения массы по плоской пластине D. Зам-я: Если пластина однородная, то пл-ть распределения массы, есть величина постоянная, μ(х,у)= μ=const

4) Статические моменты М_Х, М_Y пластины D относительно оси ох, оу.

М_Х= у μ(х,у)dxdy, M_Y=x μ(x,y)dxdy.

5) Площ пов-ти S с ур-м z=f(x,y) S= , частн произв ф-и z=f(x,y) – непрерывн, z=f(x,y) проэктир в D в пл-ти оху.

6) Координаты центра тяжести x_C= x μ(x,y)dxdy / μ(x,y)dxdy y_C= у μ(х,у)dxdy / μ(x,y)dxdy.

7) Момент инерции относит нач корд J₀, оси х - J_X, оси у - J_Y.

J₀= (x²+y²)μ(x,y)dxdy, J_X= y²μ(x,y)dxdy, J_Y= x²μ(x,y)dxdy.

27. Тройные интегралы и их свойства. Теорема о среднем. Вычисление тройных интегралов в декартовых координатах.

☼Обл-ть наз-ся кубируемой, если она имеет объем. Зам-е: в дальнейшем будем рассматривать только кубируемые обл-ти пр-ва.

Рассм огр кубир замкн обл-ть пр-ва V, в к-й определена ф-я u=f(x,y,z).

Огр замкн кубир обл-ть пр-ва – тело. Ф-я определена в V. Произв образ разбиваем тело V на n элементарн тел. (∆V₁),….( ∆V_n). Объем кажд тела: ∆V₁,…, ∆V_n. Диаметр обл-ти тела – наиб расст межд 2мя точками – также,как и в ∫∫.

В кажд элем теле выбираем диаметр d₁,…d_n. max(d₁,…d_n)=d. В кажд элем теле произвольн образом выбираем точку M_K­(x_K,y_K,z_K) (∆V_K), k=1n,

Произведение: f(x_K­,y_K,z_K)* ∆V_K, k=1n. Составим сумму: f(x₁,y₁,z₁) ∆V₁+…+f(x_n,y_nz_n)∆V_n= ∆V_K (1). Cумма (1) инт сумма для ф-и 3х переменных u=f(x,y,z) по телу V.

☼ Если при стремлении к 0 наиб из диаметров (d→0) существ конечн предел интегральной суммы (1) и предел не зависит ни от способа разбиения тела V на элементарные, ни от выбора точек в кажд элем теле, то он наз-ся тройным интегралом для ф-и 3х переем f(x,y,z) по телу V и обозначается: f(x,y,z)dxdydz. lim ∆V_K= f(x,y,z)dxdydz.

Теор Дост усл сущ-я ∫∫∫

Если ф-я 3х переем f(x,y,z) – непр в огр замкн кубируем обл-ти пр-ва V, тона интегрируема в этой обл-ти – существует ∫∫∫.

Физич смысл ∫∫∫ Если ф-я f(x,y,z) положительна в обл-ти V, то с физич т зрения ∫∫∫по телу V от ф-и f(x,y,z) – есть масса тела, занимающего объем V и имеющего переменную пл-ть распределения массы f(x,y,z) m= f(x,y,z)dxdydz.

п2 Св-ва тройных интегралов

1) dxdydz=V_T

2) [f₁(x,y,z)±f₂(x,y,z)]dxdydz= f₁(x,y,z)dxdydz± f₂(x,y,z)dxdydz Если ф-и инт по телу V,то их сумма тоже инт по V и выполняется ф-ла.

3)Если λ –действ ч-ло f(x,y,z) интегр по телу V, справедлива ф-ла: λ R, f(x,y,z) V, λf(x,y,z)dxdydz= λ f(x,y,z)dxdydz

4) Если тело V можно разбить на 2 тела V₁+V₂ и ф-я f(x,y,z) интегрируема по телу V и по каждому из V₁,V₂, то: f(x,y,z)dxdydz= f(x,y,z)dxdydz+ f(x,y,z)dxdydz

5) Если f(x,y,z) и g(x,y,z) интегр по V, причем выполняется соотношение f(x,y,z)≤g(x,y,z), то f(x,y,z)dxdydz ≤ g(x,y,z)dxdydz

6) Если ф-я f(x,y,z) инт по телу V, то | f(x,y,z)dxdydz |≤ |f(x,y,z)|dxdydz

7) Теорема о среднем Если ф-я f(x,y,z) непр в огр замкн обл-ти пр-ва V, то найдется т (x,y,z,) V, такая что f(x,y,z)dxdydz=f(x,y,z,)V_T.

Вычисление ∫∫∫ в Декарт сист коорд. ☼ Тело V наз-ся правильн в направлении оси oz, если выполняются условия: 1) любая прямая || оси oz и проходящая ч/з внутр т тела V пересекат границу этого тела в 2х точках – т. входа и т выхода из обл-ти тела; 2) проэкция тела V на пл-ть хоу – есть обл-ть D, правильная в направлении 1 из осей координат.

☼ Тело V наз-ся правильн в направлении оси ox, если выполняются условия: 1) любая прямая || оси ox и проходящая ч/з внутр т тела V пересекат границу этого тела в 2х точках – т. входа и т выхода из обл-ти тела; 2) проэкция тела V на пл-ть zоу – есть обл-ть D, правильная в направлении 1 из осей координат.

☼ Тело V наз-ся правильн в направлении оси oy, если выполняются условия: 1) любая прямая || оси o и проходящая ч/з внутр т тела V пересекат границу этого тела в 2х точках – т. входа и т выхода из обл-ти тела; 2) проэкция тела V на пл-ть хоz – есть обл-ть D, правильная в направлении 1 из осей координат.

Если тело V прав в напр оси аппликат (oz), то его границу можно выразить ур-ми z=h₁(x,y) – ур-е пов-ти, на к-й лежит т входа в обл-ть, z=h₂(x,y) – ур-е пов-ти на к-й лежит т выхода из обл-ти, h₁(x,y) ≤h₂(x,y), (x,y) D.

Т: Если ф-я f(x,y,z) непр по телу V, правильному в напр оси oz, D- проэкция тела (V) на пл-ть xoy, то f(x,y,z)dxdydz= dxdy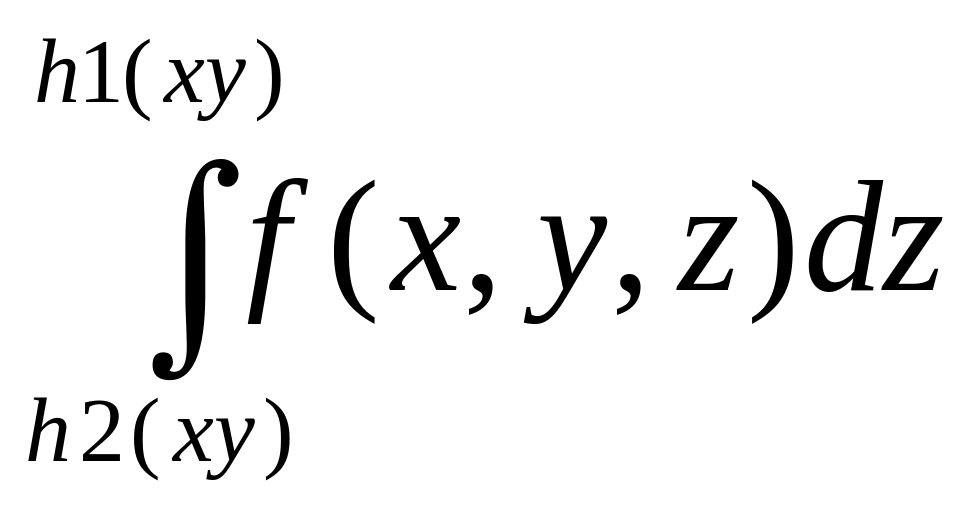 . Т.к. обл-ть D по опред – прав-я в напр 1 из осей корд, н-р, по оси у, то границу обл-ти D можно выразить ур-ми: y=g₁(x), y=g₂(x), где g_1­(x) ≤g₂(x) для х (a,b). Можем перейти к 3х кратному интегралу: f(x,y,z)dxdydz= dxdy = . Полярн или Декарт сист корд зависит от V.