
- •Е.А. Нурминский, л.Т. Ащепков, е.В. Трифонов Математические основы теории финансовых рынков
- •Основные инструменты
- •Облигации
- •Контракты
- •Опционы
- •Основные измерители финансовых рынков
- •Доходность
- •Дисконтирование и приведенная стоимость
- •Риск в финансовых моделях
- •Статическая теория ценообразования (capm)
- •Линия рынка ценных бумаг
- •Общая функция полезности
- •Аддитивность приведенной стоимости
- •Оценка управленческих решений
- •Арбитражная теория ценообразования
- •Оптимальное инвестирование
- •Статическая оптимизация портфеля
- •Основные понятия и обозначения
- •Инструменты или активы
- •Торговые стратегии
- •Мартингалы и возможности арбитража
- •Совершенные рынки и цены опционов
- •Цены и хеджирование опционов
- •Цены и хеджирование европейского опциона
- •Цена американского опциона
- •Биномиальная модель. Мартингализирующая мера
- •Биномиальная модель с точки зрения лп
- •Основные обозначения и постановка задачи
- •Биномиальный случай
- •Простейшее обобщение биномиальной модели: случай трех возможных состояний.
Общая функция полезности
К тем же соотношениям, что и в предыдущем разделе, приводят рассуждения для произвольной квадратичной функции полезности 7инвестора.
Чтобы
показать это, рассмотрим типичного
инвестора с портфелем рискованных
активов и банковским счетом ( безрисковым
активом ). Пусть в
![]() -ый
рискованный актив вложен капитал
-ый
рискованный актив вложен капитал
![]() и
его ( случайная ) доходность составляет
и
его ( случайная ) доходность составляет
![]()
![]() .
Стоимость банковского счета обозначим
через
.
Стоимость банковского счета обозначим
через
![]() ,
а его доходность ( гарантированную ) --
через
,
а его доходность ( гарантированную ) --
через
![]() .
.
В
этих условиях текущая суммарная стоимость
активов инвестора составляет
![]() ,
а его будущая стоимость представляет
собой
,
а его будущая стоимость представляет
собой
![]() .
Предположим, что инвестор оценивает
возможные последствия своих действий
с помощью функции полезности, квадратично
зависящей от величины капитала:
.
Предположим, что инвестор оценивает
возможные последствия своих действий
с помощью функции полезности, квадратично
зависящей от величины капитала:
|
(11) |
Предполагается, что
инвестор заинтересован в максимизации
![]() ,
т.е. вариант
,
т.е. вариант
![]() считается
предпочтительней
считается
предпочтительней
![]() ,
если
,
если
![]() .
Мы предполагаем специальную форму
квадратичной зависимости (11),
учитывая то, что
.
Мы предполагаем специальную форму
квадратичной зависимости (11),
учитывая то, что
функция должна быть вогнутой, для математической корректности задачи оптимизации,
на результат сравнения и
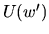 не
сказываются прибавление к функции
полезности постоянного слагаемого или
ее масштабирование с помощью некоторой
положительной константы.
не
сказываются прибавление к функции
полезности постоянного слагаемого или
ее масштабирование с помощью некоторой
положительной константы.
При многократном повторенни ситуации инвестор может быть заинтересован в максимизации средней полезности, получаемой от будущих доходов:

Обсуждение этого сведения можно найти в Приложении.
Для простоты рассмотрим сначала случай одного рискового актива и одного инвестора. Считая начальный капитал инвестора заданным, оптимальное поведение инвестора определим как решение задачи
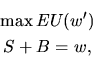
где
![]() и
и
![]() --
его капитал в акциях и банковском счете,
соответственно,
--
его капитал в акциях и банковском счете,
соответственно,
![]() --
капитал инвестора в следующий момент
времени. Доходность
рискового
актива предполагается случайной
величиной, доходность
безрискового
банковского актива неслучайна и известна
заранее.
--
капитал инвестора в следующий момент
времени. Доходность
рискового
актива предполагается случайной
величиной, доходность
безрискового
банковского актива неслучайна и известна
заранее.
Для того, чтобы решить эту задачу, необходимо составить функцию Лагранжа
![]()
где
![]() --
двойственная переменная, соответствующая
бюджетному ограничению, и приравнять
ее производные нулю:
--
двойственная переменная, соответствующая
бюджетному ограничению, и приравнять
ее производные нулю:
![]()
или
|
(12) |
Так как
![]() ,
то (12)
сводится к
,
то (12)
сводится к
![]()
Легко проверить, что
![]()
Следовательно
![]()
или
|
(13) |
Соотношение (13) справедливо для всех участников рынка, если предполагать их одинаково мотивированными, одинаково информированными и находящимися в однаковых экономических условиях. Поэтому, суммируя (13) по участникам, каждый из которых ассоциируется со своим , получаем
![]()
где
![]() и
сумма берется по всем участникам.
Стоимость всего рыночного запаса акций
и
сумма берется по всем участникам.
Стоимость всего рыночного запаса акций
![]() может
быть представлена как стоимость всего
рынка акций в предшествующий момент
времени, увеличенная в соответствии с
рыночной доходностью
:
может
быть представлена как стоимость всего
рынка акций в предшествующий момент
времени, увеличенная в соответствии с
рыночной доходностью
:
![]()
где
![]() --
переобозначение для
--
переобозначение для
![]() .
В результате получаем
.
В результате получаем
![]()
Аддитивность приведенной стоимости
С точки зрения практических экономистов большое достоинство CAPM заключается в том, что при оценке портфелей ценных бумаг она ведет к аддитивности приведенных стоимостей активов, составляющих данный портфель.
Пусть
портфель инвестора состоит из
бумаг
в объемах
![]() Тогда
его суммарная стоимость
Тогда
его суммарная стоимость
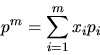
и доходность:
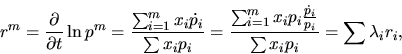
где
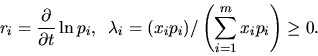
Очевидно
![]() Для
рыночного портфеля
Для
рыночного портфеля
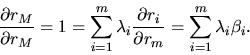
Рассмотрим,
не умаляя общности, пакет, состоящий из
двух ценных бумаг --
и
.
Доход от портфеля
![]() будет,
очевидно, равен сумме доходов от отдельных
акций:
будет,
очевидно, равен сумме доходов от отдельных
акций:
![]()
Вводя коэффициенты
доходности
![]() ,
относящиеся к доходности портфеля
и
отдельных активов
и
,
это равенство можно представить в виде:
,
относящиеся к доходности портфеля
и
отдельных активов
и
,
это равенство можно представить в виде:
|
(14) |
где
![]() --
приведенные стоимости акций
--
приведенные стоимости акций
![]() и
портфеля
.
и
портфеля
.
Дифференцируя
по
![]() получаем
получаем
![]()
или
|
(15) |
Теория CAPM дает
![]()
![]()
![]()
где
![]() --
рыночная премия за риск. Подставив эти
соотношения в (14),
получаем
--
рыночная премия за риск. Подставив эти
соотношения в (14),
получаем
![]()
Учитывая (15), получаем
![]()
или
![]()
что и требовалось доказать.
