Биномиальная модель с точки зрения лп

В настоящем разделе показывается, что расчет цены опциона для рынка с дискретным временем может быть проведен с помощью линейного программирования (ЛП). Такая формулировка задачи имеет многочисленные достоинства, поскольку линейное программирование достаточно хорошо апробировано на практике, а имеющееся программное обеспечение позволяет надежно решать задачи с тысячами ограничений [7]. На этом пути также возможно естественное обобщение биномиальной модели, а именно: можно рассмотреть модель, в которой цена акции на каждом этапе может изменяться по более чем двум вариантам. Ниже приводится постановка задачи ЛП для определения цены опциона и хеджирующей стратегии в полиномиальном случае, а также ее аналитическое (хотя и негладкое) решение для простейшего случая -- когда количество возможных состояний равно трем, а количество шагов по времени -- одному.

Subsections

• Основные обозначения и постановка задачи

• Биномиальный случай

• Простейшее обобщение биномиальной модели: случай трех возможных состояний.

Основные обозначения и постановка задачи

Рассмотрим следующую модель изменения цен акций. Предположим, что цена акции может меняться лишь в моменты времени

cледующим образом:

где - последовательность независимых одинаково распределенных случайных величин, принимающих значений с некоторыми вероятностями. Мы увидим, что как и в биномиальном случае [16], эти вероятности в конечный ответ для цены опциона не входят!

Пусть банковский счет растет по формуле сложных процентов:

Пусть инвестор, оперирующий на этом - рынке, в момент времени обладает начальным капиталом . Он может вложить некоторую его часть, , в акции, а оставшуюся, , поместить на банковский счет или вложить в «безрисковые» облигации:

Можно поставить следующую инвестиционную задачу: не привлекая дополнительных источников финансирования, довести в момент времени стоимость портфеля до величины не меньшей, чем заданная функция . ( Ее называют функцией выплаты ). Достичь этого инвестор может путем диверсификации портфеля: после того, как цена акции изменилась, он принимает решение о возможных изменениях значениий и .

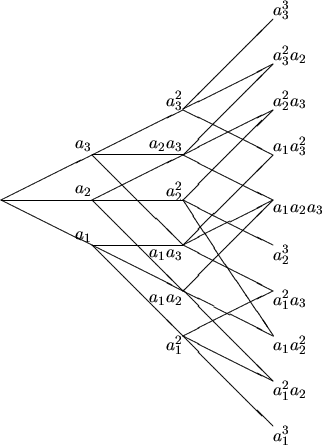
Все варианты цен акций можно наглядно представить в виде полиномиального дерева ( на рисунке 4.1.1 оно показано для случая, когда число вариантов изменения цен , а число шагов по времени  ). Каждому узлу дерева сопоставляется мультииндекс , если цена акции для этого узла есть . Таким образом, индекс показывает число случаев, в которых цена акции изменялась в раз ( до данного момента времени ). Отметим, что данный момент времени, в который происходит изменение цен акций, равен -- суммарному степенному показателю.

Figure: Пример полиномиального дерева.

Итак, пусть в момент времени инвестор находится в каком-то узле и принимает решение о диверсификации портфеля. Тогда условия самофинансируемости могут быть представлены в виде следующих равенств:

			(39)

Здесь в правых и левых частях равенств стоят величины капиталов соответственно до и после принятия решения в момент времени . Величина капитала при этом не меняется, меняется лишь его доля, вкладываемая в различные ценные бумаги ( отсюда и название «условия самофинансируемости» ). Через и обозначены доли капитала, вложенные в акции и облигации соответственно. Мы будем полагать также, что и .

Предположим теперь для простоты, что функция выплаты зависит лишь от стоимости акции в момент времени (это так, например, для весьма распространенного call - опциона с ). Тогда для выполнения инвестиционной задачи должны удовлетворяться следующие неравенства (хедж-условия):

(40)

где .

Число этих условий-неравенств совпадает, очевидно, с числом разбиений числа в упорядоченную сумму неотрицательных слагаемых, а это число, как известно из комбинаторики, равно . Если функция выплаты зависит от цены акции в более ранние моменты времени, то число хедж-условий должно быть увеличено очевидным образом.

Естественно постараться выполнить условия (41) и (42) при наименьшем начальном капитале . Подобная задача связана и с определением рациональной стоимости опциона европейского типа (см., например, обзор [12]).

Все вышесказанное делает естественным следующее.

Определение 16   Рациональная стоимость опциона в полиномиальной модели может быть определена как решение задачи минимизации функционала

(41)

при ограничениях, накладываемых условиями (41) и (42).

Поскольку функционал и условия являются линейными, то это задача линейного программирования.