24. Биномиальный закон распределения .

Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван «бино­миальным» потому, что правую часть равенства можно рассматривать как общий член разложения бинома Ньютона: (p+q)ⁿ=C_nⁿpⁿ+C_n^n-1p^n-1q+…+C_n^kp^kq^n-k+…+C_n⁰qⁿ

Пусть производится n независимых испытаний, в каждом из которых А может появиться или не появиться. Вероятность появления А во всех испытаниях постоянна и равна р. Рассмотрим в качестве дискретной случайной величины Х - число появлений А в этих испытаниях. Задача: найти закон распреде­ления величины X. Для этого требуется определить возможные значения Х и их вероятности. Возможные значения Х таковы: х₁=0, х₂=1, х₃=2,…х_n+1=n. Остается найти вероятности этих возможных значений, для чего восполь­зуемся формулой Бернулли: P_n(k)=C_n^kp^kq^n-k где k=0,1,2…n - аналитическое выражение искомого закона распределения.

Т .о., первый член разложения рⁿ опреде­ляет вероятность наступления рассматриваемого события n раз в n независимых испытаниях, 2й член определяет вероятность наступления события n-1 раз, и т.д., последний член qⁿ определяет вероятность того, что событие не появится ни разу. Биномиальный закон в виде таблицы:

25. Распределение Пуассона

Задача: найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз. !!допущение!!: про­изведение np сохраняет постоянное значение, а именно np=λ. Это означает, что среднее число появлений события при различных значениях n=const. Воспользуемся формулой Бернулли для вычисления вероятности:

но т.к. из формул комбинаторики известно, что число размещений 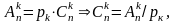при этом 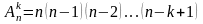. Тогда можно записать:

P_n(k)=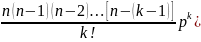 . Т.к. pn=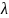 , то p=λ/n. Следовательно, P_n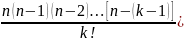(k)= )^k .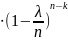

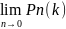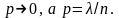Приняв во внимание, что n имеет очень большое значение, вместо Pn(k) найдем . При этом будет найдено лишь приближенное значение отыскиваемой вероят­ности; n хотя и велико, но конечно, а при отыскании предела мы устремим n к бесконечности. Заметим, что поскольку произведение nр – const, то при , вероятность Причём

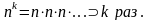
Итак, Pn(k)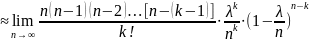

=

] =

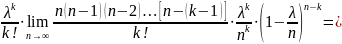
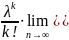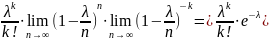
. Таким образом: P_n(k)=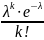 Эта формула выражает закон распределения Пуассона вероятностей массовых (n велико) и редких (р мало) событий.

Замечание. Имеются специальные таблицы, пользуясь кото­рыми можно найти Pn(к), зная k и λ.

Пример. На базу отправлено 5000 изде­лий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия. Решение. n=5000, p=0,0002, k=3. Найдем λ=np=5000*0,0002=1. По формуле Пуассона: P₅₀₀₀(3)=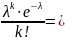 e^-1/3=0,06

26. Геометрическое распределение

Пусть производятся независимые испытания, в каждом из которых вероятность появления А равна p. Испытания заканчиваются, как только появится А. Обозначим через Х дискретную случайную величину — число испытаний, которые нужно провести до 1го появления А. Очевидно, возможными значениями Х являются натуральные числа 1.2… Пусть в первых k-1 испытаниях А не появлялось, а в k-м появилось. Вероятность этого события, по теореме умножения вероятностей независимых событий, P(Х=k)=q^k-1p. Полагая, что k=1,2,… получим геометрическую прогрессию с первым членом p и знаменателем q: p, qp, q²p,…,q^k-1p,… По этой причине распределение называют геометри­ческим. Легко убедиться, что ряд сходится и сумма его равна единице. Действительно, сумма ряда p/(1-q)=p/p=1.