26. Моменты распределения дискретных случайных величин

МОЖ и дисперсия являются част­ными случаями более общего понятия, называемого моментом рас­пределения случайной величины. В ТВ моменты служат для описания основных свойств распределения. Моментом распределения k-го порядка случайной величины X относи­тельно некоторой постоянной С называется МОЖ k-й степени отклонения X oт постоянной С: M(X – C)^k. Если постоянная С = 0, то момент называется начальным и обозначается: 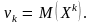Начальный момент k-го порядка абсолютной величины(модуля) называется абсолютным моментом: М (│Х│^k). Если в качестве С берется МОЖ m_х случайной величины X, т.е. центр ее распределения, то момент называется цент­ральным: При k=1 имеем: 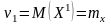, т.е. начальный момент 1го порядка есть МОЖ случайной ве­личины; 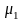= М(Х-m_х) = 0 — центральный момент 1го порядка, =0. При k=2: начальный момент второго порядка ν₂ = М(Х²) — МОЖ квадрата случай­ной величины X для вычис­ления дисперсии; μ₂ = М(Х— m_х)² = D(X) — центральный момент 2го порядка есть D случайной величины X. μ₃= М(Х— m_х)³; μ ₄ = М(Х— m_х)⁴. Иногда для более полной характеристики распределений использу­ются еще центральные моменты 3го и 4го порядков. Центральные моменты целесообразно вычислять, используя формулы, выражающие центральные моменты через начальные:

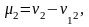
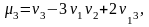
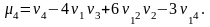
26. Коэффициент ассиметрии.

Коэффициент асимметрии является мерой симметричности ряда распределения относительно МОЖ. Коэффициент асиммет­рии - отношение центрального момента 3го порядка μ₃ к кубу СКО a=

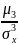
На рис1. приведены графики многоугольников распределения дискрет­ных случайных величин. Для случайной величины X, закон распределения вероятностей, которой приведен на рис. 1а, МОЖ будет рав­но m_х = 4. Из графика закона распределения следует, что он симметричен относительно МОЖ. Если для данного закона распределения вероятности посчитать μ₃ и коэффициент асимметрии, то увидим, что μ₃=0, а=0. То есть при 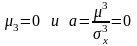график закона распределения является симметричным относительно МОЖ.

Для случайных величин, закон распределения вероятностей которых приведен на Рис. 1б и 1в, для МОЖй соответственно получим:

Законы распределения дискретных случайных величин с различными коэффициентами асимметрии: а) m_х = 4; б)m_х =4,7; в)m_х = 3,3

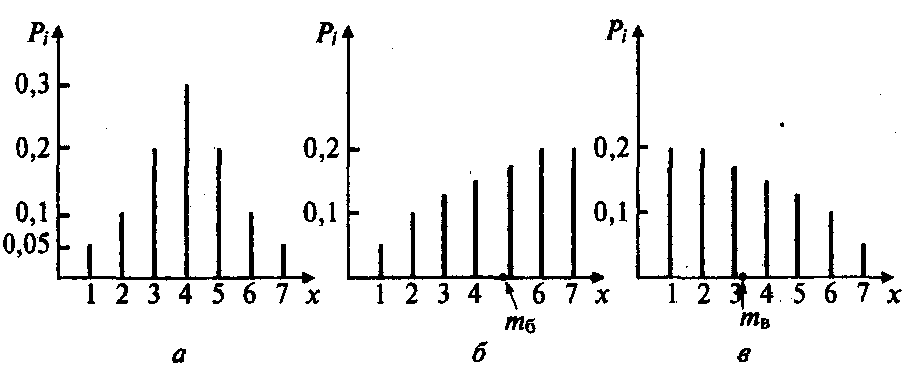
Из приведенных графиков 1б и 1в видно, что закон распределения вероят­ностей для этих случайных величин является несимметричным отно­сительно МОЖ . Для закона распределения вероятностей, на рис. 1в, μ₃ и a будут иметь отрицательные значения. Для закона распределения вероятностей, приведенного на рис. 1б, центральный момент 3го порядка и коэффициент асимметрии бу­дут иметь положительные значения.

26. Теорема Чебышева.

Сущность: отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеянно мало. Среднее арифметическое достаточно большого числа случай­ных величин с большой вероятностью принимает значе­ния, близкие к определенному постоянному числу, а именно к числу (М(Х1)+М(Х2)+…+М(Хn))/n (или к числу a в частном случае). Объясняется это тем, что отклонения каждой из величин от своих МОЖ могут быть и положительными, и отрицательными, а в среднем арифметическом они взаимно погашаются.

Значение для практики. Обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифме­тическое принимают в качестве искомого. При каких условиях этот способ измерения можно считать правильным? Ответ на этот вопрос дает теорема Чебы­шева.

Действительно, рассмотрим результаты каждого измерения как случайные величины Х₁,Х₂…Х_n. К этим величинам можно применить теорему Чебышева, если: 1) они попарно независимы, 2) имеют одно и то же МОЖ, 3) дисперсии их равномерно огра­ничены. 1е требование выполняется, если результат каж­дого измерения не зависит от результатов остальных. 2е требование выполняется, если измерения произ­ведены без систематических (одного знака) ошибок. В этом случае мат.ожидания всех случайных величин одинаковы и равны истинному размеру а. 3е требо­вание выполняется, если прибор обеспечивает определен­ную точность измерений. Хотя при этом результаты отдельных измерений различны, но рассеяние их огра­ничено. Если все указанные требования выполнены, мы вправе применить к результатам измерений теорему Чебышева: при достаточно большом n вероятность неравенства 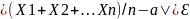как угодно близка к единице. Другими словами, при достаточно большом числе измерений почти достоверно, что их среднее арифметическое как угодно мало отли­чается от истинного значения измеряемой величины.

На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят о всей совокупности исследуемых объектов. Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон, наудачу отобранных из разных мест кипы. Т.е. можно заключить, что для практики теорема Чебышева имеет неоценимое зна­чение.