1.Понятие множества является одним из основных неопределяемых понятий математики. Подмножеством понимают совокупность (собрание, класс, семейство...) некоторых объектов, объединенных по какому-либо признаку. Так можно говорить о множестве студентов института, о множестве рыб в Черном море, о множестве корней уравнения х2+2х+2=0, о множестве всех натуральных чисел и т. д.

Объекты, из которых состоит множество, называются его элементами. Множества принято обозначать заглавными буквами латинского алфавита А, В,..., X, Y,..., а их элементы — малыми буквами a, b,... ...,х,у,...

Если элемент х принадлежит множеству X, то записывают х ÎX; запись хÏХ или х ÎX означает, что элемент х не принадлежит множеству X.

Множество, не содержащее ни одного элемента, называется пустым, обозначается символом Ø.

Элементы множества записывают в фигурных скобках, внутри которых они перечислены (если это возможно), либо указано общее свойство, которым обладают все элементы данного множества.

Например, запись А={1,3,15} означает, что множество А состоит из трех чисел 1, 3 и 15; запись А={х:0≤х≤2} означает, что множество А состоит из всех действительных (если не оговорено иное) чисел, удовлетворяющих неравенству 0 ≤ х ≤ 2.

Множество А называется подмножеством множества В, если каждый элемент множества А является элементом множества В. Символически это обозначают так АÌВ («А включено в В») или ВÉА («множество В включает в себя множество А»).

Говорят, что множества A и В равны или совпадают, и пишут А=В, если АÌВ и ВÌА. Другими словами ,множества, состоящие из одних и тех же элементов, называются равными.

Объединением (или суммой) множеств A и В называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств. Объединение (сумму) множеств обозначают AUВ (или А+В). Кратко можно записать АUВ={х:хєА или хєВ}.

Пересечением (или произведением) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит множеству А и множеству В. Пересечение (произведение) множеств обозначают А∩В (или А*В). Кратко можно записать А∩В={х:хєА и хєВ}

В дальнейшем для сокращения записей будем использовать некоторые простейшие логические символы:

ΑÞ ß — означает «из предложения α следует предложение ß»;

ΑÛ ß — «предложения α и ß равносильны», т. е. из α следует ß и из ß следует α;

" — означает «для любого», «для всякого»;

$ — «существует», «найдется»;

: — «имеет место», «такое что»;

→ — «соответствие».

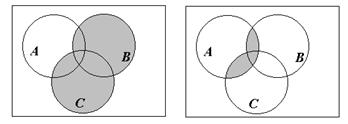
2.Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.

Операции над множествами рассматриваются для получения новых множеств из уже существующих.

О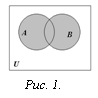 пределение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):

 

О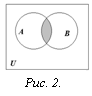 пределение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):

 

О пределение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):

 

О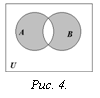 пределение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):

 

О пределение. Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А (рис. 5):

 

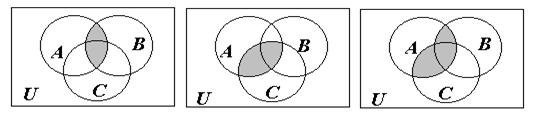
Пример 5. С помощью диаграмм Эйлера – Венна проиллюстрируем справедливость соотношения   (рис. 6).

Рис. 6.

Убедились, что в обоих случаях получаем равные множества. Следовательно, исходное соотношение справедливо.

3. Числовыми промежутками (интервалами) называют подмножества всех действительных чисел, имеющих следующий вид:

[a; b] = {х : α ≤ х ≤ b} — отрезок (сегмент, замкнутый промежуток);

(a; ) = {х : а < х < b} — интервал (открытый промежуток);

[a;b) = {х : а ≤ х < b};

(a; b] = {х : а < х ≤ b} — полуоткрытые интервалы (или полуоткрытые отрезки);

(-∞; b] = {х : х ≤ b}; [α, +∞) = {х : х ≥ α};

(-∞; b) = {х : х <b}; (а, +∞) = {х : х > а};

(-∞, ∞) = {х : -∞<х<+∞} = R — бесконечные интервалы (промежутки).

Числа a и b называются соответственно левым и правым концами этих промежутков. Символы -∞ и +∞ не числа, это символическое обозначение процесса неограниченного удаления точек числовой оси от начала 0 влево и вправо.

Пусть хо—любое действительное число (точка на числовой прямой). Окрестностью точки хо называется любой интервал (a; b), содержащий точку x0. В частности, интервал (хо-ε,хо+ε), где ε >0, называется ε-окрестностью точки хо. Число хо называется центром.

Если хÎ(х0-ε; х0 +ε), то выполняется неравенство x0-ε<х<х 0+ε, или, что то же, |х-х о|<ε. Выполнение последнего неравенства означает попадание точки х в ε -окрестность точки хо (см. рис. 97).

4. Множество рациональных чисел (лат. Ratio — отношение, деление, дробь) это числа, представленные обыкновенной дробью m/n , где m — целое число, а n — натуральное число.

При этом число m называется числителем, а число n — знаменателем дроби m/n .

Такую дробь следует интуитивно понимать, как результат деления m на n, даже если нацело разделить не удаётся.

Использовать множество рациональных чисел в реальной жизни можно для счёта частей некоторых целых, но делимых объектов, например, пирогов или других продуктов, разрезаемых на несколько частей перед употреблением, или для грубой оценки пространственных отношений протяжённых объектов.

Обозначается множество рациональных чисел - Q

Записать это множество можно в таком виде : Q={m/n, где m Є Z, n Є N } (где m принадлежит множеству целых чисел, а n - к множеству натуральных чисел.

Необходимо учитывать, что одинаковые дроби, такие как , например 3/4 и 9/12 , входят в это множество как одна дробь. Отсюда: множество рациональных чисел, это множество несократимых дробей с целым числителем и натуральным знаменателем.

5. Комплексные числа — это пара действительных чисел с заданными определенным образом операциями умножения и сложения. Комплексное число записывают как

Z=a+b*i

Таким образом, комплексное число задается двумя действительными числами. Если интерпретировать эти числа как декартовы координаты, то получим естественное соответствие комплексных чисел и точек на плоскости. Если в случае действительных чисел мы имели числовую прямую, то в случае комплексных чисел получаем числовую плоскость, которая называется комплексной плоскостью.

Число i=√-1 называется мнимой единицей. Можно рассматривать мнимую единицу как формальный объект, который имеет следующее свойство: I2-1

6. Комбинаторика - раздел математики, изучающей вопрос о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов). Правило суммы: Если некоторый элемент Х можно выбрать N способами, а элемент Y-M способами, причем любой способ выбора эл. Х отличается от любого способа выбора эл. Y, то выбор «Х или Y» можно сделать N+M способами. Правило произведения: Если элемент Х можно выбрать N способами, а элемент Y-M способами, причем любой способ выбора элемента Y, то выбор «X и Y» можно сделать M*N способами.

7.

8. Размещениями из n элементов по k называются соединения, которые можно образовать из n элементов, собирая в каждое соединение по k элементов, при этом соединения могут отличаться друг от друга как самими элементами, так и порядком их расположения.

Например, из 3 элементов (a,b,c) по 2 можно образовать следующие размещения: ab, ac, ba, bc, ca, cb.

Перестановки.Перестановками из n элементов называются соединения, каждое из которых содержит все n элементов, отличающихся поэтому друг от друга только порядком расположения элементов.

Например, из 3 элементов (a,b,c) можно образовать следующие перестановки: abc, bac, cab, acb, bca, cba.

Сочетания.Сочетаниями из n элементов по k называются соединения, которые можно образовать из n элементов, собирая в каждое соединение k элементов; при этом соединения отличаются друг от друга только самими элементами (различие порядка их расположения во внимание не принимается).

Например, из 3 элементов (a,b,c) по 2 можно образовать следующие сочетания: ab, ac, bc.

9, Бином Ньютона — формула разложения произвольной натуральной степени двучлена (а+b)ⁿ в многочлен. Каждый из нас знает наизусть формулы «квадрата суммы» (а+b)² и «куба суммы» (а+b)³, но при увеличении показателя степени с определением коэффициентов при членах многочлена начинаются трудности. Чтобы не совершить ошибку и применяется формула бинома Ньютона: В более общем виде формула коэффициентов в биноме записывается так: где k - порядковый номер слагаемого в многочлене. Напомним, что факториал — произведение натуральных чисел от 1 до n, то есть 1х2хЗх...хn — обозначается n!, например, 4!=1x2x3x4=24.

10,Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля. Имеет применение в теории вероятностей.

11. Случайные события.  Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти. Например если брошена монет она может упасть вверх гербом или вверх надписью. Поэтому событие ?при бросании монеты выпал герб? - случайное. Каждое случайное событие , в частности выпадение герба, есть следствие действия многих случайных причин (сила с которой брошена монета, форма монеты, вес и т.д.). Не возможно учесть влияние этих причин на результат, по сколку их число очень велико, по этому теория вероятностей не ставит перед собой задачу предсказать. Произойдет единичное событие или нет.  В дальнейшем, вместо того чтобы говорить ?совокупность условий S осуществлена?, будем говорить кратко ?произведено испытание?. Таким образом, события будет рассматривается как результат испытания.  2.2.Классификация случайных событий.  Полной группой событий называются несколько событий таких что в результате опыта непременно должно произойти хотя бы одно из них.  События называют несовместными, если появление одного из них исключает появления других событий в одном и том же испытании.  События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.