17

Вопросы по ТВиМС.

1. Цель: формирование знаний об основных понятиях ТВ, случайных величинах, их законах распределениях, об основах МС, которые необходимы для правильного применения методов ТВиМС при решении различных задач. Предмет: законо­мерности в случайных явлениях. Случайное явление — это явление, которое при неоднократном вос­произведении 1го и того же опыта протекает каждый раз несколько по-иному. Очевидно, что в природе нет ни 1го явления, в котором не присутствовали бы элементы случайности.

В настоящее время нет почти ни одной естест­венной и гуманитарной науки, в которой не применялись бы вероятностные методы. Они используются в физике, современной электротехнике и радиотехнике, современной экономике и социологии.

История.

1. 16-17вв. (Кардано, Гюйгенс, Паскаль, Ферма и др/) попытки создания теории азартных игр. Постепенно сформировались понятия «Вероятность», «Событие», «Частота» и др. Решались первые задачи ТВ – общей теории страхования, учёт заболеваемости населения, смертности, статистика несчастных случаев.

2. 17-18вв: Якоб Бернулли «Закон больших чисел» - 1е теоретическое обоснованием накопленных ранее фактов.. Моавр - обосновал так называемый Нормальный закон ( закон Гаусса); Лаплас - систематическое изложение основ ТВ, ряд идей для ТВиМС к вопросам практики, в частности к анализу ошибок наблюдений и измерений; Гаусс – метод обработки экспериментальных данных («метод наименьших квадратов»); Пуассон – доказал общую форму закона больших чисел, впервые применил ТВ к задачам стрельбы и др.

3) 18-19вв: учёные Петербургской математической школы: Буняковский– автор 1го курса ТВ на русском языке, создатель современной русской терминологии; Чебышев расширил закон больших чисел, ввёл метод моментов различных порядков; Марков заложил теорию, составляющую основное содержание современной ТВ; Ляпунов доказал центральную предельную теорему при очень общих условиях. В этот период теория вероятностей становится стройной математической наукой.

4) 19-20вв. Бернштейн - разработал 1ю законченную аксиоматику ТВ, расширил область применения теорем; Романовский –широко применяемые на практике законы статистики, Колмогоров - дал наиболее совершенное аксиоматическое построение ТВ, множество работ в области теории случайных функций, оценки эффективности сложных систем; Хинчин – множество работ в области исследования случайных процессов; Смирнов – работы в области МС и др. Зарубежные математики - Н.Винер, В. Феллер, Р.Фишер, Д.Нейман и др.

2. Событие - всякий факт, который в результате опыта может произойти или не произойти. Каждое событие обладает какой-то степенью возможности: одни — большей, другие — меньшей, причем для некоторых из этих событий мы сразу же можем решить, какое из них более, а какое менее возможно.

Совместные события - появление 1 из них не исключает появления другого в одном испытании. Несовместные - если появле­ние одного из них исключает появление других событий в одном и том же испытании. Пример - Брошена монета. Появление «герба» исключает по­явление «решки».

Если события, образующие полную группу попарно несовместны, то в результате испытания появится только 1о из этих событий.

Полная группа событий - если в результате испытания появится хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. Если события, образующие полную группу, попарно несов­местны, то в результате испытания появится одно и только одно из этих событий. Пример. Стрелок произвел выстрел по цели. Обязательно прои­зойдет одно из следующих двух событий: попадание, промах. Эти два несовместных события образуют полную группу.

3. Событие А независимое от события В, если вероят­ность события А не зависит от того, произошло событие В или нет. Событие А зависимое от события В, если вероят­ность события А меняется в зависимости от того, произошло собы­тие В или нет. Примеры. 1) Бросают 2 монеты; рассматриваются события: А — появление герба на 1й монете, В — появление герба на 2й монете. В данном случае вероятность события А не зависит от того, произошло событие В или нет.

Достоверное событие не может не произойти в результате эксперимента, оно происходит всегда. Невозможное событие - … Пример. Бросаем один раз игральную кость. Достоверное событие состоит в том, что при бросании игральной кости выпадет число очков, не меньше 1 и не больше 6.

Равновозможные - если есть осно­вания считать, что ни одно из них не является более возможным, чем другое. (Орел и решка). Противоположным событию A называется событие, состоящее в том, что событие A не произошло. Пример. Бросаем игральную кость. Событие A - выпадение четного числа очков, тогда событие - выпадение нечетного числа очков.

4. Результатом опыта может быть 1 или несколько взаимоисключающих исходов; эти исходы неразложимы и взаимно исключают друг друга. В этом случае говорят, что эксперимент заканчивается одним и только одним элементарным исходом. Благоприятствующее событие – событие, заключающееся в наступлении исследуемого события в испытании. Вероятность события - число, характеризующее степень воз­можности появления события. Вероятность (классическое) - отношение числа благоприятствующих исходов к общему числу всех равновозможных элементарных исходов. Предполагается, что эл.исходы не­совместны, равновозможны и образуют полную группу. P(A)=m/n. Свойства: 1. Вероятность достоверного события =1. Если событие достоверно, то каждый элементарный исход испытания благоприятствует собы­тию. В этом случае m = n, следовательно, P(A) = m/n=n/n=1. 2. Вероятность невозможного события =0. Если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае m = 0, тогда P(A) = m/n=0/n=0 3. Вероятность случайного события - положительное число, заключенное между нулем и еди­ницей. Cлучайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 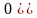, значит, , следовательно: 0<P(A)<1.

Причины ограниченности классического определения вероятности: 1) Классическое определение предпо­лагает, что число эл.исходов испытания ко­нечно. На практике это не всегда так. В таких случаях классическое определение неприменимо. 2) Очень часто невозможно представить результат испытания в виде совокупности эл.событий. 3) Трудно указать основания, позволяющие считать эл. события равновозможными. Обычно о равновозможности эл.исходов испытания говорят из соображений симметрии. Так, например, пред­полагают, что игральная кость имеет форму куба и изготовлена из однородного мате­риала. На практике такие задачи встречаются редко.

Аксиомы Колмогорова: 1)Каждому событию поставлено в соответствие неотрицательное действительное число. Это число называется вероятностью этого события. 2)Вероятность достоверного события =1. 3)Вероятность наступления хотя бы 1 из попарно несовместных событие = сумме вероятностей этих событий.

5. Относительная частота события - отноше­ние числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний. Формула: W(A) = m/n.

Сопоставление определения вероятности и относитель­ной частоты: определение вероятности не требует, чтобы испытания производились в действитель­ности; определение относительной частоты предпола­гает, что испытания были произведены фактически. Дру­гими словами, вероятность вычисляют до опыта, а относительную частоту—после. Кроме того, W обнаруживает свойство устойчивости. Это свой­ство состоит в том, что в разных опытах W изменяется мало, колеблясь около некоторого по­стоянного числа. Это постоянное число есть вероятность появления события. Т.о., если опытным путем установлена W, то полученное число можно принять за приближенное значение вероятности. Пример. По данным шведской статистики, относительная час­тота рождения девочек характеризуется сле­д. числами: … W колеблется около числа 0,482, которое можно принять за приближенное значение вероятности рождения девочек.

В качестве ста­тистической вероятности события принимают W или число, близкое к ней. Свойства вероятности, вытекаю­щие из классического определения, сохраняются и при статистическом определении.

Для существования статистической вероятности собы­тия А требуется: а) возможность производить неограниченное число испытаний, в каждом из которых событие А наступает или не наступает; б) устойчивость W появления А в различных сериях достаточно большого числа испыта­ний. Недостаток стат.определения - неоднозначность. Так, в при­веденном примере, в качестве вероятности события можно принять не только 0,4, но и 0,39; 0,41 и т. д.

6. Комбинаторика - раздел математики, изучающий количества комбинаций, подчиненных опред.условиям, которые можно со­ставить из элементов задан­ного конечного множества.

Перестановки (P_n)- комбинации, состоящие из одних и тех же п различных элементов и отличающиеся только порядком их расположения. Число всех возмож­ных перестановок P_n=n! Пример. Сколько трехзначных чисел можно составить из цифр 1, 2, 3? Р₃=3!=1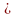 2 3=6.

Размещения(A_n^m) - комбинации, составленные из n различных элементов по т элементов, которые от­личаются либо составом элементов, либо их порядком. Число всех возможных размещений: A_n^m=n(n-1)(n-2)…(n-m+1) Пример. Сколько можно составить сигналов из 6 флажков различного цвета, взятых no 2? Решение. Искомое число сигналов A₆²=6*5=30.

Сочетания C_n^m - комбинации, составленные из n различных элементов по т элементов, которые отли­чаются хотя бы одним элементом. Число сочетаний: С_n^m=n!/(m!(n-m)!) Пример. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей? Решение. Искомое число способов C₁₀²=10!/2!(10-2)!=45 Числа размещений, перестановок и сочетаний связаны равенством A_n^m=P_m*C_n^m

Правило суммы: Если некоторый объект А может быть выбран из совокупности объектов m способами, а др.объект В может быть выбран n способами, то выбрать либо А, либо В можно m+n способами. Правило произведения: Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n спо­собами, то пара объектов (А, В) в указанном порядке может быть выбрана тп способами.

7. Сумма 2х событий А и В - событие С, состоящее в появлении хотя бы одного из событий А и В (или А, или В, или обоих). Например, если А — попадание в цель при 1м выстреле, В — попадание в цель при 2м выстреле, то событие С=А+В есть попадание в цель вообще, безразлично при каком — при 1м, при 2м или при обоих. Если события А и В несовместны, то появление обоих этих событий вместе отпадает, и сумма событий А и В сводится к появле­нию или А, или В. Сумма нескольких событий - событие, состоящее в появлении хотя бы одного из этих событий.

Произведение 2х событий А и В - событие С, состоящее в совместном появлении событий А и В. Например, если производится два выстрела по мишени и событие А — попадание при первом выстреле, событие В — попадание при втором выстреле, то С = АВ есть попадание при обоих выстрелах. Произведение нескольких событий - событие, состоя­щее в совместном появлении всех этих событий.

П ример записи сложного события с помощью операций суммы и произведения простых событий: Например, по мишени произвели 3 выстрела и рас­сматриваются след.эл.события:

Р ассмотрим сложное событие В, состоящее в том, что в результате 3х выстрелов будет одно попада­ние в мишень. Событие В можно представить в виде следующей комбинации элементарных событий:

Событие С, состоящее в том, что в мишени будет не менее двух попаданий, может быть представлено в виде:

Следствия: 1) А+А+…+А=А, 2) А* А*А*….*А=А; Если событие В есть частный случай события А, то справедливы следующие выражения: 1) А+В=А; 2) А_*В= В.

8. Теорема. Вероятность появления одного из 2х несов­местных событий, безразлично какого, равна сумме веро­ятностей этих событий: P(A+B)=P(A)+P(B). Для произвольного числа попарно несовместных собы­тий доказательство проводится методом математической индукции. Доказательство. n — общее число возможных элементарных исходов испытания; m₁ -­ число исходов, благоприятствующих А; m₂ — число исходов, благоприятствующих В. Число исходов, благоприятствующих наступлению либо А, либо В, равно m₁+m₂ тогда P(A+B)=(m₁+m₂)/n=m_1/n+m_2/n, где m_1/n=P(A) и m_2/n=P(B) Т.Е. P(A+B)=P(A)+P(B)

Следствие. Вероятность появления 1го из не­скольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий: P(A₁+A₂+…+A_n)=P(A₁)+P(A₂)+…+P(A_n). Доказательство. Рассмотрим три события: А, В и С. Т.к. рассматриваемые события попарно несов­местны, то появление одного из трех событий равносильно наступлению одного из двух событий, А+В и С, поэтому в силу указанной теоремы P(A+B+C) = P[(A+B)+C] = P(A+B)+P(C) = P(A)+P(B)+P(C). Пример. В урне 30 шаров: 10 красных, 5 синих, 15 белых. Найти вероятность появления цветного шара. Решение. Появление цветного шара означает появление либо красного, либо синего. Вероятность появления красного P(A)=10/30=1/3, вероятность появления синего P(B)=5/30=1/6. События А и В несовместны (появление шара 1го цвета исклю­чает появление шара др.цвета), поэтому при­менима теорема сложения. Искомая вероятность P(A+B)=P(A)+P(B)=1/3+1/6=1/2.

9. Теорема. Сумма вероятностей событий, образующих полную группу, =1: P(A₁)+P(A₂)+…+P(A_n)=1.

Доказательство. Т.к. появление 1го из событий полной группы достоверно, а вероятность досто­верного события равна единице, то P(A₁+A₂+…+A_n)=1. Любые 2 события полной группы несовместны, поэтому можно применить следствие теоремы сложения нескольких попарно несовместных событий: P(A₁+A₂+…+A_n)=P(A₁)+P(A₂)+…+P(A_n)=1. Значит, можно записать, что P(A₁)+P(A₂)+…+P(A_n)=1.

Пример. Институт получает контрольные работы из городов А, В и С. Вероятность полу­чения пакета из города А равна 0,7, из В - 0,2. Найти веро­ятность того, что пакет будет получен из города С. Решение. События «пакет получен из города А», «пакет получен из города В», «пакет получен из города С» образуют полную группу, поэтому сумма вероятностей этих событий равна единице: 0,7+0,2+p=1, отсюда искомая вероятность p=0,1.

10. Теорема сложения вероятностей противоположных событий. Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое принято обозначать Ā. Пример. Попадание и промах при выстреле – противоположные события. Теорема. Сумма вероятностей противоположных собы­тий равна единице: P(A)+P(Ā)=1. Доказательство. Противоположные события об­разуют полную группу, а сумма вероятностей событий, образующих полную группу, =1.

Замечание 1. Если вероятность одного из двух противоположных событий обозначена через p? То вероятность другого события обозначают через q. Тогда p+q=1.

Замечание 2. При решении задач на отыскание вероятности события A часто удобно сначала вычислить вероятность Ā, а затем искомую вероятность по формуле P(A)=1-P(Ā). Пример. В ящике имеется n деталей, из них m – стандартные. Найти вероятность того, что среди k наудачу извлеченных деталей есть хотя бы 1стандартная. Решение. События среди извлеченных «есть хотя бы 1 стандартная»(A) и «нет ни 1 стандартной» (Ā) - противоположные. Найдем P(Ā). Общее число способов, которыми можно извлечь k деталей равно C_n^k. Число нестандартных деталей равно n-m; из этого числа деталей можно C_n-m^k способами извлечь k нестандартных деталей. Поэтому вероятность того, что среди извлеченных k деталей нет ни одной стандартной равна P(Ā)= C_n-m^k/ C_n^k. Искомая вероятность P(A)=1- C_n-m^k/ C_n^k.

11. Принцип практической невозможности маловероятных событий

«Принцип практической невозможности маловероятных событий»: если случайное событие имеет очень малую вероятность, то можно считать, что в единичном испытании это собы­тие не наступит. Возникает вопрос: насколько малой должна быть вероятность, чтобы можно было считать невозможным появление в одном испытании? На этот вопрос нельзя ответить однозначно. Для различных задач ответы разные. Достаточно малую вероятность, при которой событие можно считать практически невозможным, называют уровнем значимости. На практике обычно принимают уровни значимости, заклю­ченные между 1-5%. Уровень значимости равный 0,01 называют однопроцентным; уровень значимости, равный 0,02, называют двухпроцентным, и т.д. Этот принцип позво­ляет делать предсказания не только о событиях, имею­щих малую вероятность, но и о событиях, вероятность которых близка к единице. Из принципа невозможности маловероятных событии вытекает следствие: если слу­чайное событие имеет вероятность, очень близкую к еди­нице, то практически можно считать, что в единичном испытании это событие наступит. Разумеется, и здесь ответ на вопрос о том, какую вероятность считать близ­кой к единице, зависит от существа задачи.

12. Независимые и зависимые события, условная вероятность события

Событие А независимое от события В, если вероят­ность события А не зависит от того, произошло событие В или нет. Событие А зависимое от события В, если вероят­ность события А меняется в зависимости от того, произошло собы­тие В или нет. Примеры. 1) Опыт состоит в бросании двух монет; рассматриваются события: А — появление герба на первой монете, В — появление герба на второй монете. В данном случае вероятность события А не зависит от того, произошло событие В или нет; событие А н е з а в и с и м о от собы­тия В. 2) В урне два белых шара и один черный; вынимают из урны по 1му шару; рассматриваются события: А—появление белого, В — появление белого во 2й попытке. Вероятность А до того, как известно что-либо о событии В, равна 2/3. Если стало известно, что событие В произошло, то вероятность события А становится равной 1/2, из чего заключаем, что событие А зависит от события В.

Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р(А/В) или Р_В(А). Другое определение условной вероятности: Р_А(В) – это вероятность В, вычисленную в предположении, что А уже наступило. Пример. В урне 3 белых и 3 черных шара. Из урны 2ды вынули по 1му шару. Найти вероят­ность появления белого шара при 2м испытании (событие В), если при 1м испытании был извлечен черный шар (событие А). Решение. После 1го испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность P_A(B)=3/5.

Условие независимости А от В можно записать как P(A/B)=P(A), а условие зависимости— P(A/B)≠P(A).

Общее определение условной вероятности: условная вероятность В при условии, что А уже наступило, по определению, равна Р_А (В)=Р(АВ)/Р(А) (Р(А)>0).

13. Теорема. Вероятность совместного появления 2х событии равна произведению вероятности одного из них на условную вероятность другого, при условии, что 1е уже наступило: P(AB)=P(A)*P_A(B) Доказательство. По определению условной веро­ятности P_A(B)=P(AB)/P(A), отсюда P(AB)=P(A)*P_A(B). Замечание. Применяя формулу к событию ВА, получим P(BA)=P(B)*P_B(A) или, поскольку событие ВА не отличается от события АВ, P(AB)=P(B)*P_B(A), значит справедливо P(A)*P_A(B)=P(B)*P_B(A). Т.е. порядок, в котором расположены собы­тия, может быть выбран любым, т.е. безразлично какое событие считать 1м, 2м и т. д. Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появи­лись: P(A₁A₂A₃…A_n)=P(A₁)*P_A1(A₂)*P_A1A2(A₃)…P_{A1A2A3…An-1}(A_n), где P_{A1A2A3…An-1}(A_n) – вероятность события A_n при условии, что события A₁A₂A₃…A_n-1 наступили. В частности для 3х событий P(ABC)= P(A)*P_A(B)*P_AB(C)

Пример . У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем 2й. Найти вероят­ность того, что 1й из взятых валиков—конусный, а второй— эллиптический. Решение. Вероятность того, что 1й валик окажется ко­нусным (А) P(A)=3/10, вероятность того, что 2й валик окажется эллиптическим (B), вычисленная в предположении, что первый валик конусный, т.е. условная вероятность PA(B)=7/9. По теореме умножения, искомая вероятность P(AB)=P(A)*P_A(B)=(3/10)*(7/9)=7/30.