26. Свойства 1,2 дисперсии

Свойство 1.: D(C)=0. Доказательство. По определению дисперсии, D(C)=M[C-M(C)²] Пользуясь свойством МОЖ (МОЖ постоянной равно самой постоянной), получим D(C)=M[(C-C)²]=M(0)=0. Свойство становится ясным, если учесть, что постоян­ная величина сохраняет одно и то же значение и рассея­ния, конечно, не имеет.

Свойство 2. Постоянный множитель можно выно­сить за знак D, возводя его в квадрат: D(CX)=C²D(X) Доказательство. По определению D имеем D(CX)=M{[CX-M(CX)]²}. Пользуясь 2м свойством МОЖ (постоянный множитель можно выносить за знак МОЖ), получим D(CX)=M{[CX-CM(X)]2} = M{C²[X-M(X)]²} = C²M{[X-M(X)]²}=C²D(X).

Теорема. Дисперсия числа появлений события А в n не­зависимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления со­бытия в одном испытании: D(X)=npq.

26. Свойства 3,4 дисперсии

Свойство 3. Дисперсия суммы 2х независимых случайных величин равна сумме дисперсий этих величин: D(X+Y)=D(X)+D(Y}. Доказательство. По формуле для вычисления дисперсии имеем D(X+Y)= M[(X+Y)²] – [M(X+Y)] Раскрыв скобки и пользуясь свойствами МОЖ суммы нескольких величин и произведе­ния 2х независимых случайных величин, получим

D(X+Y) = M[X²+2XY+Y²] - [M(X)+M(Y)]² = M(X²)+2M(X)*M(Y)+M(Y²) - M²(X)-2M(X)*M(Y)-M²(Y) = {M(X²)-[M(X)]²} + {M(Y²)-[M(Y)]²} + {M(Y²)-[M(Y)]²} = D(X)+D(Y).

Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин. Для произвольного числа слагаемых доказательство проводится методом мат. индукции.

Следствие 2. Дисперсия суммы постоянной вели­чины и случайной равна дисперсии случайной величины: D(C+X)=D(X) Доказательство. Величины С и Х независимы, поэтому, по 3у свойству, D(C+X)=D(C)+D(X) В силу первого свойства D (С) = 0. Следовательно, D(C+X)=D(X).

Свойство 4. Дисперсия разности 2х независимых случайных величин равна сумме их дисперсий: D(X-Y)=D(X)+D(Y) Доказательство. По 3му свойству D(X-Y)=D(X)+D(-Y), по 2му св-ву D(X-Y)=D(X)+(-1)²D(Y) или D(X-Y)=D(X)+D(Y).

26. Среднеквадратическое отклонение суммы независимых случайных величин.

Для оценки рассеяния возможных значений слу­чайной величины вокруг ее среднего значения кроме дис­персии служат и другие характеристики. К их числу относится среднеквадратическое отклонение. СКО случайной ве­личины Х называют квадратный корень из дисперсии: σ(X)= Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Т.к. среднее квадратическое отклонение равно квадратному корню из дисперсии, то размерность σ(Х) совпадает с размерностью X. Поэтому в тех случаях, когда жела­тельно, чтобы оценка рассеяния имела размерность слу­чайной величины, вычисляют среднее квадратическое от­клонение, а не дисперсию.

Теорема. СКО суммы конечного числа взаимно независимых случайных величин равно кв.корню из суммы квадратов СКО этих величин: σ(Х₁+…Х_n)=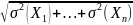 Доказательство. Обозначим через Х сумму рас­сматриваемых взаимно независимых величин: Х=Х₁+Х₂+…Х_n. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий слагаемых поэтому D(X)= D(Х₁)+D(Х₂)+…+D(Х_n) Отсюда 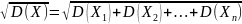или окончательно σ(X)=