26. Функция распределения

Дискретная случайная величина может быть задана перечнем всех ее возможных значений и их вероятностей. Однако такой способ задания неприменим, например, для непрерывных величин.

Поэтому вводят функции распределения вероятностей случайной величины. Пусть х—действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х т. е. вероятность события Х< x, обозначим через F(x). Разумеется, что если x изменяется, то изменяется и F(x), т.е. F(x) – функция от х. Функцией распределения называют функцию F (х), опре­деляющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х, т. е. F(x)=P(X< x).

Геометрически это равенство можно истолковать так: F(х) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х. Иногда вместо термина «функция распределения» используют термин «интегральная функция». Теперь можно дать более точное определение непре­рывной случайной величины: случайную величину назы­вают непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с не­прерывной производной.

26. Свойства функции распределения

Свойство 1. Значения функции распределения принадлежат отрезку 0 ≤ F(x) ≤ 1. Доказательство. Свойство вытекает из опреде­ления функции распределения как вероятности: вероят­ность всегда есть неотрицательное число, не превышающее единицы.

Свойство 2. F (х) —неубывающая функция, т. е. F(x₂)≥F(x₁) если x₁>x₂. Доказательство. Пусть x₁>x_2. Событие, состоящее в том, что Х примет значение, меньшее х₂, можно подразделить на 2 несовместных события: 1) Х примет значение, меньше х₁, с вероятность Р(Х<х₁); 2) Х примет значение, удовлетворяющее неравенству х₁≤Х<х₂, с вероятностью Р(х₁≤Х< х₂). По теореме сложения имеем: Р(Х<х₂)=Р(Х<x₁)+ P(x₁≤X<x₂)

Отсюда P(X< x₂) - P(X< x₁) = P(x₁≤X<x₂) или F(x₂)-F(x₁) = P(x₁≤X<x₂) Т.к. любая вероятность есть число неотрицательное, то F(x₂) – F(x₁) ≥0, или F(x₂) ≥ F(x₁).

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом ин­тервале: P(a≤X<b)=F(b)-F(a)

Это важное следствие вытекает из формулы, если положить х₂=b и х₁=а.

Следствие 2. Вероятность того, что непрерывная случайная величина Х примет 1о определенное значение, =0. Действительно, положив в формуле a=x₁, b=x₁+∆x, имеем P(x₁≤X<x₁+∆x)=F(x₁+∆x)-F(x₁). Устремим ∆x к 0. Т.к. Х – непрерывная случайная величина, то функция F(x) в точке х₁ разность F(x₁+∆x)-F(x₁) также стремится к нулю; следовательно, P(X-x₁)=0.

Используя это положение, легко убедиться, что P(a≤X<b) = P(a<X<b)= P(a<X≤b) = P(a≤X≤b). Например, равенство P(a<X≤b)=P(a<X<b) доказывается: P(a<X≤b) = P(a<X<b)+P(X=b) = P(a<X<b).

Ф 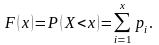ункция распределения может быть задана в табличном, графическом или аналитическом виде. Для дискретной случайной величины Х можно записать:

26. 3 Свойство функции распределения

Свойство 3. Если возможные значения случайной величины принадлежат интервалу (a,b), то: 1) F(x)=0 при х≤а; 2) F(x)=1 при x≥b. Доказательство. 1) Пусть х₁≤а. Тогда событие Х<x₁ невозможно, т.к. значений, меньших х1, величина Х по условию не принимает) и вероятность его =0.

2) Пусть х₂≥b. Тогда событие Х<х₂ достоверно (т.к. все возможные значения Х меньше х₂) и вероятность его равна единице.

Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси х, то спра­ведливы след. соотношения: ;

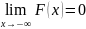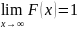
Для непрерывной случайной величины график расположен в полосе, ограниченной прямыми у==0, у=1 (1е свойство). При возрастании x на (a, b), в котором заключены все возможные значения случайной величины, график «поднимается вверх» (2е свойство). При x≤a ординаты графика =0; при x≥b ординаты

F(x)

графика =1 (3е свойство).

График функции распределения дискретной

слу­чайной величины имеет ступенчатый вид.

26. Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию f(x) - первую производную от функции распределения F(x): f(x)=F’(x). Из этого определения следует, что функция распре­деления является первообразной для плотности распре­деления. Для описания распределения вероятно­стей дискретной случайной величины плотность распре­деления неприменима.

С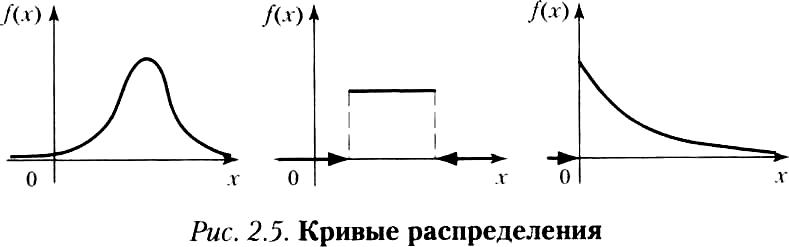 войство 1. Плотность распределения—не­отрицательная функция: f(x)≥0. Доказательство. Функция распределения — не­убывающая функция, следовательно, ее производная функция неотрицательная. Геометрически это означает, что точ­ки, принадлежащие гра­фику плотности распреде­ления, расположены либо над осью Ох, либо на этой оси.

График плотности распределения называют кривой распределения.

Свойство 2. Несобственный интеграл от плотности распределения в пределах от - ∞ до + ∞ =1:

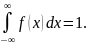
Доказательство. Несобственный интеграл выражает вероятность события, состоящего в том, что случайная величина примет значение, принадлежащее интервалу (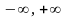 ). Очевидно, такое событие достоверно, следовательно, вероятность его =1. Геометрически это означает, что вся площадь криво­линейной трапеции, ограниченной осью Ох и кривой распределения, =1. В частности, если все возможные значения случайной величины принадлежат интервалу (а, b), то