31.4. Выборочные дисперсия и среднеквадратичное отклонение

В реальном эксперименте мы имеем дело с выборкой конечного объема, а не с генеральной совокупностью, подчиняющейся нормальному закону. Поэтому чтобы воспользоваться формулой для определения случайной доверительной погрешности результата измерения, необходимо найти оценку параметра и новые коэффициенты (которые в этом случае будут также зависеть от количества измерений ), соответствующие выборке конечного объема.

31.5. Среднеквадратичная ошибка среднего.

Допустим, что последовательных измерений некоторой величины дали значения

. (31.13)

При этом число не обязательно должно быть большим - в обычных экспериментах оно равно 5 - 10. В качестве наилучшего значения интересующей нас величины лучше всего взять среднее

. (31.14)

Требуется определить, какова ошибка в величине .

Ошибку -го измерения мы напишем в виде

, (31.15)

где - истинное значение измеряемой величины, которое, конечно, неизвестно. Тогда ошибка среднего дается выражением

. (31.16)

Теперь представим себе, что данные наблюдаются сериями по измерений в каждой, причем число таких серий велико. Вся совокупность измеренных значений характеризуется каким-то распределением со среднеквадратичным отклонением . В каждой серии имеется свое среднее значение, и совокупность всех таких средних характеризуется своим распределением со среднеквадратичным отклонением . В реальном эксперименте мы, конечно, имеем дело лишь с одной серией из измерений и одним средним значением. Но мы хотим подчеркнуть, что эта серия представляет собой случайную выборку из полной совокупности отдельных измерений, а среднее значение есть лишь одно значение из полной совокупности средних. Величина называется среднеквадратичной ошибкой среднего, и мы будем рассматривать ее как меру ошибки среднего значения.

Величины и связаны простым соотношением. Действительно, для одной серии из измерений имеем

. (31.17)

Следовательно

. (31.18)

Усредним это выражение по всем сериям. Среднее величины есть . Среднее каждого члена двойной суммы равно нулю, поскольку ошибки и независимы и в среднем равны нулю. Итак, мы получаем следующее равенство

. (31.19)

По определению

. (31.20)

Тогда равенство можно переписать в виде

, (31.21)

т.е. среднеквадратичная ошибка среднего из измерений в меньше среднеквадратичной ошибки отдельного измерения.

Величина зависит только от точности отдельных измерений и не зависит от их числа, тогда как величину можно уменьшить, увеличив . Но поскольку уменьшается всего лишь как , повторять много раз измерение одной и той же величины оказывается не очень выгодным. Лучше попытаться уменьшить , снизив , т.е. повысив точность измерений.

Хотя соотношение (31.21) имеет важное значение, но оно не позволяет нам вычислить , так как мы не знаем величины . Для этой величины лучше всего было бы взять значение

, (31.22)

но - ошибки относительно истинного значения и поэтому нам неизвестны. Данное затруднение можно обойти, если оперировать с остатками.

Для -го измерения остаток дается равенством

. (31.23)

В отличие от ошибки остаток - известная величина. Обозначим среднеквадратичное значение остатков через .

. (31.24)

Величина называется выборочным среднеквадратичным отклонением.

. (31.25)

Поэтому

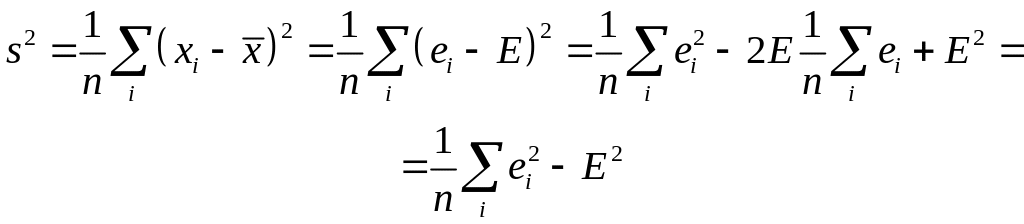. (31.26)

Все это относится к одной серии измерений. Усреднив, как и раньше, последнее равенство по большому числу серий, получим

, (31.27)

(31.28)

и

. (31.29)

Величина нам не известна. В качестве ее наилучшей оценки выберем . Подставляя эту величину в формулу и, извлекая квадратный корень, получаем

(31.30)

Таким образом, мы приблизительно выразили величину через известные нам величины.