
- •Раздел 10. Основы анализа экспериментальных данных
- •29.2. Классификация погрешностей
- •30. Обзор программного обеспечения для выполнения анализа, обработки и представления экспериментальных данных
- •30.1. Математические (символьные) вычисления
- •30.2. Расчеты и статистическая обработка результатов
- •30.2.1. MathCad
- •30.2.2. Matlab - Scilab - Octave
- •30.3. Построение графиков
- •30.3.1. Sigma Plot
- •30.3.2. Origin
- •30.3.3. Gnuplot
- •30.4. Работа с текстом
- •30.4.1. Ms Word
- •30.4.2. OpenOffice.Org
- •31. Анализ результатов измерений случайной величины.
- •31.1. Гистограмма. Эмпирическое распределение результатов наблюдений
- •31.2. Результат измерения. Доверительный интервал
- •31.3. Нормальное или гауссово распределение
- •31.4. Выборочные дисперсия и среднеквадратичное отклонение
- •31.5. Среднеквадратичная ошибка среднего.
- •31.6. Приборная погрешность. Класс точности прибора.
- •31.7. Сложение случайной и приборной погрешностей. Полная погрешность измерения
- •31.8. Запись и округление результата измерения
- •32. Ошибки косвенных измерений
- •32.1. Функция одной переменной
- •32.2. Функция нескольких переменных
- •32.3. Ошибки и методика эксперимента
- •33. Анализ результатов совместных измерений
- •33.1. Цель и особенности эксперимента по определению функциональной зависимости
- •33.2. Некоторые определения
- •33.3. Интерполяция
- •33.3.1. Глобальная интерполяция
- •33.3.2. Локальная интерполяция
- •33.3.2.1. Кусочно-линейная интерполяция
- •33.3.2.2. Интерполяция кубическими сплайнами
- •33.3.2.3. Интерполирование b-сплайнами
- •33.4. Экстраполяция
- •33.5. Сглаживание данных
- •33.6. Регрессия
- •33.6.1. Выбор вида математической модели
- •33.6.2. Метод наименьших квадратов.
- •33.6.2.1. Линейная зависимость.
- •33.6.2.2. Линеаризация
- •33.6.2.3. Полиномиальная регрессия
- •33.6.2.4. Регрессия линейной комбинацией функций
- •33.6.2.5. Регрессия общего вида.
33.6.2. Метод наименьших квадратов.
Усреднение несовместных решений избыточной системы уравнений может быть произведено различными способами (на глаз, методом медианных центров и т. д.). Наиболее мощный метод был разработан в 1795-180 гг. Лежандром и Гауссом и получил название регрессионного анализа, или метода наименьших квадратов (МНК). Но теперь благодаря возможности широкого доступа исследователей к вычислительной технике этот метод получил второе рождение. Дело в том, что вычисления по МНК черезвычайно громоздки. С появлением компьютеров положение коренным образом изменилось. Программы обработки данных МНК содержатся в математическом обеспечении любого компьютера. Поэтому практически надо только ввести свои данные в соответствии с этой программой и дождаться готового ответа. Но чтобы представлять себе, что делает с нашими данными компьютер по программам МНК, рассмотрим сущность МНК на примере простейших задач.
Задача
аппроксимации решается следующим
образом. В декартовой прямоугольной
системе координат наносят точки (xi,
yi).
По расположению этих точек высказывается
предположение о принадлежности искомой
функции к определенному классу функций.
Например, линейная функция
![]() ,
квадратичная
,
квадратичная
![]() и т.д. В общем случае
и т.д. В общем случае
![]() .
Неизвестные параметры функции
.
Неизвестные параметры функции
![]() определяются из требования минимума
суммы квадратов случайных ошибок, т. е.
минимума величины
определяются из требования минимума
суммы квадратов случайных ошибок, т. е.
минимума величины
![]() (33.12)
(33.12)
Величина
![]() называется также суммарной невязкой.
Необходимым условием минимума функции
нескольких переменных является обращение
в нуль частных производных невязки:
называется также суммарной невязкой.
Необходимым условием минимума функции
нескольких переменных является обращение
в нуль частных производных невязки:
 . (33.13)
. (33.13)
Отсюда и наименование: метод наименьших квадратов.
Решая систему уравнений (33.13), находим неизвестные параметры aj и тем самым полностью определяем функцию, которая наилучшим образом (в смысле наименьших квадратов отклонений от исходных точек или наименьшей суммарной невязки) аппроксимирует (приближает) искомую функцию .
33.6.2.1. Линейная зависимость.
Остановимся подробнее на линейной зависимости.
![]() . (33.14)
. (33.14)
Задача состоит в том, чтобы найти параметры m и c, при которых прямая наилучшим образом проходила бы через экспериментальные точки.
Линейная зависимость очень широко распространена в физике. И даже когда зависимость нелинейная, обычно стараются строить график так, чтобы получить прямую линию.
Допустим,
что имеется n
пар измеренных значений
![]() ,
,
![]() ,
…,
,
…,
![]() и предположим, что ошибки содержат лишь
величины y.
Такое предположение очень часто
оправдывается на практике. В противном
случае анализ существенно усложняется.
и предположим, что ошибки содержат лишь
величины y.
Такое предположение очень часто
оправдывается на практике. В противном
случае анализ существенно усложняется.
В случае параметров m и c отклонение в i -м измерении составляет
![]() . (33.15)
. (33.15)
Наилучшие значения m и c выбираются так, чтобы сумма
![]() (33.16)
(33.16)
была минимальной.
 . (33.17)
. (33.17)
Таким образом, искомые величины m и c получаются решением системы уравнений
 . (33.18)
. (33.18)
Второе уравнение показывает, что наилучшая прямая проходит через точку с координатами
 , (33.19)
, (33.19)
т.е. через центр тяжести всех экспериментальных точек. Из уравнений находим
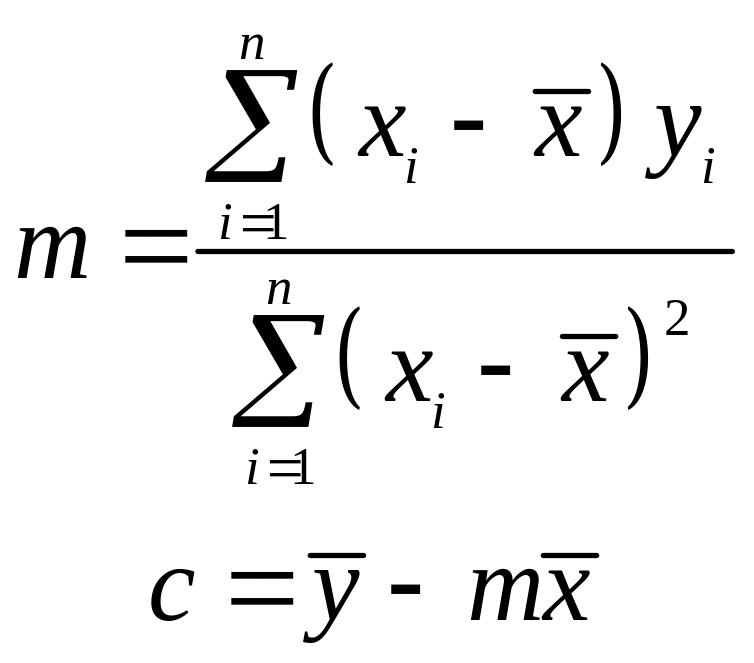 . (33.20)
. (33.20)
Результат обработки данных линейной зависимостью методом наименьших квадратов средствами Mathcad показан на рисунках 33.14 - 33.14.


Рис. 33.14: Метод наименьших квадратов. Аппроксимация линейной зависимостью средствами Mathcad.
