33.6.2.2. Линеаризация

Ввиду простоты расчетов, линейная зависимость используется довольно часто. Кроме того, многие функции, зависящие от двух параметров, можно линеаризовать путем замены переменных. Для этого необходимо подобрать такое преобразование исходной зависимости , в результате которого зависимость приобретает линейный вид . Далее решается задача линейной аппроксимации для новой зависимости и вычисленные коэффициенты b₀ и b₁ пересчитываются в коэффициенты a₀ и a₁.

Для ряда часто встречающихся двухпараметрических зависимостей возможные замены переменных приведены в Таблице 33.1.

Таблица 33.1.

Вид зависимости	Замена	Ограничения

33.6.2.3. Полиномиальная регрессия

Еще одним из наиболее распространенных вариантов обработки набора данных однофакторного эксперимента является аппроксимация полиномами.

Рис. 20: Реализация экспоненциальной регрессии.

Рассмотрим полином

, (33.21)

где - подгоночные параметры, m - степень полинома.

Метод наименьших квадратов требует, чтобы сумма квадратов отклонений, т. е. квадратов остатков, была минимальной. Она определяется следующим образом

, (33.22)

где n - число пар экспериментальных данных (x_i, y_i). Минимизируем R стандартным методом. Для этого определим производные по каждому из параметров и приравняем их к нулю.

. (33.23)

В результате мы имеем систему из m уравнений, линейных по неизвестным коэффициентам полинома

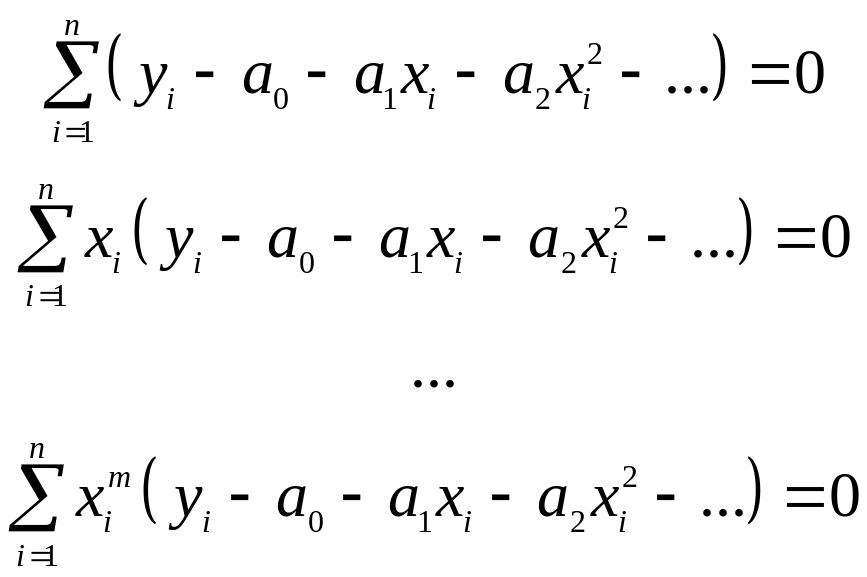, (33.24)

где суммирование производится по всем точкам. Преобразуя систему уравнений, получим

(33.25)

Систему линейных уравнений удобно представить в матричном обозначении Aa = b. Матрица A - квадратная симметричная матрица, a - вектор коэффициентов полинома, b - вектор свободных членов.

, (33.26)

, (33.27)

. (33.28)

Элементы матрицы A легко записать следующим образом

, (33.29)

где j - номер строки, k - номер столбца.

Подобным же образом запишем выражение для b

. (33.30)

Из линейной алгебры вы знаете, что решение для вектора a можно найти следующим образом

. (33.31)

Среднеквадратичная ошибка подгонки и ошибки подгоночных параметров определяются выражениями

. (33.32)

Качество аппроксимации полиномами различных степеней можно оценить сравнивая значения ѕ. Обратите внимание, что эта величина зависит от разности числа экспериментальных точек и числа подгоночных параметров.

33.6.2.4. Регрессия линейной комбинацией функций

В ряде случаев может оказаться, что данные необходимо аппроксимировать линейной комбинацией нескольких функций

. (33.33)

Полиномиальная регрессия является в этом смысле частным случаем. Определить коэффициенты перед функциями можно стандартным способом, минимизируя сумму квадратов остатков R.