33.3.2. Локальная интерполяция
33.3.2.1. Кусочно-линейная интерполяция
Простейшим
случаем локальной интерполяции является
линейная интерполяция, когда в качестве
интерполяционной функции выбирается
полином первой степени, т.е. узловые
точки соединяются прямыми линиями. Т.е.
для каждого интервала
строится зависимость
(33.5)
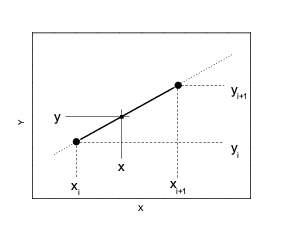
Рис. 33.4. Линейная интерполяция
Линейная интерполяция средствами MathCAD
Задача линейной интерполяции решается в MathCAD с помощью встроенной функции linterp(x,y,t), где
x - вектор действительных данных аргумента
y - вектор действительных данных значений того же размера
t - значение аргумента, при котором вычисляется интерполирующая функция.
При этом элементы вектора x должны быть определены в порядке возрастания, т. е. x1<x2<...<xn.
На практике использование линейной интерполяции по очевидным причинам весьма ограничено. Гораздо большее значение имеет приближение гладкими полиномиальными сплайнами, о котором мы поговорим в следующем разделе.
Рис. 33.5. Решение задачи кусочно-линейной интерполяции в MathCAD
33.3.2.2. Интерполяция кубическими сплайнами
Существенным недостатком кусочной интерполяции является то, что в точках стыка разных интерполяционных полиномов оказывается разрывной их первая производная. Этот недостаток устраняется при использовании особого вида интервальной интерполяции - интерполяции сплайнами (англ. spline - рейка, гибкая линейка).
Сплайн - это функция, которая на каждом частичном интервале представляется полиномом некоторой степени, а на всем заданном отрезке непрерывна вместе с несколькими своими производными.
В
настоящее время среди методов локальной
интерполяции наибольшее распространение
получила интерполяция кубическими
сплайнами. При этом строится интерполяционный
полином третьей степени, проходящий
через все заданные узлы и имеющий
непрерывную первую и вторую производные.
На каждом интервале
интерполирующая функция является
полиномом третьей степени
(33.6)
и удовлетворяет условиям
. (33.7)
Если всего n узлов, то интервалов - n-1. Значит, требуется определить 4(n-1) неизвестных коэффициентов полиномов. Условие прохождения интерполирующей функции через все узлы дает нам n уравнений. Условие непрерывности функции и ее первых двух производных во внутренних узлах интервала дает дополнительно 3(n-2) уравнений:
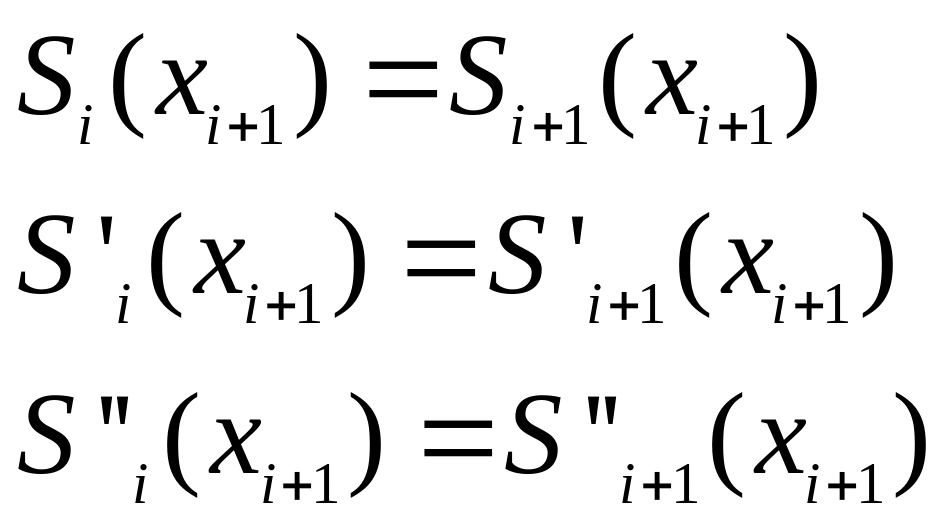. (33.8)
Всего имеем 4n-6 различных уравнений. Два недостающих уравнения можно получить, задавая условия на краях интервала. В частности, можно потребовать нулевой кривизны функции на краях интервала, т. е.
. (33.9)
Дополнительные условия могут быть и иными, поскольку их выбор, в общем случае, зависит от конкретной задачи.
Задавая различные условия на концах интервала, можно получить разные сплайны.
Интерполяция сплайнами имеет очень простую и наглядную физико-механическую аналогию. Если попытаться совместить упругую металлическую линейку с узловыми точками, то форма, которую примет в этом случае линейка будет совпадать с графиком кубического сплайна. Вне узловых точек, где линейка свободна, она описывается уравнением прямой. Соответствующее поведение сплайна обеспечивается условием на вторые производные, в связи с чем, его иногда называют условием свободных концов сплайнов. Если к свободным концам линейки подвесить небольшие грузы, то линейка деформируется и ее поведение вне узловых точек может быть описано, например, уравнением параболы. В этом случае условие будет совершенно иным (условие нагруженных сплайнов).
Сплайн-интерполяция средствами MathCAD
interp(s,x,y,t) - функция, аппроксимирующая данные векторов x, y кубическими сплайнами
s - вектор вторых производных, созданный одной из сопутствующих функций cspline, pspline, lspline
Функции cspline, pspline, lspline отличаются тем, что в окрестностях границ интервала точек интерполяции (и экстраполяции) осуществляется, соответственно, линейным, параболическим или кубическим полиномом. Внутри интервала точек интерполяция ведется кубическим полиномом во всех трех случаях.
x - вектор действительных данных аргумента, элементы которого
расположены в порядке возрастания
y - вектор действительных данных значений того же размера
t - значения аргумента, при котором вычисляется интерполирующая
функция.
Сплайн интерполяция в MathCAD реализована чуть сложнее линейной. Для применения функции interp необходимо предварительно определить первый из ее аргументов - векторную переменную s. Делается это при помощи одной из трех встроенных функций тех же аргументов (x,y).
Выбор конкретной функции сплайновых коэффициентов влияет на интерполяцию вблизи конечных точек интервала.
Обратите внимание, что вектор вторых производных может быть задан и непосредственно в скобках функции interp.
На первый взгляд, кривые, приведенные на рис. 6, кажутся различными. Однако, присмотревшись, вы увидите, что в области локализации экспериментальных точек они полностью идентичны, и различаются лишь уходящие на бесконечность продолжения кривых сплайна.
В каком случае интерполирующая кривая будет хорошо отображать изучаемую закономерность? Для этого должны выполняться два обязательных требования. Во-первых, погрешность должна отсутствовать или быть небольшой. Если это не так, то перед построением интерполирующего сплайна нужно подвергнуть данные обработке, которая уменьшит влияние погрешности. К примеру, можно задействовать алгоритмы сглаживания. Во-вторых, экспериментальные точки не должны быть слишком далеко друг от друга. Исходя из теоремы Котельникова, дискретизация должна быть в два раза меньше минимального элемента. То есть, если пик экстремума имеет ширину в 10 единиц, то экспериментальные точки нужно получить с шагом в 5 единиц, иначе экстремум может на интерполирующей кривой и не отобразиться.
Функции интерполяции - это чрезвычайно мощный и полезный инструмент.
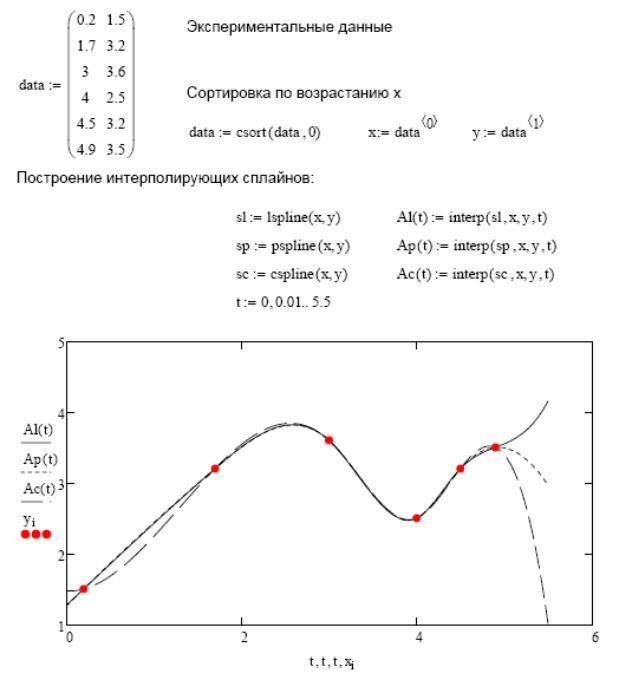
Рис. 33.6. Решение задачи сплайн - интерполяции в MathCAD