31. Анализ результатов измерений случайной величины.

Допустим, что мы проводим (без систематических ошибок) серию измерений одной и той же величины. Из-за наличия случайных ошибок отдельные значения и т.д. неодинаковы, и в качестве наилучшего значения искомой величины выбирается среднее арифметическое . Но вряд ли нам так сильно повезет, что величина окажется равной истинному значению, которое мы обозначим через . Мы хотим разобраться в том, насколько величина близка к . Конечно, истинная ошибка нам не известна. Иначе мы просто поправили бы на нужную величину и получили бы правильное значение . Мы можем сказать лишь следующее: имеется какая-то вероятность того, что лежит в каких-то пределах вблизи . Задача в том, чтобы найти, каковы эти пределы, соответствующие определенной вероятности.

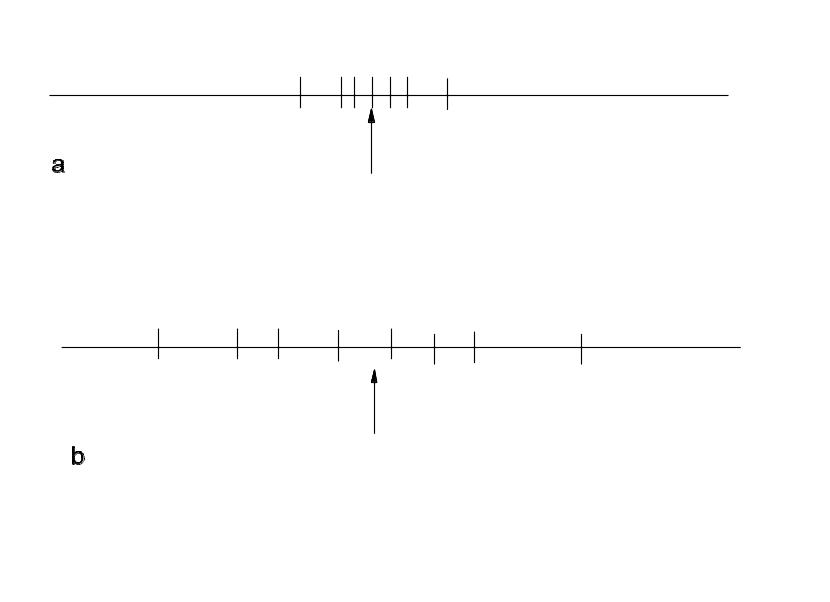
Рис. 31.1. Результаты многократного измерения одной и той же величины. В случае а среднее арифметическое должно быть ближе к истинному значению, чем в случае b.

Подход к решению этой задачи поясняется схемами на Рис. 31.1. В случае, представленном на Рис. 31.1a, величина должна, по-видимому, лежать довольно близко к , тогда как в случае, представленном на Рис. 1b, эта разница может быть большой. Иными словами, чем больше разброс результатов, тем больше должна быть ошибка в величине . Цель всей лекции - дать этому расплывчатому качественному утверждению четкое математическое количественное выражение. При этом мы будем предполагать, что систематические ошибки отсутствуют.

31.1. Гистограмма. Эмпирическое распределение результатов наблюдений

Результаты серии измерений одной величины можно наглядно представить, построив диаграмму, которая показывала бы, как часто получались те или иные значения. Такая диаграмма называется гистограммой. Чтобы построить гистограмму, мы просто разбиваем весь диапазон измеренных значений на равные интервалы и подсчитываем, сколько раз измеренная величина попадает в каждый интервал. Ширина интервалов может быть любой и выбирается так, чтобы это было удобно. Для примера в Таблице 31.1 приведены некоторые данные, а на рис. 31.2 изображена соответствующая гистограмма.

Таблица 31.1.

Результаты некоторых гипотетических измерений

Интервал, мм	Число случаев	Интервал, мм	Число случаев
9.9 – 10.1	1	10.7 – 10.9	4
10.1 – 10.3	3	10.9 – 11.1	5
10.3 – 10.5	7	11.1 – 11.3	2
10.5 – 10.7	9

Теперь представим, что измерения продолжают до тех пор, пока число измеренных значений не станет очень большим. Ширину интервалов можно сделать очень малой (при условии, что измерительный прибор обладает достаточной чувствительностью), и все же в каждом интервале будет много отсчетов. Если теперь вместо гистограммы построить график, который давал бы долю полного числа отсчетов , попадающих в каждый интервал, то получится гладкая кривая, которая называется кривой распределения. Мы можем ввести соответствующую функцию , так называемую плотность распределения, смысл которой состоит в том, что произведение дает долю полного числа отсчетов , приходящуюся на интервал от до . Иначе говоря, произведение есть вероятность того, что отдельное случайно выбранное значение измеренной величины окажется в интервале от до . Пока мы не будем касаться точного вида , укажем лишь, что типичная кривая распределения выглядит примерно так, как на рис. 31.3.

Рис. 31.2. Гистограмма данных, приведенных в Таблице 1.

Рис. 31.3. Типичная кривая распределения измеренных значений.

По определению, удовлетворяет условию

. (31.1)

Обратим внимание на бесконечные пределы у этого интеграла. В реальном эксперименте у нас не должны получаться значения измеряемой величины, сильно отличающиеся от истинного . Кроме того, многие из величин по самой своей сущности не принимают отрицательных значений. Поэтому любая функция , взятая нами в качестве плотности распределения, должна становиться очень малой при увеличении разности между и . Тогда не возникает никаких трудностей, связанных с бесконечными пределами интегрирования, которые берутся из соображений математического удобства.

В дальнейшем мы будем обозначать угловыми скобками усреднение по всей совокупности измеренных значений. Прежде всего, мы введем среднее значение для данного распределения

. (31.2)

Под средним мы всегда будем подразумевать среднее арифметическое, поскольку полное число измерений велико, а систематические ошибки отсутствуют, мы будем полагать, что совпадает с истинным значением .

Ошибка в измеренном значении равна

. (31.3)

Корень квадратный из среднего квадрата разности обозначается через и называется среднеквадратичным отклонением или среднеквадратичной ошибкой. Таким образом, величина определяется соотношением

. (31.4)

Величина называется дисперсией. Среднеквадратичное отклонение служит мерой ширины кривой распределения, т.е. разброса результатов измерений. При точных измерениях у кривой распределения будет узкий максимум вблизи значения и величина будет мала, а при грубых измерениях у нас будет большой разброс результатов относительно и среднеквадратичное отклонение будет велико.