Ответ №13
Производная обратной функции.
Теорема
4.3. Пусть функция y
= f(x)
определена, строго монотонна и непрерывна
в некоторой окрестности точки x0,
дифференцируема в точке x0,
причём производная f
'(x0)
0. Тогда в некоторой окрестности точки
у0(где
у0
= f(x0))
существует обратная функция x
= f
-1(y),
эта обратная функция дифференцируема
в точке у0,
и f
-1'(y0)=
.
Доказательство:
(рисунок)
Из условий теоремы следует: [a, b]: y = f(x) определена, строго монотонна и непрерывна на [a, b]. причём a < x0 < b. Поэтому, согласно теореме 3.5, множеством значений f(x), рассматриваемой на [a, b], является сегмент Y = [f(a), f(b)], на Y существует обратная функция x = f -1(y), строго монотонная и непрерывная. При этом y0 (f(a), f(b)). Зададим приращение y 0 аргументу обратной функции в точке y0. Обратная функция получит приращение х = f -1(y0 + y) - f -1(y0), причем х 0 в силу строгой монотонности обратной функции. Рассмотрим равенство:
=
.
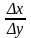(1)
Пусть y 0, тогда х 0 в силу непрерывности обратной функции. Но при х 0 знаменатель в правой части равенства (1) стремится к f '(x0), причем по условию f '(x0) 0. Поэтому при y 0 предел правой части равен . Следовательно при y 0 существует предел левой части равенства (1), то есть существует производная обратной функции в точке у0 и она равна : f -1'(y0)= .
Теорема доказана.
Лекция 12
Примеры:
y = sin x, - < x < . sin x f(x), x = arcsin y. arcsin y f-1(y) x (- , ) выполнены все условия теоремы 4.3
(arcsin
y)'
=
=
=
=[где
sin2
x
y2]
=
.
(arcsin
x)'
=
,
-1 < x
< 1.
При х +1 (-1): (arcsin x)' . В таком случае говорят, что функция имеет в данной точке бесконечную производную. Геометрически это означает, что график имеет в данной точке вертикальную касательную.
(рисунок)
(arccos x)' = - -докажите сами.
y = tg x на - < x <
x = arctg y. x (- , ) выполнены все условия теоремы 4.3
(arctg
y)' =
= cos2
x =
=
;
(arctg x)' =
.
(arcctg x)' = - - докажите сами.
Производная сложной функции.
Рассмотрим сложную функцию: y = f(t), где t = (x), то есть y = f((x)) F(x).
Теорема 4.4. Пусть функция t = (x) дифференцируема в точке х0, а функция y = f(t) дифференцируема в точке t0, где t0 = (х0). Тогда сложная функция F(x) = f((x)) дифференцируема в точке х0, и имеет место формула F'(х0) = f'(t0)'(х0) = f'((х0))'(х0).
Доказательство:
Нужно доказать, что приращение функции y = F(x) = f((x)) в точке х0 можно представить в виде: y = f'(t0)'(х0)x + (x)x, (1), где (x) 0 при x 0. (0) = 0. Зададим в точке х0 приращение аргумента х, равное x. Тогда функция t = (x) получит приращение t = ( х0 + х) - (х0). Так как t = (x) дифференцируема в точке х0 +, то t можно представить в виде : t = '(х0)x + (x)x. (2), где (x) 0 при x 0. (0) = 0. Приращению t соответствует приращение y = f(t0+t) + f'(t0), функции y = f(t). Так как y = f(t) дифференцируема в точке t0, то y можно представить в виде:
y = f'(t0) t + (t)t. (2), где (t) 0 при t 0. (0) = 0. (3)
Подставляя (2) в (3), получим:
y = f'( t0 )('(х0)x + [f'(t0)(x) + '(х0) + (x)]x, где [f'(t0)(x) + '(х0) + (x)] (x).
Очевидно, что (x) 0 при х 0, х 0.
Тем самым доказано равенство (1), и, значит, 4.4 доказана.
Примеры:
y = x ( - любое вещественное число, x > 0). x = eln x = e , где t = ln x ( ln x (x))
По теореме 4.4 получаем:
(x)' =(e)'( ln x)'= (e) = x-1. (e=х), = х). (x)' = x-1.
В
частности, если
=
,(
)'=
x-1/2=
.
Если
= -1, то
=
-1x-2
= -
.
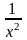Из правил и формул дифференцирования следует, что производная любой элементарной функции снова есть элементарная функция. Иными словами, класс элементарных функций замкнут относительно операции дифференцирования.
y = arccos (arctg ex )
y'
=
(-sin
(arctg ex))
ex
=
-tg(arctg ex)
=-
.
y
=[u(x)]v(x).
y =evlnu.
y = u(xv)'
= evlnu.(v
ln u)' = uv(v'ln
u + v
u')
= uvln
u v' + vuv-1u'
(uv)'
= (uv)'
+
(uv)'