Ответ №33

Пусть функция у=ƒ(х) определена на отрезке [а; b], а < b. Выполним следующие действия.

1. С помощью точек х₀=а, x_1, х_{2, ...,} х_n = В (х₀ <x₁ < ...< х_n) разобьем отрезок [а, b] на n частичных отрезков [х₀;х₁], [x₁; х₂],..., [х_n-1,х_n] (см. рис. 167).

2. В каждом частичном отрезке [x_i-1;x_i], i = 1,2,...,n выберем произвольную точку с_i є [x_i-1; x_i] и вычислим значение функции в ней, т. е. величину ƒ(с_i).

3. Умножим найденное значение функции ƒ (с_i) на длину ∆x_i=x_i-x_i-1 соответствующего частичного отрезка: ƒ (с_i) • ∆х_i.

4. Составим сумму S_n всех таких произведений:

Сумма вида (35.1) называется интегральной суммой функции у = ƒ(х) на отрезке [а; b]. Обозначим через λ длину наибольшего частичного отрезка: λ = max ∆x_i(i = 1,2,..., n).

5. Найдем предел интегральной суммы (35.1), когда n → ∞ так, что λ→0.

Если при этом интегральная сумма S_n имеет предел I, который не зависит ни от способа разбиения отрезка [а; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции у = ƒ(х) на отрезке [а; b] и обозначается Таким образом,

Числа а и b называются соответственна нижним и верхним пределами интегрирования, ƒ(х) — подынтегральной функцией, ƒ(х) dx — подынтегральным выражением, х — переменной интегрирования, отрезок [а; b] — областью (отрезком) интегрирования.

Функция у=ƒ(х), для которой на отрезке [а; b] существует определенный интеграл называется интегрируемой на этом отрезке.

Сформулируем теперь теорему существования определенного интеграла.

Теорема 35.1 (Коши). Если функция у = ƒ(х) непрерывна на отрезке [а; b], то определенный интеграл

Отметим, что непрерывность функции является достаточным условием ее интегрируемости. Однако определенный интеграл может существовать и для некоторых разрывных функций, в частности для всякой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва.

Укажем некоторые свойства определенного интеграла, непосредственно вытекающие из его определения (35.2).

1. Определенный интеграл не зависим от обозначения переменной интегрирования:

Это следует из того, что интегральная сумма (35.1), а следовательно, и ее предел (35.2) не зависят от того, какой буквой обозначается аргумент данной функции.

2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:

3. Для любого действительного числа с.

Ответ №34

1. Линейность. Если функции y = f(x), y = g(x) интегрируемы по отрезку [a,b] , то по этому отрезку интегрируема их линейная комбинация A f(x) + B g(x) (A, B = const), и  .  Док-во: для любого разбиения отрезка и любого выбора точек   выполняется   . Перейдем в этом равенстве к пределу при  . Так как существуют пределы интегральных сумм, стоящих в левой части равенства, то существует предел линейной комбинации этих сумм, следовательно, существует предел правой интегральной суммы, откуда следует истинность и утверждения, и равенства.  2. Аддитивность. Если y = f(x) интегрируема по отрезку [a,b] и точка c принадлежит этому отрезку, то  .  Док-во. Если f(x) удовлетворяет условиям интегрируемости по отрезку [a,b], то она удовлетворяет условиям интегрируемости по отрезкам [a,c] и [c,b]. Будем брать такие разбиения отрезка [a,b] , чтобы точка c являлась одним из узлов x_i: c = x_i0, . Тогда . В этом равенстве первая сумма справа - интегральная сумма для  , вторая - для  . Переходим к пределу при  . Пределы для всех трёх сумм существуют, и  .  Свойство аддитивности остаётся верным при любом расположении точек, если только функция интегрируема по самому широкому интервалу. Пусть, например, c < b < a, и f(x)интегрируема по [c, a]. Тогда, по доказанному,  . Отсюда и из определения интеграла для случая, когда нижний предел больше верхнего, следует, что  . 

«Теорема о среднем».

Если функция ƒ(х) непрерывна на отрезке [а; b], то существует тонка с є [а; b] такая, что

▼По формуле Ньютона-Лейбница имеем

где F'(x) = ƒ(х). Применяя к разности F(b)-F(a) теорему Лагранжа (теорему о конечном приращении функции), получим

F(b)-F(a) = F'(c)•(b-а) = ƒ(с)•(b-а).▲

С войство 5 («теорема о среднем») при ƒ (х) ≥ 0 имеет простой геометрический смысл: значение определенного интеграла равно, при некотором с є (а; b), площади прямоугольника с высотой ƒ (с) и основанием b- а  (см. рис. 170). Число

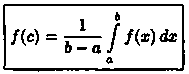
называется средним значением функции ƒ(х) на отрезке [а; b].

6. Если функция ƒ (х) сохраняет знак на отрезке [а; b], где а < b, то интеграл имеет тот же знак, что и функция. Так, если ƒ(х)≥0 на отрезке [а; b], то

▼По «теореме о среднем» (свойство 5)

где с є [а; b]. А так как ƒ(х) ≥ 0 для всех х  [а; b], то и

ƒ(с)≥0, b-а>0.

Поэтому ƒ(с)•(b-а) ≥ 0, т. е. ▲