Кліткове розбиття поверхні Орієнтовні поверхні
Система кривих здійснює кліткове|кліткове| розбиття поверхні, якщо виконані наступні|слідуючі| умови:
α) кожна з кривих γі (t = 1, 2, ..., k) гомеоморфна| замкненому відрізку;
β) дві криві γі, γj (i ≠ j) мають не більше однієї спільної|спільної| точки|точки|;
γ) з|із| кожного кінця кривої γі виходить щонайменше ще одна крива γj, i≠j;
δ) криві γ1, γ2,…, γk розбивають поверхню S на клітки|клітини| G1, G2, ..., Gf; кожна з кліток|клітин| Gі гомеоморфна| відкритому|відчиненому| кругу|колу|, дві клітки|клітини| Gі і gj (i ≠ j) не мають спільних точок|спільних|точок|точок|, межа|кордон| кожної клітки|клітини| складається з декількох кривих γі;
ε) кожна з кривих γі служить частиною|часткою| межі|кордону| двох і лише двох кліток|клітин|;
ζ) S = G1 ∪ G2 ∪ … ∪ Gf ∪ γ1 ∪ γ2 ∪ … ∪ γk.
Кожна з кривих γ1, γ2,…, γk | називається ребром кліткового|кліткового| розбиття, кінці ребер — його вершинами. Деякі з кривих γі можуть входити до складу краю поверхні; такі криві γі, звичайно, не повинні фігурувати в правій частині|частці| умови ζ).
Візьмемо будь-який опуклий|випуклий| многогранник і сферу, центр якої лежить усередині многогранника. Спроектувавши всі ребра многогранника на сферу з|із| її центру, ми одержимо|отримаємо| систему сферичних многокутників, які і утворюють кліткове|кліткове| розбиття сфери.
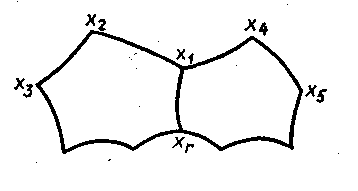
Рис.1. Рис. 2.
Для кожної клітки|клітини| задамо її орієнтацію, тобто порядок|лад| обходу її вершин. Дві сусідні клітки|клітини| вважаються|лічаться| орієнтованими узгоджено|узгоджено|, якщо вони визначають на спільному|спільному| ребрі протилежні напрями|направлення|. Так, на малюнку 1 дві сусідні клітки|клітини| мають орієнтації x1x2…xr i x1xr…x5x4, ці орієнтації узгоджені|погоджені|, оскільки|тому що| для загального|спільного| ребра x1xr маємо в обох клітках|клітинах| протилежні напрями|направлення|.
Поверхня S називається орієнтованою, якщо всі клітки|клітини| її кліткового|кліткового| розбиття можна орієнтувати так, щоб будь-які дві сусідні клітки|клітини| виявилися орієнтованими узгоджено|узгоджено|.
Можна довести, що властивість поверхні S бути орієнтованою топологічно інваріантна; внаслідок цього, якщо одне кліткове|кліткове| розбиття поверхні S орієнтоване, то те ж буде справедливе і для будь-якого іншого її кліткового|кліткового| розбиття.
Узявши яке-небудь кліткове|кліткове| розбиття сфери, можна легко переконатися, що сфера є орієнтована поверхня.
Покажемо, що існують неорієнтовані поверхні. Прикладами|зразками| таких є лист|аркуш| Мебіуса і проективна площина|плоскість|.
Лист|аркушу| Мебіуса по самій його побудові|шикуванню| гомеоморфний| прямокутнику| АВАВ| (мал. 2), у|в,біля| якого ототожнені точки А і А, В і В, Р і Р|із| і т.п. двох протилежних сторін. Показане на малюнку 2 розбиття прямокутника АВАВ| на три клітки|клітини| є|з'являється,являється| його клітковим|клітковим| розбиттям, оскільки|тому що| всі вимоги α), β), ..., ζ), очевидно, виконані. Задамо середній клітці|клітині| орієнтацію KLMN; тоді визначаться узгоджені|погоджені| орієнтації крайніх прямокутників ABLK і NМAВ|. Ребро АВ| в обох крайніх прямокутниках, які на листі|аркуші| Мебіуса будуть сусідніми клітками|клітинами|, орієнтоване однаково від А до В, отже орієнтації виявилися неузгодженими. Неорієнтовність листа|аркуша| Мебіуса встановлена|установлена|.
На проективній площині|плоскості| розглянемо|розгледимо| трьовершинник| ABC (мал. 3). Прямі АВ|, ВС| і |із| СА розбивають всі точки проективної площини|плоскості| на чотири області, які назвемо|накликатимемо| трикутниками. На малюнку 3 трикутник 1 видно повністю, а кожний з решти трикутників 2, 3 і 4 розділений нескінченно віддаленою|віддаленій| прямою на два куски. Орієнтуємо трикутник 1 проти|супроти| годинникової стрілки; тим самим за узгодженням визначаться орієнтації всіх сусідніх трикутників 2, 3, 4, причому їх орієнтації будуть неузгодженими одна з одною: наприклад, сторона АС в обох сусідніх трикутниках 2, 4 напрямлена однаково, від А до С.
мал.3