Построение интервальных оценок

Интервальной называют оценку, которая определяется как интервал с двумя концами (в общем случае случайными), покрывающий оцениваемый параметр.

Интервал , покрывающий оцениваемый параметр, называют интервальной оценкой параметра. Длина интервала зависит от доверительной вероятности ., где - уровень значимости, а также от объема выборки .

Поскольку концы интервала представляют собой случайные величины, то их называют доверительными границами, а сам интервал называют доверительным интервалом.

Интервальная оценка математического ожидания (доверительный интервал) имеет вид:

)

_{Реализация доверительного интервала для математического ожидания имеет вид:}

Для нахождения интервальной оценки математического ожидания на практике необходимо вычислить реализацию точечной оценки математического ожидания

и среднего квадратического отклонения (реализацию стандартного отклонения):

.

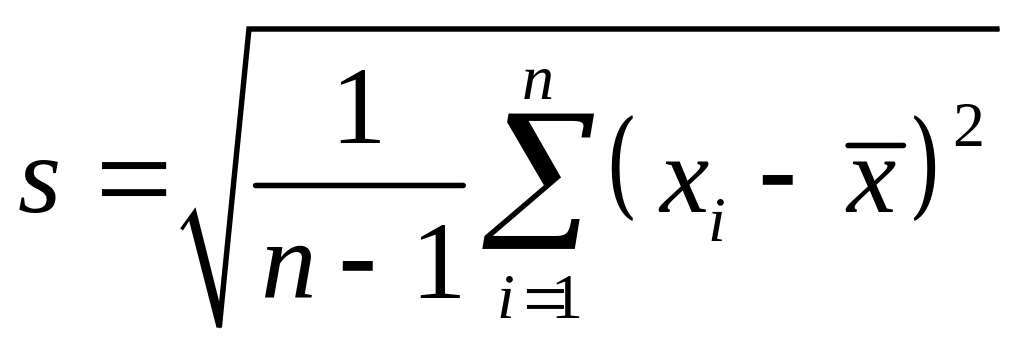Значение параметра t_, находится из таблиц распределения Стьюдента по значениям n и  как решение уравнения:

-вероятность практически достоверного события

-граница практически достоверных значений дроби Стьюдента T_n-1

Границы доверительного интервала для :

=

=

Интервальной оценкой дисперсии служит интервал I_D = ( ₁, ₂),

где 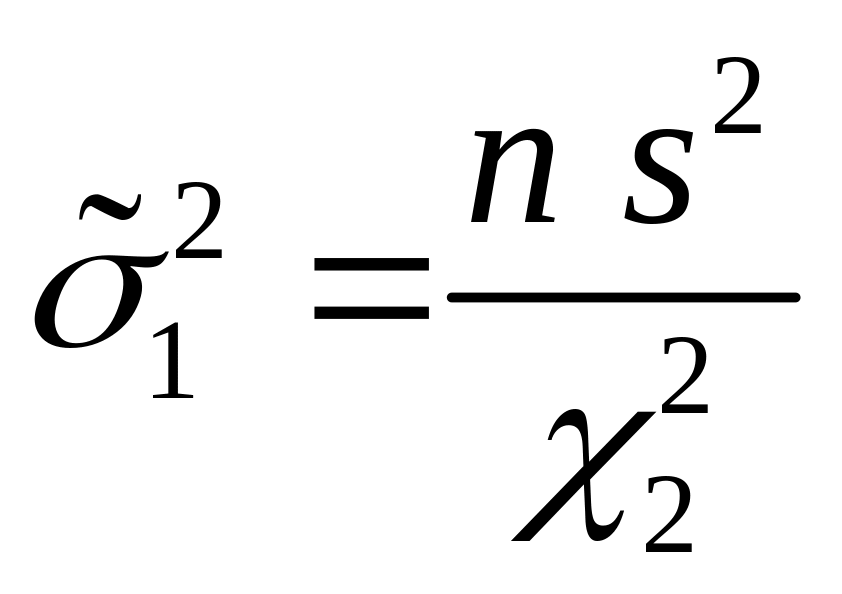, , 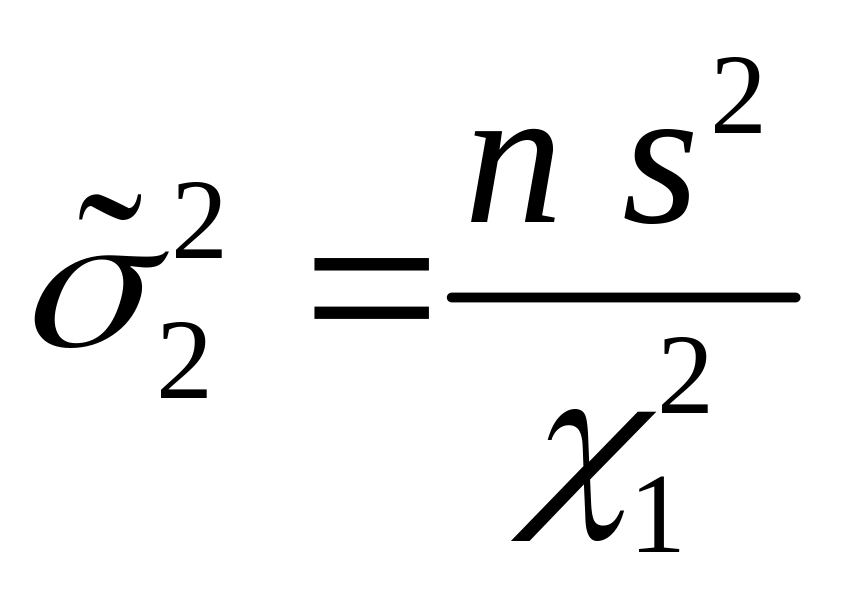значения и находят из таблиц -распределения (Приложение 7) по входам  ₁,  ₂ и числу степеней свободы k=n-1.

Вероятности  ₁ и  ₂ вычисляют по формулам:

 ₁=(1+)/2,

 ₂=(1-)/2.

Здесь – доверительная вероятность, .

Таким образом, интервальная оценка дисперсии – это интервал вида:

( , ).

2.1.5. Построение статистического ряда

Для построения статистического ряда определяют отрезок числовой оси, содержащий все элементы выборки xⁿ=(x₁,…,x_n), т.е. интервал (x_min, х_max). Затем необходимо провести группировку выборки на группы, т. е. интервал (x_min, х_max) разбить на полуинтервалы (разряды). Для этого необходимо разделить точками х⁰,х¹,х²,…,х^q действительную ось на q непересекающихся полуинтервалов (х^j, х^j+1), j= , одинаковой длины.

Количество разрядов вычисляем по формуле: q= , q=5-20, а длину разряда вычисляем по формуле:

l = (х_max – x_min.)/q

Причем x_min = х⁰.

После этого для каждого из разрядов находят представителей разрядов, т.е. устанавливают координаты средних точек разрядов по формуле:

Затем для каждого разряда посчитывают количество элементов вариационного ряда n_j, попавших в разряд (абсолютную частоту разряда), затем вычисляются относительные частоты разрядов:

p^*_j=n_j/n (j= ).

Статистический ряд строится в виде таблицы (см. табл.7).

2.1.5. Построение статистических оценок функции распределения Статистическая оценка функции распределения

Эмпирической (статистической) функцией распределения называют функцию (x), определяющую для каждого значения x относительную частоту события {X x}.

Из теоремы Бернулли следует, что при неограниченном увеличении n относительная частота события Х< х, т.е. (x) стремится по вероятности к F(x) этого события, так как .

Отсюда следует целесообразность использования эмпирической функции распределения выборки для приближенной оценки теоретической функции распределения случайной величины.

Реализация статистической функции распределения F*(x) рассчитывается по формуле:

F*(x) = ,

где число элементов вариационного ряда с учетом кратности, расположенных левее x, (включая текущий элемент x), n – объем выборки.

Пример графика статистической функции распределения представлен на рис.1, из которого видно, что F*(x) представляет собой ступенчатую функцию.

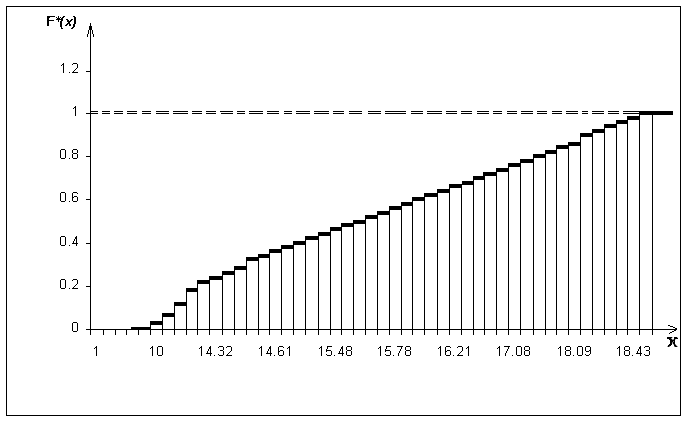
Рис.1. Статистическая функция распределения.

Кумулятивная ломаная

Кумулятивная ломаная является второй оценкой функции распределения.

При достаточно больших объемах выборки измерений (наблюдений) построение на основе всех вариационного ряда ступенчатой оценки F*(x) становится неудобным.

В этом случае для построения оценки функции распределения удобнее использовать данные статистического ряда, а именно:

F**( ) = 0

F**( ) =

F**( ) = +

………………….

F**( ) = = ,

где = 1.

Используя эти формулы, можно построить ломаную F**(x), проходящую через точки ( ), j= и принять ее в качестве второй оценки функции распределения, которая называется кумулятивной ломаной.

Пример расчетов приведен в табл.4.

Номер интервала	1	2	3	4	5	6
Границы интервалов	[14,01; 14.74)	[14.74; 15.58)	[15.58; 16.32)	[16.32; 17.93)	[17.93;18.71)	[18.71; 19.55]
Относительная частота интервалов	0.18	0.16	0.16	0.16	0.16	0.16
F**(x)	0.18	0.34	0.48	0.64	0.84	1

Таблица 4

График кумулятивной ломаной, построенной на основе данных табл.4, представлен на рис.2.

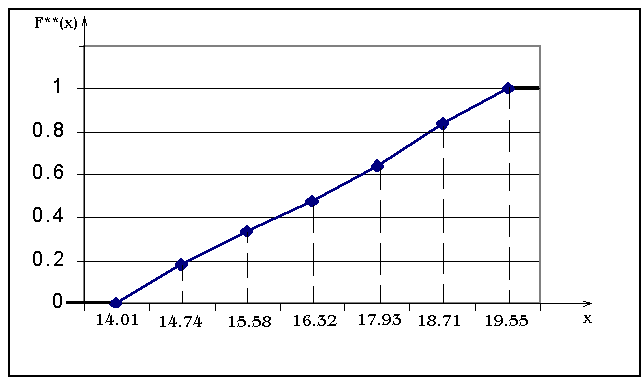
Рис.2. Кумулятивная ломаная