Обнаружение ошибок при циклическом кодировании

Обнаружение ошибок при циклическом кодировании сводится к делению принятой кодовой комбинации на тот же образующий полином, который использовался при кодировании (вид его должен быть известен и на приеме). Если ошибок в приня­той кодовой комбинации нет (или они такие, что данную переда­ваемую кодовую комбинацию превращают в другую разрешен­ную), то деление на образующий полином произведется без ос­татка. Если при делении получится остаток, то это свидетельст­вует о наличии ошибки. Остаток от деления в циклических кодах играет роль синдрома.

Пример

Пусть при приеме получена кодовая комбинация 1111010, вместо посланной разрешенной комбинации 0111010, т.е. в информационной части произошла ошибка в старшем (7-м) разряде (раз­ряды считаем справа налево). Известно, что образующий полином имеет вид: P(x)=x³+x+1.

Требуется обнаружить ошибку.

Для обнаружения ошибки запишем полученную кодовую комбинацию в виде полинома 1111010 → x⁶+x⁵+x⁴+x³+x. Разделим полученный полином на известный образующий полином. Имеем:

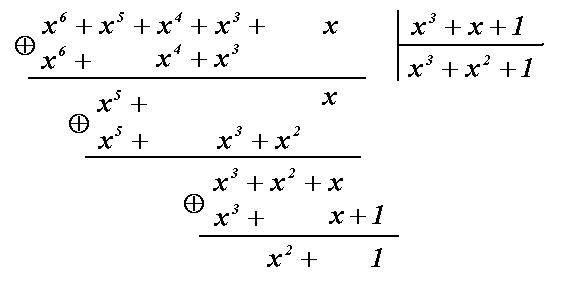
Наличие остатка R(x)=x²+1 свидетельствует об ошибке.

Определение места ошибки. Выбор образующего полинома

Остаток от деления R(x) - синдром циклического кода. Если синдром не равен нулю, то это свидетельствует о наличии ошибки. В кодах с образую­щим полиномом степени r остаток представляется в виде полинома, степень которого меньше r. Это означает, что количество раз­личных ненулевых остатков может быть равным 2^r -1. Если номер разряда, в котором произошла ошибка, однозначно связать с видом получаю­щегося при этом ненулевого остатка, то можно определить не только наличие ошибки, но и ее место и исправить ошибку.

Таким образом, для исправления ошибок необходимо обеспе­чить условие, при котором количество различных ненулевых ос­татков будет равно количеству элементов n (при исправлении од­ной ошибки) или числу комбинаций из n по t_и, где t_и — количест­во ошибок (кратность), исправляемых кодом.

Пример

Имеется кодовая комбинация циклического кода содержащая 15 элементов (n=15). Код исправляет двукратные ошибки (t_и=2). Определить число проверочных элементов кодовой комбинации и вид примененного кода.

Определим возможное число двукратных ошибок в кодовой комбинации, состоящей из 15 элементов. Очевидно, что ошибки могут быть

в 1,2; 1,3; …2,3; 2,4 … и т.д. разрядах. Т.е. общее число возможных ошибок определяется по формуле сочетаний из 15 элементов по 2:

Т.о. необходимо выбрать образующий полином обеспечивающий 105 различных остатков, или

2^r -1≥105, откуда получаем r=7 (2⁷-1 = 127).

Следовательно, комбинация имеет 7 проверочных разрядов, для кодирования нужно вы­брать образующий многочлен с r=7 и код (15,7).

Не все неприводимые многочлены по­зволяют формировать 2^r-1 различных остатков. Это присуще только определенному подклассу неприводимых многочленов. Такие многочлены называются примитивными.

Поэтому в качестве образующих многочленов используют примитивные многочлены. Их признаком является наличие остатка, равного единице только при делении на них х⁰ (т.е. 1) и хⁿ, где n — количество элементов в кодовой комбинации. Между n и r для таких полиномов имеется зависимость 2^r=n-1. Здесь n - максимальное количество элементов, при котором число различающих­ся ненулевых остатков равно n-1. Поэтому в таблицах образующих полино­мов указываются только примитивные полиномы.

Для определения места ошибки в циклическом коде существу­ет несколько методов, основанных на анализе синдрома R(x). Рассмотрим один из них.

Принятую кодовую комбинацию F'(x) можно представить в виде F'(х)=F(х) E(x),

где Е(х) - многочлен ошибки,

F(x) – переданная кодовая комбинация.

Например, ес­ли F(0,1)=01110111, а E(0,1) = 10000000, то F´(0,1) =11110111 (здесь комбинации записаны в виде двоичных кодов, поэтому аргументы F и E нуль и единица).

Остаток от деления принятой кодовой комбинации F'_n(x) на Р(х) равен остатку от деления на Р(х) кодовой комбинации ошибки Е_n(х), если

где n – число элементов кодовой комбинации.

Это действительно так, учитывая, что F_n(x) разрешенная кодовая комбинация, которая делится на P(x) без остатка, но тогда и суммарный остаток от деления на P(x) многочленов F'_n(x) и Е_n(х) должен быть равен нулю. А это выполняется, если эти остатки равны, тогда их сумма по модулю 2 будет равна нулю.

Пример

Имеется циклический код (11,7). Передана разрешенная комбинация F₁₁(0,1)=10110111100. Принята кодовая комбинация F'₁₁(0,1)=00110111100.Требуется найти кодовую комбинацию ошибки Е(0,1). Убедиться, что остатки от деления F'₁₁(0,1) и Е(0,1) на образующий полином равны. Образующий полином имеет вид Р(0,1)=10011.

Т.к. F'(х)=F(х) E(x), то многочлен ошибки равен (учитывая, что операции вычитания и сложения по модулю 2 совпадают):

Для примера все операции будем выполнять над двоичными числами, а не над многочленами, тогда:

Комбинация ошибки показывает, что в принятой кодовой комбинации имеется одна ошибка в старшем разряде.

Найдем остаток от деления принятой кодовой комбинации F'₁₁(0,1)на P(x):

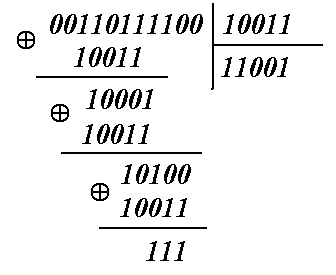
Найдем остаток от деления комбинации ошибки E(0,1)на P(x):

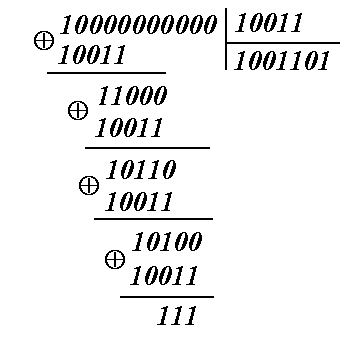
Сравнение остатков показывает, что для обоих случаев они одинаковы.

Это свойство позволяет сделать вывод, что синдром не за­висит от переданной кодовой комбинации, а определяется лишь наличием ошибок. Указанное свойство можно использовать для определения ошибочно принятого элемента.

Алгоритм определения места ошибочно принятого элемента следующий:

1. Записывается многочлен ошибки (или кодовая комбинация, если вычисления выполняются над двоичными числами) соответствующий ошибке в старшем разряде кода.

2. Многочлен ошибки делится на образующий полином, находится остаток R₀. Этот остаток является синдромом ошибки в старшем разряде.

3. Полученная кодовая комбинация F'_n делится на образующий полином, находится остаток R₁.

а) Если R₁ =0, комбинация принята без ошибок.

б) Если R₁ = R₀, принятая комбинация имеет ошибку в старшем разряде.

в) Если R₁ ≠ R₀, к принятой комбинации дописывают 0 справа и продолжают деление.

4. Пункт 3в) повторяют до тех пор, пока полученный при делении остаток R_i станет равен R₀ (R_i = R₀). Позиция ошибочно принятого разряда равна числу приписанных к кодовой комбинации нулей плюс 1. Позиции в кодовой комбинации считаются слева направо.

Замечание: приписывание нуля к кодовой комбинации эквивалентно ее сдвигу на одну позицию влево. Когда ошибочно принятый разряд в результате таких сдвигов попадет на позицию старшего разряда, выполнится условие R_i = R₀.

Пример

При пользовании циклического кода (11,7) была принята комбинация F'₁₁(0,1)=10111111100. Определить наличие ошибки и исправить ее, если известно, что используемый код исправляет одну ошибку, образующий многочлен имеет вид Р(0,1)=10011.

Все операции будем выполнять над двоичными числами.

1. Запишем кодовую комбинацию ошибки, соответствующую ошибке в старшем разряде кода (учитываем, что n=11):

2. Многочлен ошибки разделим на образующий полином и найдем остаток R₀. Из предыдущего примера R₀=111.

3. Полученную кодовую комбинацию F'₁₁(0,1) делим на образующий полином:

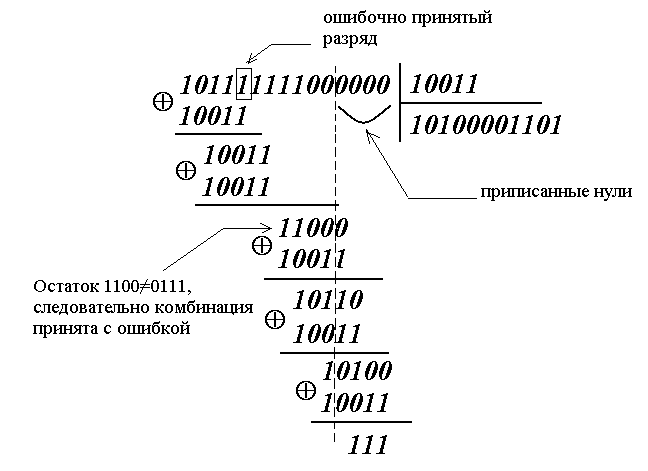
Остаток от деления стал равен остатку R₀=111после приписывания четырех нулей. Следовательно, ошибочно принят разряд на 5-ой позиции, если считать слева направо. Верная комбинация имеет вид: 10110111100.